杨伍梅，刘 权

(1.益阳职业技术学院， 湖南 益阳 413049; 2.湖南益阳电厂， 湖南 益阳 413000)

0 前言

随着计算机的广泛应用，在科学研究、经济管理和工程设计等许多领域中，常常会遇到怎样使成本最低、利润最大等最优化问题.在数学上往往将这类问题在合理假设下建立相应模型，将之转化为无约束优化问题:minf(x)，x ∈Rn的求解.而拟牛顿法是目前求解无约束优化问题的最成熟，应用最广泛的方法之一，它具有收敛速度快与数值效果好等优点.最常见的拟牛顿法有Broyden 族秩1 校正(R1)法［1］，对称秩1 法(SR1)［1］，BFGS 法［2］，DFP 法［3］，PSB 法［4］.本文就无约束优化问题采用对称秩1 法和BFGS 法进行探讨.

1 两种方法的比较

1.1 对称秩1 法

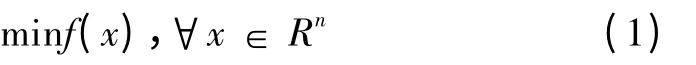
设目标函数f ∶Rn→R 连续可微，无约束优化问题的基本形式为［3］:对称秩1 法的主要思想是用一个秩 1 矩阵:去校正拟牛顿矩阵，使得所产生的矩阵:

满足拟牛顿方程Bk+1sk= yk.其中sk= xk+1－xk，yk= gk+1－ gk.显然因为其修正矩阵的秩为1，所以矩阵Bk更新很简单;对所有的k，只要初始矩阵B0对称正定，必有Bk对称正定;且Bk≈2f(xk)，因而可使算法产生的方向近似于牛顿方向，算法具有较快的收敛速度［3］.

对称秩1 算法的一般计算步骤如下:

步1 给定点x0∈Rn，终止误差0 ＜ε＜1，初始对称矩阵B0= I，令k ∶= 0.

步2 若‖gk‖ε，则算法终止，输出xk作为近似极小点.

步3 由方程Bkdk+ g(xk)= 0 计算搜索方向dk.

步4 用线性搜索技术求步长因子αk.

步5 令xk+1= xk+αkdk，由对称秩1 公式(2)确定Bk+1.

步6 令k ∶= k +1，转步2.

下面给出Armijor 线性搜索［3］下的对称秩1 算法的程序.

程序1 (对称秩1 算法程序)

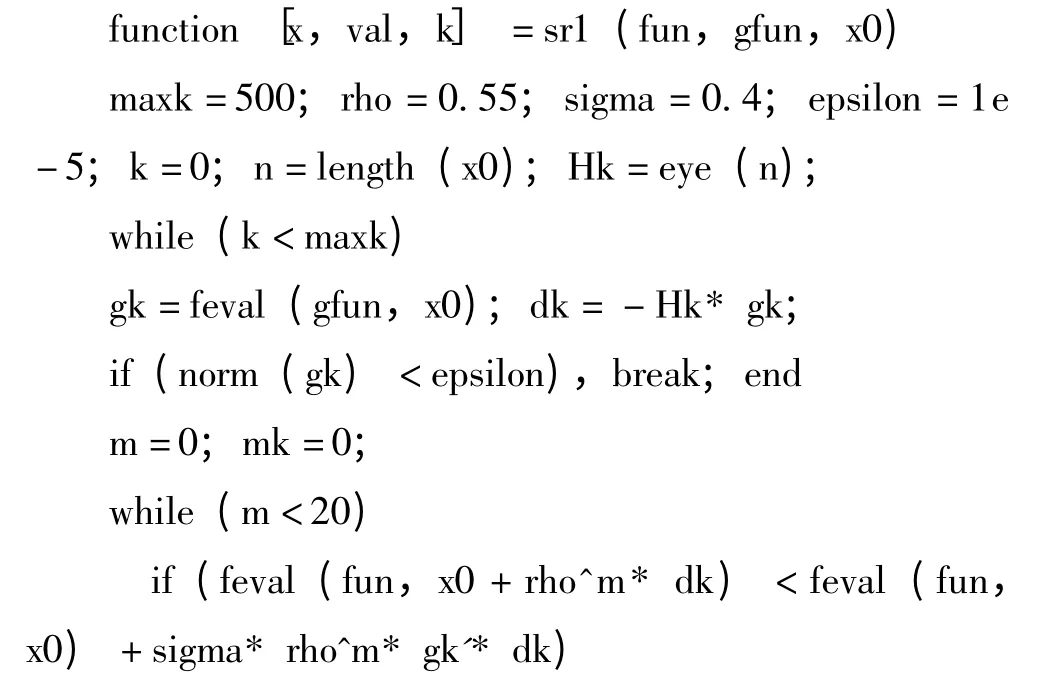
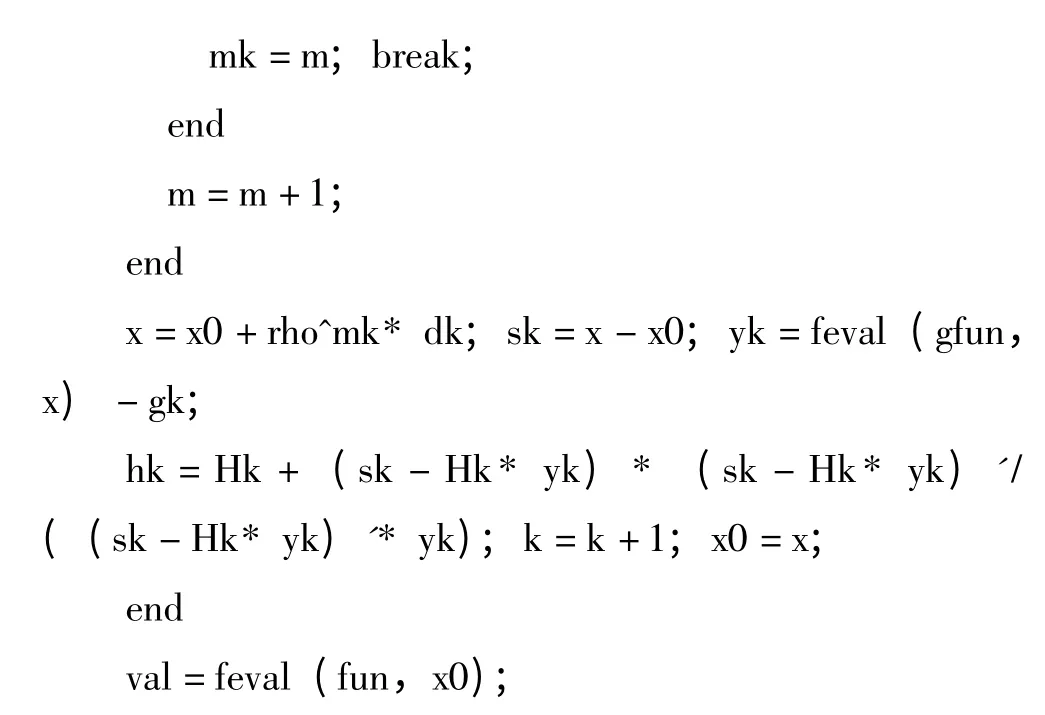
1.2 BFGS 算法

BFGS 算法是拟Newton 算法中最有效的方法之一［6］，它是由Broyden、Fletcher、Goldfarb 和Shanno 四人在1970年各自独立提出的.其思想、步骤与对称秩1 算法的步骤类似，只需将矩阵迭代公式(2)换成:

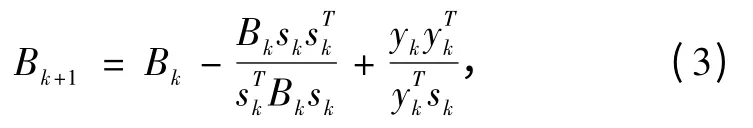
而且由理论可知，在Armijor 搜索准则下一般不能保证的矩阵序列{Bk}的对称正定性.但Armijor 搜索准则因其简单且易于程序实现深得人们的喜爱，因此，为了保证采用Armijor 搜索准则时矩阵序列{Bk}的对称正定性，可采用如下的校正方式:

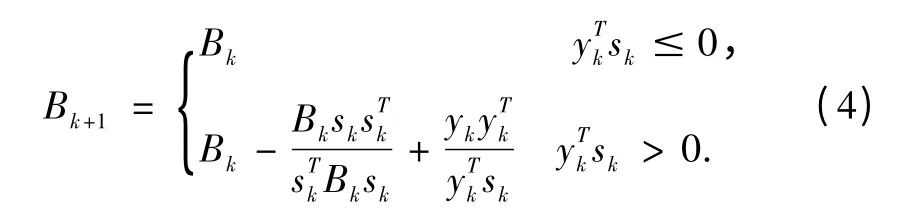
不难发现，只要B0对称正定，上述校正公式可以保证矩阵序列{Bk}的对称正定性，利用公式(4)产生的Hessian 矩阵的近似，避免了直接计算Hessian 矩阵的麻烦，从而具有快速的收敛性和较好的数值效果［6］，它已成为人们解决最优化问题的一类最受欢迎的方法

.

下面给出Armijor 线性搜索下BFGS 算法的步骤［7］:

步1 给定参数δ ∈(0，1)，σ ∈(0，0．5)，初始点x0∈Rn，终止误差0 ε ＜＜1.初始对称矩阵B0= I，令k ∶= 0.

步2 若‖gk‖ε，则算法终止，输出xk作为近似极小点.

步3 由方程组Bkdk+g(xk)= 0 计算搜索方向dk.

步4 设mk为满足的最小非负整数m，令αk= δmk，

步5 令xk+1= xk+ αkdk，由(4)式确定矩阵Bk+1;

步6 令k ∶= k +1，转步2.

Armijor 线性搜索下的BFGS 算法［8］的MATLAB 程序如下:

程序2 (BFGS 算法程序)

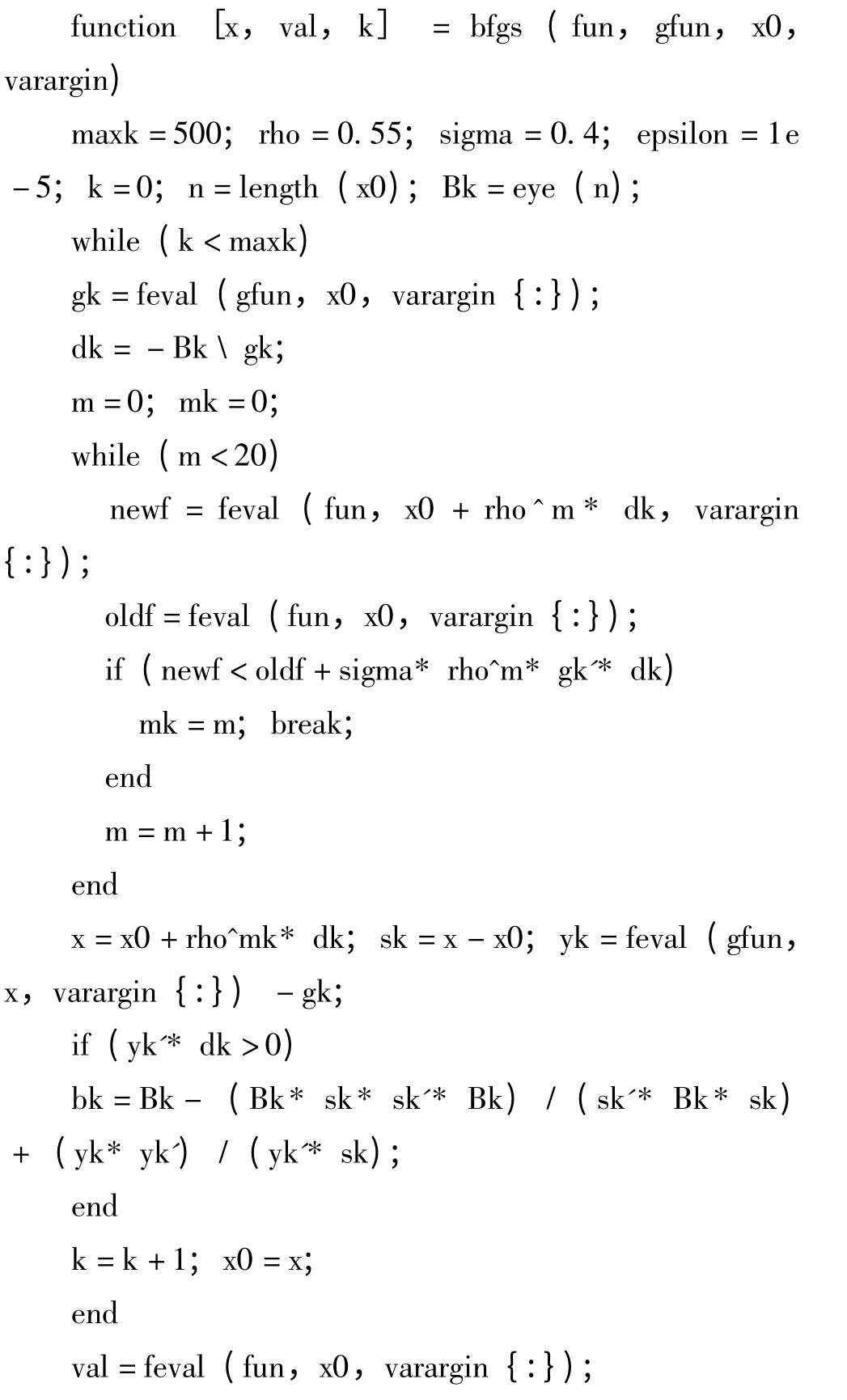
2 无约束优化问题在matlab 中的实现

利用程序1 和程序2 求解无约束优化问题［9］:

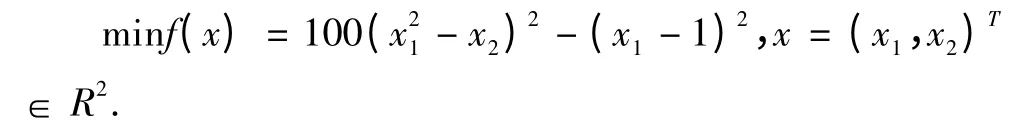
该问题有精确解x*= (1，1)T，f(x*)= 0．

对于实例1，采用MATLAB 编写程序，在带有1.80GHZ 的CPU 处理器，1.00GB 内存的个人电脑上实现.表1 列出对了称秩－1 法与BFGS 法计算实例1的数值结果，其中初始点为x1= (0，0)T，x2= (0．5，0．5)T，x3= (2，2)T，x4= (－1，－1)T，x5= (1，10)T，x6=(10，10)T.表中“init”为初始点，“k”为总的迭代次数，“f(xk)”为目标函数值，“total”为总数，“average”为平均数.

表1 对称秩1 法与BFGS 法的数值比较

从表1 的数据中不难发现，在相同的初始条件和线性搜索下BFGS 法的平均迭代次数为60.666 次，而对称秩1 法的平均迭代次数为32 次，可以发现BFGS法的平均迭代次数比对称秩1 法减少约28.666 次;且当初始点离精确解较近时，两种方法的秩代次数相差不大，当初始点离精确解较远时，对称秩1 法所用的秩代次数将是BFGS 法的两倍还多，这在很大程度上影响了求解速度.从精确度而言两种方法所求得的值都在10－11以上，都达到很高的精度，没有太大的差别.由此可知，对于无约束优化问题的求解BFGS 法优势更明显.

3 结论

本文主要针对无约束优化问题，对对称秩1 法与BFGS 法进行了探讨，并编写了两种方法的matlab 程序，通过对实例进行求解，由其数值结果分析出BFGS算法比对称秩－1 法更为有效;且用MATLAB 编程来计算无约束优化问题，结果可靠，计算精度高，是一个值得推广的方法.对于两种方法求解实例时只给出了秩代次数和精确度的数据比较，以后还可从计算时间上进行数据比较.

［1］Broyden C G．A class of methods for solving nonlinear simultaneous equations［J］．Math．Compu．，1965，19:577－593．

［2］Dennis J E，Moré J J．A characterization of superlinear convergence and its application to quasi－ Newton methods［J］．Math．Compu．，1974，28:549－560．

［3］Dennis J E．Toward a unified convergence theory for Newton－like methods，in:L．B．Rall， (Eds．)，Nonlinear functional analysis and applications［J］．Academic press，NewYork，London，1971:425－472．

［4］陈兰平，焦宝聪．非凸无约束优化问题的广义拟牛顿法的全局收敛性［J］．应用数学，2005 (18):573－579．

［5］李董辉，童小娇，万中．数值最优化算法与理论［M］．北京:科学出版社，2010．

［6］刘陶文．BFGS 方法及其在求解约束优化问题中的应用［D］．长沙:湖南大学，2006:7－12．

［7］马昌凤．最优化方法及其MATLAB 程序设计［M］．北京:科学出版社，2010．

［8］李明．详解MATLAB 在最优化计算中的应用［M］．北京:电子工业出版社，2011．

［9］沈欢．用Newton 法、DFP 方法和BFGS 方法求解函数极值［D］．北京:北京大学工学学院，2011．

［10］刘敬华．无约束向量集值优化中的二次最优性条件［J］．怀化学院学报，2007 (11):30－33．