张学敏　钟菲

摘 要：音频信号瞬态段检测技术是数字音频编码的关键技术之一，它的优劣直接影响后续编码过程的复杂度及编码质量。针对平坦测量检测方法中存在冗余检测的不足之处，该文介绍了方差-平坦测量综合瞬态段检测方法，并对音频样本在MATLAB环境下进行了仿真测试，结果证明，该算法提高了音频信号瞬态段检测的时间分辨率，减少瞬态段的冗余检测，同时能检测其发生的位置，为瞬态信号的处理提供判断依据。

关键词：方差 平坦测量 瞬态检测 MATLAB

中图分类号：TN911 文献标识码：A 文章编号：1672-3791（2015）07（c）-0022-02

现有音频编码器是基于心理声学模型、利用人耳的掩蔽效应对原始音乐信号进行压缩，如果音频编码器的时频变换块太长，会导致量化噪声在整个块中扩散，人耳能明显感知的噪声的存在，即通常所说的预回声现象[2]。

解决预回声问题的方法以瞬态信号检测为前提，主要有：比特池方法、长短块切换、混合滤波器组等。这些方法在算法复杂度，准确度（漏检和误检）上存在不足。该文提出的方差-平坦测量综合检测技术可以弥补现有瞬态检测方法的不足，在一定程度上提高了音频信号瞬态段检测时间分辨率，具有检测准确度高、算法简单的优点。

1 瞬态信号的特点

信号的瞬变现象和不规则结构（如信号波形的跃变、间断、快速振荡等）常常携带着信号的大部分信息，包含这种瞬变现象和不规则结构的信号，一般称为瞬态信号[3]。根据时域-频域的对偶性可知，时域较平坦的信号，频谱则不平坦；时域不平坦的信号，频谱则较平坦。例如正余弦信号在频域呈尖锋状，而脉冲信号的频谱在频域却是呈均匀分布的。因此，时域上越不平坦、频域上越平坦的信号，就越接近于瞬态信号；相反，就越接近于平稳信号。

2 方差-平坦测量综合瞬态段检测方法

造成多余检测主要原因是当整帧信号的样本差波动很大时会被误检测为瞬态信号。然而对于样本差来说，当前帧的样本差值相对来说比较小，可以设置适当阈值将多余检测消除。

方差是对一组样本数据平均值分散程度的度量。方差越大，单个样本和其平均值之间差异越大；反之，单个样本值就越接近平均值。

设表示当前块中的第个样本值，是的绝对值，为当前块中的样值总数，代表当前块中样本的平均值。表达式为：

平坦测量算法中，重要的还是判决门限的确定上，门限值的大小直接影响着瞬态段信号检测的准确性。根据信号段中瞬态的强弱，平坦测量算法利用3 种门限来判断信号段的瞬态性。此算法主要分时域平坦测量（）和频域平坦测量（）两部分。若信号的瞬态强度较大，当时域平坦测量大于门限值时，判定此信号段为瞬态段，相反，判定此信号为稳态段；当频域平坦测量小于门限值时，判定此信号段为瞬态段，相反，判定此信号段为稳态段。若瞬态强度不较明显，则根据和确定时频综合的判决指标和门限值，比较和的大小来确定是否是瞬态信号。由于同一信号的和是往相反方向变化的，因此可定义为[2]：

其中为很小的正常数。越小信号越类似瞬态的；相反，则信号越类似平稳的。基于方差-平坦测量的瞬态检测算法原理框图如图1所示。

3 仿真测试结果

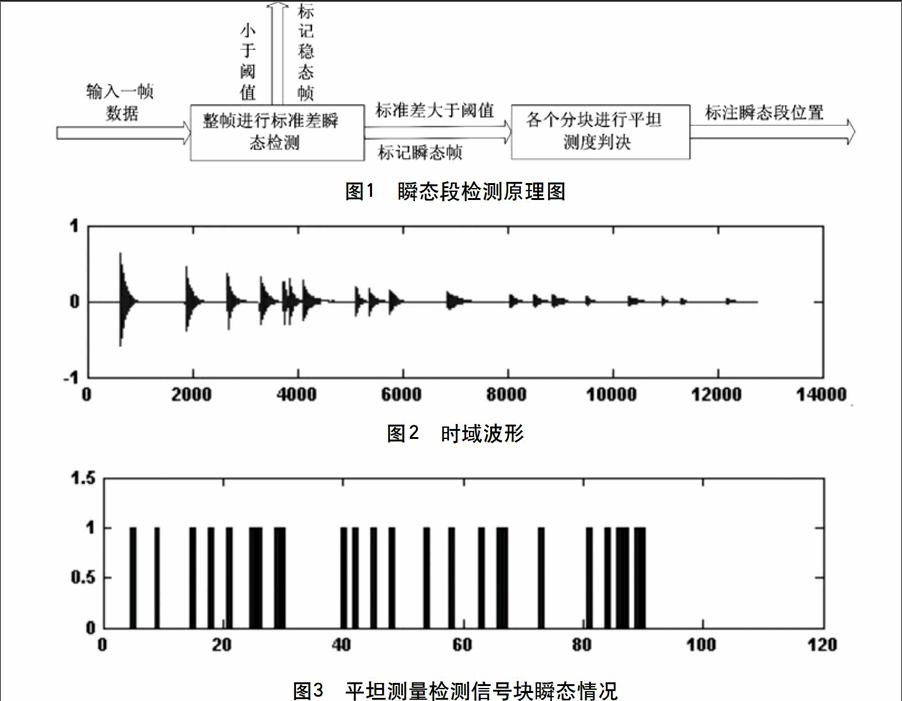
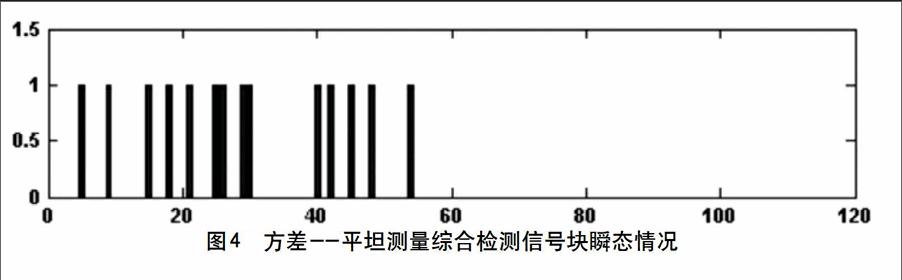
利用方差-平坦测量综合方法对信号做瞬态检测，并在MATLAB环境下以MATLAB自带音频信号smlsplas.wav做仿真测试，测试信号的时域波形见图2。用平坦测量的方法做瞬态段检测结果见图3，用方差-平坦测量综合的方法检检测结果见图4。通过对比分析图3和图4易见，综合方法弥补了平坦测量在瞬态检测上的不足，有效减少了冗余检测，并能检测瞬态信号发生的位置。

4 结语

通过上面的仿真结果可以得出，该文所提出的方差-平坦测量综合检测方法，与单独用平坦测量检测方法相比，在瞬态段上几乎不产生多余检测。由于音频信号随机性比较强，不同的音频信号在特性上差别比较大。因此方差-平坦测量综合检测方法并不能保证对每一个音频信号中瞬态段都能准确检测，这是它的不足之处。

参考文献

[1] 杨振，邹男，付进.Hilbert-Huang变换在瞬态信号检测中的应用[J].声学技术，2015，34（2）：167-171.

[2] 周延献，张涛，王赞.基于方差-平坦测度的音频瞬态段检测算法[J].电声技术，2012，36（2）：64-66.

[3] 张涛，周延献，张瑞生，等.基于方差的音频信号瞬态段检测方法：中国，201110219767.X[S].2011-8-02.

[4] 王永军，史捷，张旭，等.滤波补偿方法及其在瞬态检测中的应用[J].控制与决策，2015，15（6）：740-743.