蔡南莲

(集美大学理学院,福建厦门361021)

具有相依变量成批到达排队系统等待时间的注记

蔡南莲

(集美大学理学院,福建厦门361021)

研究了成批到达排队系统G(X)/G/1的基本变量具有相依关系时,等待时间的随机比较性质.证明了当到达批量与到达间隔的相依关系越强时,相应的等待时间越短;当服务时间和到达间隔的相依关系越强时,相应的等待时间越短.同时探讨了基本变量相依时成批到达排队系统的等待时间的界.

正象限相依;上模序;增凸序;Frëchet界;成批到达排队系统;等待时间

单个服务员的成批到达排队系统G(X)/G/1是运筹学中很重要的数学模型.研究问题时通常假设基本变量之间是相互独立的.如在文献[1-2]中,研究了成批排队系统M(X)/G(Y)/1的队长的性质,当2个成批排队系统M(X)/G(Y)/1的基本变量满足随机序(增凸序)关系时,得出了成批排队系统的队长也满足随机序(增凸序)关系;文献[3]探讨了成批到达排队系统的顾客的等待时间的随机比较性质,当2个这样的系统的基本变量满足一定随机序、凸序关系时,得出了顾客的等待时间的随机序、凸序关系性质.

在实际应用中,成批到达排队系统G(X)/G/1的基本变量间的相互独立性的假设常常有局限性.众所周知,如果到达批量较大或者顾客的服务时间较长时,下一个顾客更可能会“知难而退”,在这种情况下,是顾客的到达批量与顾客的到达间隔有相依关系,顾客的服务时间与顾客的到达间隔也有相依关系的一个例子.因此,基本变量之间的相依关系对排队系统的队长、等待时间和忙期等排队系统的重要指标的影响的研究具有实际意义和应用价值.近年来,对具有相依变量的排队系统的研究日益得到重视.如在文献[4]中,通过模拟得出,对于M/M/1排队系统,顾客的等待时间随着顾客的服务时间与顾客的到达时间的相关程度而下降;文献[5]中,假设G/G/1排队系统中顾客的服务时间与接下来的顾客到达时间有相依关系时,研究对G/G/1系统的等待时间的影响;Cai等[6]在文献[1-2]的基础上,探讨了在成批排队系统M(X)/ G(Y)/1(G(X)/M(Y)/1)中,当顾客的服务时间与顾客的服务批量(顾客的到达间隔与顾客的到达批量)之间有相依关系时,排队系统的基本随机变量满足一定的随机序关系时,排队系统的队长的随机序性质.

本文考虑成批到达排队系统G(X)/G/1,分别在(i)顾客的到达批量与顾客的到达间隔相依;(ii)顾客的服务时间与顾客的到达间隔相依两种情形下,当系统的基本变量满足一定的随机序关系时,探讨系统的等待时间的性质.该研究结果可看成是文献[3]中考虑的基本变量独立到基本变量相依的进一步结论,也可看成是文献[5]中考虑的G/G/1系统到G(X)/G/1系统的补充.

1 随机序、相依的概念及引理

首先回顾一下随机序、相依的概念(有关更详细的内容可参见文献[7]),及要用到的一些引理.

定义1 (i)二维随机向量X=(X1,X2)称为PQD(positive quadrant dependence),如果对任意的x1,x2∈R,P(X1≤x1,X2≤x2)≥P(X1≤x1)P(X2≤x2).

(ii)设X=(X1,X2)和Y=(Y1,Y2)是二维随机向量,称X≤cY,如果对任意的x1,x2∈R,P(X1≤x1, X2≤x2)≤P(Y1≤x1,Y2≤x2).

定义2 (i)二元函数f(x,y)称为上模的,如果对任意的x1,x2∈R,ε,δ＞0,有f(x1+ε,x2+δ)-f(x1+ε,x2)-f(x1,x2+δ)+f(x1,x2)≥0.

(ii)设X=(X1,X2)和Y=(Y1,Y2)是2个二维随机向量,称X依上模序小于Y(记为X≤smY),如果Ef(X)≤Ef(Y)对所有使得积分存在的上模函数均成立.

(iii)设X和Y是2个随机变量,称X依增凸序序小于Y(记为X≤icxY),如果Ef(X)≤Ef(Y)对所有使得积分存在的增凸函数均成立.

容易得出,当X=(X1,X2)和Y=(Y1,Y2)有相同的边际分布时,下列命题成立:

(i)如果X是PQD且Y1与Y2独立时,有Y≤cX.

(ii)设X≤cY,则X≤smY(见文献[8]定理2.5).

下面介绍一些引理.

引理1[6]设Y1,Y2,ξi,i=1,2,…是非负的随机变量,N,M是取正整值的随机变量.如果(N,Y1)≤sm(M, Y2),则ξ1+…+ξM-Y2≤icxξ1+…+ξN-Y1.

(ii)设随机变量X,Y满足X≤icxY,且f(x)是增凸函数,则f(X)≤cf(Y).

引理3[5]设X=(X1,X2)和Y=(Y1,Y2)是二维随机向量,X≤icxY,则Y1-Y2≤icxX1-X2.

引理4 设v1k,v2k(k=1,2,…),u1,u2是非负随机变量,(v11,u1)≤sm(v21,u2),(v12,…,v1k)与(v22,…,v2k)同分布,(vi1,ui)与(vi2,…,vik)相互独立,i= 1,2.则

因为(vi1,ui)与(vi2,…,vik)相互独立,i=1,2,则对任意的上模函数f(x,y)和t2,…,tk≥0,由式(1)得:

由于(v12,…,v1k)与(v22,…,v2k)同分布,所以

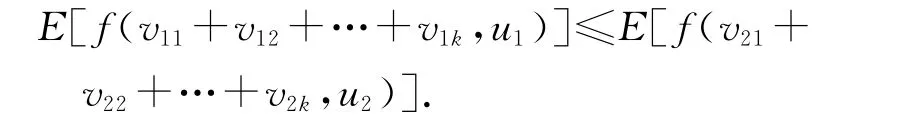
此即(v11+v12+…+v1k,u1)≤sm(v21+v22+…+v2k, u2).

引理5[2]函数f(x)是实凸函数当且仅当对任意的实数a＞0,f(x+a)-f(x)关于x是增函数.

2 到达批量与到达间隔相依的情形

顾客的到达批量与顾客的到达间隔有相依关系的成批到达排队模型G(X)/G/1描述如下:

(i)顾客在时刻0=t0,t1,t2,…到达,到达批量分别为X1,X2,X3,…,到达间隔时间为un=tn-tn-1.设(Xn,n≥1),(un,n≥1)分别是相互独立同分布随机变量序列,在时刻tn-1到达的顾客称为第n批到达的顾客.

(ii)第n批到达的顾客随机地接受服务,设第k个接受服务的顾客的服务时间为vnk,n=1,2,…,k= 1,2,…,Xn.设(vnk,n,k=1,2,…)相互独立同分布.

(iii)设随机向量序列{(Xn,un),n≥1}相互独立同分布.即仅允许第n批的到达批量Xn与下一批顾客的到达间隔un有相依关系,但第n批的到达批量Xn与其他批的到达间隔uk(k≠n)是相互独立的.

(iv)设随机过程{(Xn,un),n≥1}与(vnk,n,k=1, 2,…)相互独立.

满足(i)～(iv)的成批到达排队系统G(X)/G/1称为具有特征[(Xn,un),vnk].

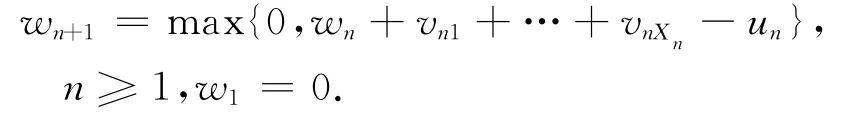
对于上面的模型,有下面的结论.

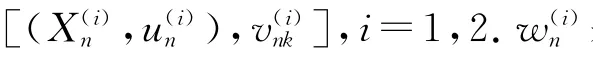
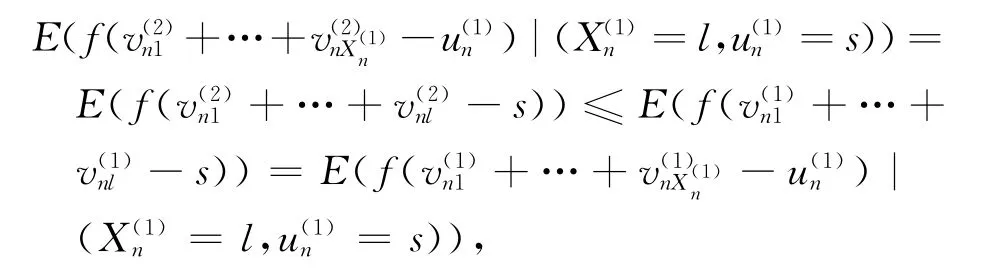
其中不等式成立利用了引理2.

从而

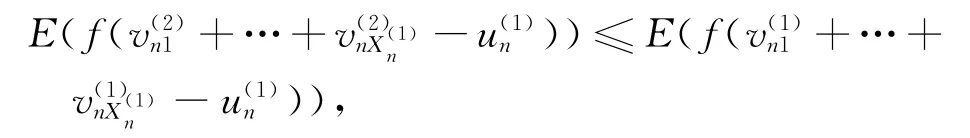
即

由式(2),(3)得

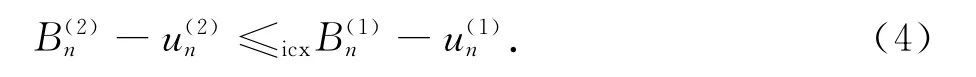
下面利用数学归纳法可以证明命题.

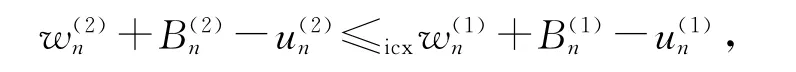
3 服务时间与到达间隔相依的情形

顾客的服务时间与顾客的到达间隔有相依关系的成批到达排队模型G(X)/G/1.描述如下.

(i)顾客在时刻0=t0,t1,t2,…到达,到达批量分别为X1,X2,X3,…,到达间隔时间为un=tn-tn-1.设(Xn,n≥1),(un,n≥1)分别是相互独立同分布随机变量序列,在时刻tn-1到达的顾客称为第n批到达的顾客.

(ii)第n批到达的顾客随机地接受服务,设第k个接受服务的顾客的服务时间为vnk,n=1,2,…,k= 1,2,…,Xn.设(vnk,n,k=1,2,…)相互独立同分布.

(iii)设随机向量序列{(vn1,un),n≥1}相互独立同分布.即仅允许第n批到达第一个接受服务的顾客的服务时间vn1与下一批顾客的到达间隔un有相依关系,但第n批到达第一个接受服务的顾客的服务时间vn1与其他批的到达间隔uk(k≠n)是相互独立的.

(iv)设随机过程{(vn1,un),n≥1},{Xn,n≥1}与(vnk,n≥1,k≥2)相互独立.

满足(i)～(iv)的成批到达排队系统G(X)/G/1称为具有特征[Xn,(vnk,un)].

令wn表示第n批到达第一个接受服务的顾客的等待时间,则有下列循环关系式:

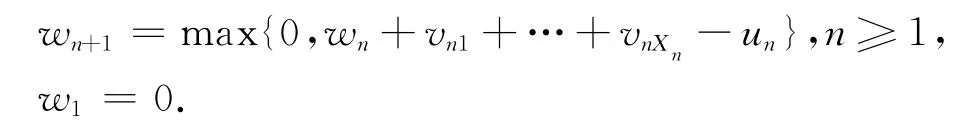
对于上面的模型,有下面的结论.

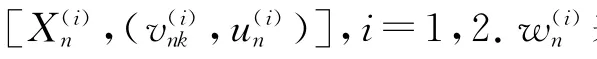
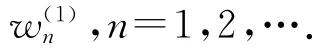
利用引理3得:

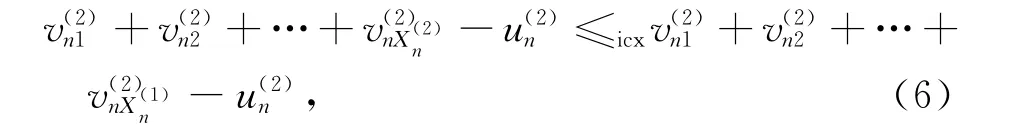
接下来,可以证明下面的不等式:

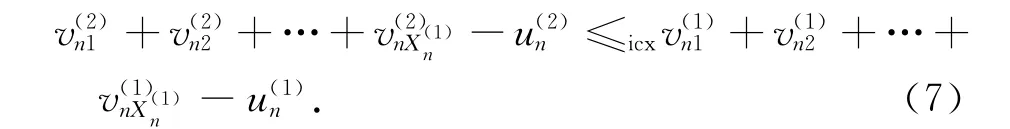
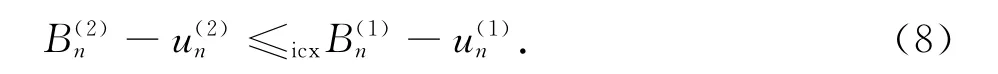
利用数学归纳法可以证明余下的部分,与定理1类似,略去.

4 等待时间的界

利用定理1和定理2,可以得到到达批量与到达间隔相依,服务时间与到达间隔相依两种情形下的成批到达排队系统的顾客等待时间的界,下面给出例子.

例1 设Σ表示到达批量与到达间隔相依具有特征[(Xn,un),vnk]的成批到达排队模型,wn表示第n批到达第一个接受服务的顾客的等待时间.设(Xn, un)具有联合分布函数(二维Pareto分布[9]),

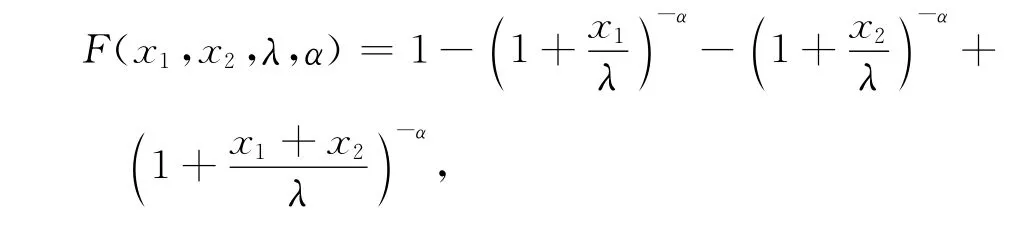
λ,α＞0,x1,x2＞0.

固定α＞0,则F(x1,x2,λ,α)关于λ单调下降.

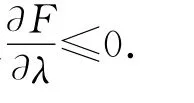
即(Xn,un)在≤c序意义下关于λ单调下降.

所以利用定理1,wn在增凸序的意义下关于λ单调增加.

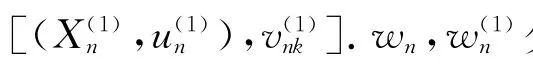
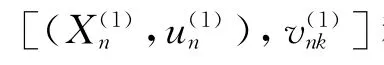
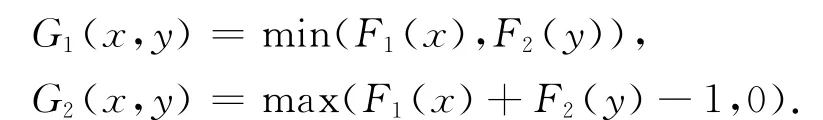
[1] Prabhu N U.Stochastic comparison for bulk queue[J]. Queueing System,1987(1):265-277.

[2] 蔡南莲,肖必泉,郑耀辉.成批排队系统的随机比较[J].运筹学杂志,1994,13(2):59-65.

[3] 蔡南莲.成批到达排队系统等待时间的随机比较[J].厦门大学学报:自然科学版,1999,38(5):661-663

[4] Mitchell C R,Paulson A S.M/M/1-queues with inter-dependent arrival and service processes[J].Naval Research Logistics Quarterly,1979,40:467-475.

[5] Müller A.On the waiting times in queues with dependence between interarrival andservice times[J].Operations Research Letters,2000,26:43-47.

[6] Cai N,Zheng X.Increasing convex ordering of length queue in bulk queues[J].Operations Research Letters, 2008,36:123-126.

[7] Shaked M,Shanthikumar J G.Stochastic orders and their applications[M].New Xork:Academic Press,1994.

[8] Müller A.Some remarks on the supermodual order[J]. Journal of Multivariate Analysis,2000,73:107-119.

[9] Denuit M,Dhaene J,Goovaerts M,et al.Actuarial theory for dependence risks[M].New Xork:John Wiley,2005.

A Note on the Waiting Times for Bulk Arrival Queues with Dependent Variables

CAI Nan-lian
(School of Sciences,Jimei University,Xiamen 361021,China)

We consider single-server bulk arrivals queues G(X)/G/1 with the dependence between group sizes and inter-arrival times of customers and between service times and inter-arrival times,respectively.In these two cases,we show that stronger dependence between them leads to shorter waiting times in the increasing convex ordering sense.We also obtain bounds of waiting times in bulk arrival queues.

positive quadrant dependence;supermodular order;increasing convex order;Frëchet bound;bulk arrivals queues;waiting time

10.6043/j.issn.0438-0479.2015.02.015

O 211.5

A

0438-0479(2015)02-0238-04

2014-03-10 录用日期:2014-08-24

国家自然科学基金(11171278);集美大学黄慧贞学科建设基金

Email:cainanlan@163.com

蔡南莲.具有相依变量成批到达排队系统等待时间的注记[J].厦门大学学报:自然科学版,2015,54(2):238-241.

:Cai Nanlian.A note on the waiting times for bulk arrival queues with dependent variables[J].Journal of Xiamen University:Natural Science,2015,54(2):238-241.(in Chinese)