黄景廉，张椿玲

(西北民族大学电气工程学院，甘肃兰州730030)

旋转对称布尔函数的最高非线性度与最优代数免疫

黄景廉，张椿玲

(西北民族大学电气工程学院，甘肃兰州730030)

文章研究旋转对称布尔函数的最高扩散次数、最高非线性度和代数免疫性等问题.利用导数和e-导数证明了元数为偶数的完全2次齐次旋转对称布尔函数的非线性度达到布尔函数的最大非线性度.又利用导数从n次扩散性角度，证明了旋转对称Bent函数的存在性，即验证了最大非线性度旋转对称布尔函数的存在性.另外，利用导数证明了最优代数免疫旋转对称布尔函数的存在性，并给出了用Bent函数构造最优代数免疫旋转对称布尔函数的方法.利用导数还得出了一类旋转对称布尔函数的相关免疫性.

旋转对称布尔函数；Bent函数；导数；非线性度；相关免疫性；最优代数免疫

0 引言

代数免疫性、最优代数免疫、非线性度、最高非线性度、扩散性、高次扩散性、相关免疫性都是密码函数非常重要的安全性质.对这些性质的研究一直都在进行，特别是近年来提出的抵抗代数攻击的代数免疫性[1]，更是当前的研究热点[2～7].除此之外，其他密码学性质，如扩散性、相关免疫性和非线性度等，在构造布尔函数时也需要考虑.

Bent函数和旋转对称布尔函数都是密码学中的重要函数，是密码学界一直在认真研究的对象[8～14].旋转对称布尔函数中是否也含有Bent函数，如何用Bent函数构造出最优代数免疫旋转对称布尔函数等问题是需要研究的重要问题.如果以导数和e-导数作为研究工具，这些问题就较容易解决.本文将利用导数和e-导数来讨论旋转对称布尔函数的非线性度、扩散性、代数免疫性、旋转对称Bent函数的存在性和结构、最优代数免疫旋转对称布尔函数的存在性及构造等问题.

1 预备知识

布尔函数的导数是人们熟知的[15].需要给出布尔函数e-导数的概念.对e-导数与导数的关系及e-导数的性质，可参阅参考文献[16～18].

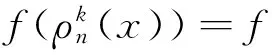
定义3[15]n元布尔函数f(x)=f(x1,x2,…，xn)∈GF(2)GF(2)n对r(1≤r≤n)个变元xi1,xi2,…，xir(1≤i≤n)的导数(偏导数)表示和定义为

∂f(x)/∂(xi1,xi2,…，xir)

(1)

当r=1时，式(1)即为f(x)=f(x1,x2,…，xn)对单个变元xi的导数，记为df(x)/dxi(i=1,2,…,n).经简单的计算化简，可得到如下便于使用的形式：

定义4[16～18]n元布尔函数f(x)=f(x1,x2,…，xn)∈GF(2)GF(2)n对r(1≤r≤n)个变元xi1,xi2,…，xir(1≤i≤n)的e-导数(e-偏导数)表示和定义为

ef(x)/e(xi1,xi2,…，xir)

(2)

当r=1时，式(2)即为f(x)=f(x1,x2,…，xn)对单个变元xi的e-导数，记为ef(x)/exi(i=1,2,…,n).经简单的计算化简，可得到如下便于使用的形式：

定义5 若f(x)∈GF(2)GF(2)n对所有α∈GF(2)n(1≤wt(α)≤k,k∈I+)，都有wt(f(x+α)+f(x))=2n-1，则称f(x)满足k次扩散准则，或f(x)是k次扩散函数.

Bent函数是密码学中重要的函数，也能用扩散准则来定义,即称函数f(x)∈GF(2)GF(2)n为Bent函数，当且仅当f(x)是n次扩散函数.

定义6 对任意满足1≤wt(ω)≤m的n元向量ω=(ω1,ω2，…，ωn)∈GF(2)n，函数f(x)=f(x1,x2,…，xn)∈GF(2)GF(2)n都有wt(f(x)+ωx)=2n-1(ωx=ω1x1+ω2x2+…+ωnxn)，则称f(x)为m阶相关免疫函数，m称为阶数.

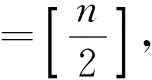
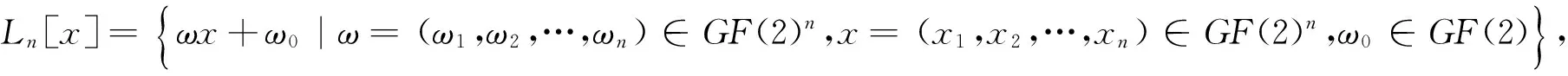
根据上述定义，可容易得到引理1～引理3.

引理1 布尔函数f(x)∈GF(2)GF(2)n是k次扩散函数的充分必要条件，对一切1≤r≤k，都有

wt(∂f(x)/∂(xi1,xi2,…，xir))=2n-1(i∈I+,r∈I+,1≤i1≤i2≤…≤ik≤k≤n).

引理2 对任意布尔函数f(x)∈GF(2)GF(2)n，有

f(x)=f(x)∂f(x)/∂(xi1,xi2,…，xir)+ef(x)/e(xi1,xi2,…，xir)

=f(x)df(x)/dxj+ef(x)/exj

(1≤i≤n,1≤r≤n,1≤i1≤i2≤…≤ir≤n,j∈I+)

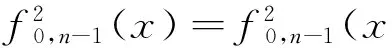
2 完全2次齐次旋转对称布尔函数与Bent函数、相关免疫函数

定理1先讨论完全2次齐次旋转对称布尔函数.

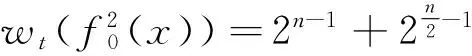
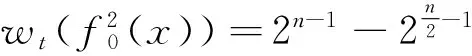
证明 由引理2，并经简单计算推导，有

所以有

所以有

证毕.

对n为偶数，1≤r≤n，当r为奇数时，有

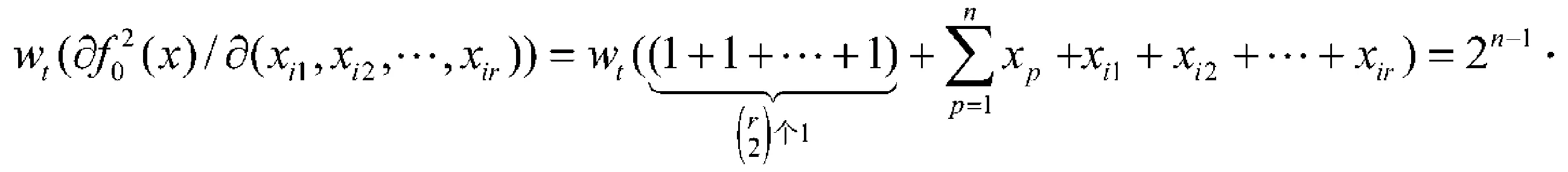
而当r为偶数时，有

推论2 偶数元完全2次齐次旋转对称布尔函数是n次扩散函数.

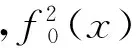
定理2 元数n≥5且n为奇数时，完全2次齐次旋转对称布尔函数是相关免疫函数.

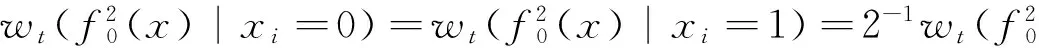
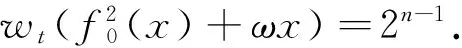
证毕.

3 旋转对称布尔函数与最优代数免疫函数

高非线性度是提高密码系统抵抗线性攻击能力的布尔函数的重要性质.定理3首先讨论利用2可分解为2个函数乘积的H布尔函数，构造出具有较高非线性度的相关免疫H布尔函数的问题.

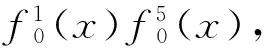
证毕.

推论3 两个完全齐次旋转对称布尔函数的乘积也必是完全齐次旋转对称布尔函数.

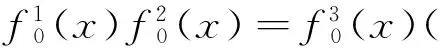
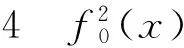
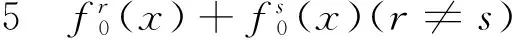
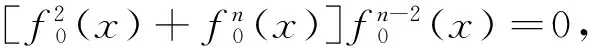
证毕.

(1)

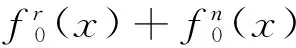
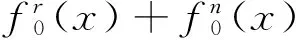
证毕.

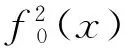
4 结语

[1] Courtois, N., and Meier, W. Algebraic attacks on stream ciphers with linear feedback[C]. Advances in Cryptology-EUROCRYPT 2003, Warsaw, Poland, 2003, LNCS, 2656:345-359.

[2] Carlet C and Zeng X Y. Further properties of several classes of Boolean functions with optimum algebraic immunity[J].Designs, Codes and Cryptography, 2009, 52(3): 303-338.

[3] Carlet C. A method of construction of balanced functions with optimum algebraic immunity[C]. Proceedings of the First International Workshop on Coding and Cryptography, Fujian, 2007，25-43.

[4] Li Y, Yang M, and Kan H B. Constructing and counting Boolean functions on even variables with maximum algebraic immunity[J]. IEICE Transactions on Fundamentals, 2010, 93-A(3): 640-643.

[5] Rizomiliotis P. On the resistance of Boolean functions against algebraic attacks using univariate polynomial representation[J]. IEEE Transactions on Information Theory, 2010, 56(8):4014-4024.

[6] Tu Z R and Deng Y P. A class of 1-resilient function with high nonlinearity and algebraic immunity[R]. Ryptography ePrint Archive, Report，2010, 2010/179.

[7] Wang Q, Peng J, Kan H, et al.. Constructions of cryptographically significant Boolean functions using primitive polynomials[J]. IEEE Transactions on Information Theory, 2010, 56(6): 3048-3053.

[8] 李春雷，张焕国，曾祥勇等. 一类Bent函数的二阶非线性度下界[J]. 计算机学报, 2012, 35(8):1588-1593.

[9] Sarkar S, Gangopadhyay S. On the second order nonlinearity of a cubic Maiorana-McFarland Bent Functions[J]. International Journal of Foundations of Computer Science, 2010, 21(3):243-254.

[10] Su S H, Tang X H. Construction of rotation symmetric Boolean functions with optimal algebraic immunity and high nonlinearity[J]. Designs, Codes and Cryptography, 2014, 71(2): 183-199.

[11] 陈银冬, 张亚楠, 田威. 具有最优代数免疫度的偶数元旋转对称布尔函数的构造[J]. 密码学报,2014, 1(5): 437-448.

[12] Sarkar S, Maitra S. Construction of rotation symmetric Boolean functions with optimal algebraic immunity[J]. Computation Systems, 2009, 12(3): 267-284.

[13] Fu S, Qu L, Li C, et al. Balanced rotation symmetric Boolean functions with maximum algebraic immunity[J]. IET Information Security, 2011, 5(2): 93-99.

[14] 董德帅, 李超, 屈龙江等. 偶变元MAI 旋转对称布尔函数[J]. 国防科技大学学报, 2012, 34(4): 85-89.

[15] 温巧燕,钮心忻,杨义先. 现代密码学中的布尔函数[M].北京:科学出版社,2000.

[16] Li, W., Wang, Z., Huang, J..The e-derivative of boolean functions and its application in the fault detection and cryptographic system[J]. Kybernetes, 2011, 40(5-6):905-911.

[17] 黄景廉,王卓. H布尔函数的相关免疫性与重量的关系[J]. 通信学报, 2012, 33(2):110-118.

[18] 赵美玲. 基于布尔e导数的特殊逻辑函数检测方法[J]. 浙江大学学报(理学版), 2014, 41(4):424-426.

The Hghest Nonlinearity and Optimal Algebraic Immunity of Rotation Symmetric Boolean Functions

HUANG Jing-lian，ZHANG Chun-ling

(College of Electrical Engineering, Northwest University for Nationalities, Lanzhou 730030, China)

The problems of RSBFs including the highest degree of propagation, the highest nonlinearity and algebraic immunity were studied in this article. Using the derivative and the e-derivative of the Boolean functions, the nonlinearity of quadratic homogeneous RSBFs was proved with even variables reaches the highest one of Boolean functions. Additionally, the existence of rotation symmetric Bent functions was verified using the derivative from n-degree propagation. That indicated that the existence of RSBFs with the highest nonlinearity had been proved. Moreover the paper proved that the existence of RSBFs with the optimal algebraic immunity, and provided the method of constructing RSBFs with the optimal algebraic immunity using Bent functions. The correlation immunity of a class of RSBFs using the derivative was also obtained.

RSBFs; Bent function; Derivative; Nonlinearity; Ccorrelation immunity; Optimal algebraic immunity

2015-05-20

黄景廉(1968—)，女，四川南充人，教授，主要从事计算机网络通讯安全方面的研究.

O231；TP309

A

1009-2102(2015)02-0001-07