基于Caputo分数阶导数的含时滞的非保守系统动力学的Noether对称性*
2015-06-08金世欣
金世欣,张 毅
(1.南京理工大学理学院,江苏 南京 210094;2.苏州科技学院土木工程学院,江苏 苏州 215011)
基于Caputo分数阶导数的含时滞的非保守系统动力学的Noether对称性*
金世欣1,张 毅2
(1.南京理工大学理学院,江苏 南京 210094;2.苏州科技学院土木工程学院,江苏 苏州 215011)
提出并研究基于Caputo分数阶导数的含时滞的力学系统的Noether对称性与守恒量。建立了含时滞的非保守系统的分数阶运动微分方程;根据系统的含时滞的分数阶Hamilton作用量在无限小群变换下的泛函不变性,给出了含时滞的分数阶Noether对称变换,Noether准对称变换以及Noether广义准对称变换的定义判据;研究了含时滞的分数阶Noether对称性与守恒量之间的联系,并举例说明结果的应用。
非保守系统;时滞;Caputo分数阶导数;Noether对称性;守恒量

近年来,Baleanu等[17-19]研究了分数阶模型下的含时滞的变分和最优化控制问题。2012年,Frederico和Torres[20]首次讨论了含时滞的变分和最优化控制问题的Noether定理;随后,张毅等[21-25]研究建立了含时滞的约束力学系统的Noether对称性与守恒量理论。尽管含时滞的分数阶变分和最优控制问题的研究已经取得了一些重要成果,但是研究状态变量或控制变量具有时滞的分数阶变分和控制系统的对称性与守恒量问题还是一个开放的课题,特别是在不同的分数阶模型下的对称性与守恒量的问题。本文将进一步研究基于Caputo分数阶导数定义下的含时滞的非保守系统动力学的Noether对称性与守恒量。建立相应力学系统的分数阶Noether对称性的定义和判据,并导出含时滞的分数阶Noether定理。
1 分数阶导数的定义及其若干性质
在这一部分我们简单地回忆一下将要用到的一些Riemann-Lionville以及Caputo分数阶导数的定义和性质。详细的讨论和证明,可参考文献[1-3]。
左Riemann-Lionville分数阶导数的定义如下
(1)
右Remiann-Lionville分数阶导数的定义如下
(2)
相应的Caputo分数阶导数的定义如下:左Caputo分数阶导数
(3)
右Caputo分数阶导数
(4)
其中Γ(*)为Gamma函数,满足k-1≤α (5) (6) 以及 (7) (8) (9) 假设力学系统由n个广义坐标qs(s=1,2,…,n)来确定。考虑非保守力学系统的Hamilton原理 (10) 其中,Lagrange函数以及非势广义力为 (11) (12) 且时滞常量τ (13) (14) 其中Ωs(t)为[t1-τ,t1]上的已知分段光滑函数。则原理(10)可写为 (15) 将式(15)的第三项,第五项进行变量替换t=θ+τ,并考虑初始条件(13),得到 (16) 考虑分部积分公式(6)和(7)以及(8)和(9),并考虑条件(13)和(14),则有 (17) 且有 (18) 以及 (19) 当满足条件 (20) 将(17),(18)以及(19)式代入(16)式,并考虑到积分区间的任意性以及δqs的独立性,得到 (21) 满足式(20),则方程(21)可称为Caputo导数下的含时滞的非保守系统的分数阶运动微分方程。如果广义非势力Q″s=0,则方程(21)就成为 (22) 满足式(20),则方程(22)为Caputo导数下的含时滞的分数阶Euler-Lagrange方程。 含时滞的分数阶Hamilton作用量为 (23) 引入r参数的有限变换群的无限小变换 (24) 其展开式为 (25) (26) (27) (28) 对(28)式的第五项,第六项进行变量替换t=θ+τ,并考虑边界条件(13),得到 (29) 注意到关系式 (30) 并考虑到分部积分公式(8)和(9)以及(6)和(7),则(29)式可变为 (31) 满足条件(20)。其中 (32) 式(29)和(31)是Caputo导数下的含时滞的分数阶Hamilton作用量变分的两个基本公式。 首先,给出Caputo导数下的含时滞的分数阶Noether对称变换的定义和判据。 定义1 如果含时滞的分数阶Hamilton作用量(23),在无限小群变换(24)作用下,满足条件 (33) 则称无限小变换为含时滞的分数阶Noether对称变换。 由定义1和公式(29)和(31),可得判据: 判据1 对于无限小变换(24),当t1≤t≤t2-τ时,满足条件 (34) 当t2-τ (35) 则变换(24)是含时滞的力学系统的分数阶Noether对称变换. 式(34)和(35)可表为:当t1≤t≤t2-τ时,有 (36) 当t2-τ (37) 当r=1时,式(36)和(37)称为含时滞的力学系统的分数阶Noether等式。 其次,研究Caputo导数下的含时滞的力学系统的分数阶Noether准对称性。 设L1是某个另外的Lagrange函数,如果变换(24)精确到一阶小量满足如下关系 (38) 那么称这种不变性为含时滞的分数阶Hamilton作用量(23)在无限小变换(24)下的准不变性。由此确定的L1与L具有相同的运动微分方程,因而变换(24)可称为含时滞的力学系统的分数阶准对称变换。于是有 定义2 如果含时滞的分数阶Hamilton作用量(23),在无限小群变换(24)作用下,满足条件 (39) 由定义2和公式(29)和(31),可得判据: 判据2 对于无限小变换(24),当t1≤t≤t2-τ时,满足条件 (40) 当t2-τ (41) 则变换(24)是含时滞的力学系统的分数阶Noether准对称变换. 式(40)和(41)可表为:当t1≤t≤t2-τ时, (42) 当t2-τ (43) 其中ΔG=εσGσ。当r=1时,式(42)和(43)称为含时滞的力学系统的分数阶Noether等式。 最后,讨论Caputo导数下的含时滞的非保守系统的分数阶广义Noether准对称性。 假设Caputo导数下的含时滞的非保守力学系统受到广义非势力Q″s的作用,如果精确到一阶小量满足如下条件 (44) 则相应不变性称为含时滞的分数阶Hamilton作用量(23)在无限小变换(24)下的广义准不变性,而变换(24)称为力学系统的含时滞的分数阶广义准对称变换。于是有 定义3 如果含时滞的分数阶Hamilton作用量(23),在无限小群变换(24)作用下,满足条件 (45) 则称无限小变换为含时滞的力学系统的分数阶Noether广义准对称变换。 由定义3和公式(29)和(31),可得判据: 判据3 对于无限小变换(24),当t1≤t≤t2-τ时,满足条件 (46) 当t2-τ (47) 则变换(24)是含时滞的力学系统的分数阶广义Noether准对称变换。 式(46)和(47)可表为:当t1≤t≤t2-τ时, (48) 当t2-τ (49) 当r=1时,式(48)和(49)称为含时滞的力学系统的分数阶Noether等式。 利用判据1-判据3或含时滞的分数阶Noether等式(36)和(37),(42)和(43),(48)和(49)可以判断含时滞的力学系统的分数阶Noether对称性。 本节我们研究Caputo导数下的含时滞的力学系统的分数阶守恒量。首先给出所论含时滞的力学系统的分数阶守恒量的定义。 (50) 对于含时滞的Lagrange系统(22),如果能找到系统的分数阶Noether对称变换或分数阶Noether准对称变换,便可求得相应的分数阶守恒量。于是,有如下定理。 定理1 对于含时滞的Lagrange系统(22),如果无限小变换(24)是定义1下的分数阶Noether对称变换,则系统存在r个线性独立的分数阶守恒量,当t1≤t≤t2-τ时,形如 (51) 当t2-τ (52) 证明 由于无限小变换(24)是系统的分数阶Noether对称变换,由定义1,以及式(31),并将方程(31)代入式(33),由积分区间的任意性和εσ的独立性,并利用含时滞的Lagrange方程(22),得到,当t1≤t≤t2-τ时,有 (53) 当t2-τ (54) 对(53)和(54)式进行积分,便得到结果。 定理2 对于含时滞的Lagrange系统(22),如果无限小变换(24)是定义2下的分数阶Noether准对称变换,则系统存在r个线性独立的分数阶守恒量,当t1≤t≤t2-τ时,形如 Gσ=const. (55) 当t2-τ (56) 证明 由于无限小变换(22)是系统的Noether准对称变换,由定义2,以及式(39),并将方程(31)代入式(39),由积分区间的任意性和εσ的独立性,并利用含时滞的Lagrange方程(22),易知定理成立。证毕。 下面,我们进一步讨论含时滞的非保守力学系统的分数阶Noether定理。 定理3 对于含时滞的非保守系统(21),如果无限小变换(24)是定义3下的分数阶广义Noether准对称变换,则系统存在r个线性独立的分数阶守恒量(53)和(54)。 证明 由于无限小变换(24)是系统的Noether广义准对称变换,由定义3,以及(45)式,并将方程(31)代入式(45),由积分区间的任意性和εσ的独立性,并利用含时滞的Lagrange方程(21),易知定理成立。 定理1-3称为含时滞的非保守力学系统的分数阶Noether定理。由Noether定理可知,对于所论分数阶模型下的含时滞的非保守系统,如果能找到系统的一个含时滞的分数阶Noether对称变换,便有可能得到系统的一个分数阶守恒量。 例 已知力学系统的Lagrange函数和非势广义力为 (57) 其中质量m及阻尼系数c均为常数。且t∈[t1,t2],时滞常量τ 系统的运动微分方程给出 (58) 由含时滞的分数阶Noether等式(48)和(49)给出 (59) 方程(59)有解 (60) (61) 生成元(60)和(61)都相应于系统的Noether广义准对称变换.由定理3,得到 I1=0 (62) (63) 因此,生成元(62)相应的分数阶守恒量是平庸的.若分数阶导数不存在时,方程(63)就成为含时滞的运动微分方程 (64) 式(63)就成为 (65) 式(65)是含时滞的非保守系统的广义Noether准对称性相应的守恒量。若时滞常量τ=0时,式(65)就成为经典力学系统的相应的守恒量 (66) 提出并研究了Caputo导数下含时滞的非保守动力学系统的分数阶Noether对称性与守恒量。建立了含时滞的分数阶Hamilton原理(15)和(16),并由此进一步导出了含时滞的分数阶Lagrange方程(21)。给出了含时滞的分数阶Hamilton作用量变分的两个基本公式,建立了含时滞的分数阶Noether对称性的定义和判据,并得到了相应的分数阶Noether定理。文章的方法和结果具有普遍性,可进一步应用于Caputo导数下含时滞的分数阶非完整力学系统,分数阶Hamilton系统以及分数阶Birkhoff系统等。 [1] OLDHAM K B, SPANIER J. The fractional calculus[M]. San Diego: Academic Press, 1974. [2] SAMKO S G, KILBAS A A, MARICHER O I. Fractional integrals and derivatives: theory and applications[M]. Breach, 1993. [3] PODLUBNY I. Fractional differential equations[M]. San Diego: Academic Press,1999. [4] RIEWE F. Nonconservation lagrangian and Hamiltonian mechanics[J]. Phys Rev E, 1996,53(2):1890-1899. [5] RIEWE F. Mechanics with fractional derivatives[J]. Phys Rev E, 1997,55(3): 3581-3592. [6] AGRAWALl O P. Formulation of Euler-Lagrange equations for fractional variational problems [J]. J Math Anal Appl, 2002, 272(1): 368-379. [7] AGRAWALl O P. Fractional variational calculus in terms of Riesz fractional derivatives[J]. J Phys A: Math Theor, 2007, 40(24): 6283-6303. [8] FREDERICO G S F, TORRES D F M. Fractional conservation laws in optimal control theory[J]. Nonlinear Dyn, 2008, 53(3):215-222. [9] FREDERICO G S F, TORRES D F M. Fractional optimal control in the sense of caputo and the fractional Noether’s theorem[J]. Int Math Forum, 2008, 3 (10): 479 - 493.. [11] ZHANG Y, ZHAI X H. Noether symmetries and conserved quantities for fractional Birkhoffian systems[J]. Nonlinear Dyn, 2015, 81(1/2):469-480. [12] BALEANU D. Fractional Hamilton formalism within Caputo’s derivative[J]. Czech J Phys, 2006, 56 (10/11); 1087-1092. [13] MALINOWSKA A B, TORRES D F M. Fractional variational calculus in terms of a combined Caputo derivative[J]. Fract Calcu Appl Anal, 2011, 14(4): 523-537. [14] 张毅. 相空间中类分数阶变分问题的Noether对称性与守恒量[J]. 中山大学学报:自然科学版, 2013, 52(4): 45-50. [15] 龙梓轩,张毅.基于正弦周期律拓展的分数阶积分的变分问题的Noether定理[J].中山大学学报:自然科学版, 2013, 52(5): 51-56. [16] 何胜鑫,朱建清.基于分数阶模型的相空间中非保守力学系统的Noether准对称性[J].中山大学学报:自然科学版, 2015, 54(4): 5-11. [17] BALEANU D, MARAABA T, JARAD F. Fractional variational principles with delay[J]. J Phys A:Math Theor, 2008, 41(31): 315403(1-8). [18] JARAD F, ABDELJAWAD T, BALEANU D. Fractional variational principles with delay within Caputo derivatives[J]. Math Phys , 2010, 1(65): 17-28. [19] JARAD F, ABDELJAWAD T, BALEANU D. Fractional variational optimal control problems with delayed argument[J]. Nonlinear Dyn, 2010, 62(3): 609-614. [20] FREDERICO G S F, TORRES D F M. Noether’s symmetry theorem for variational and optimal control problem with time delay[J]. Num Algebra, Contr Optim, 2012, 2(3): 619-630. [21] 张毅,金世欣.含时滞的非保守系统动力学的Noether对称性[J].物理学报,2013, 62(23): 214502. [22] JIN S X, ZHANG Y. Noether symmetry and conserved quantity for a Hamilton system with time delay[J]. Chin Phys B, 2014, 23(5): 054501. [23] 金世欣,张毅.相空间中含时滞的非保守力学系统的Noether定理[J].中山大学学报:自然科学版, 2014, 53(4): 18-23. [24] ZHAI X H, ZHANG Y. Noether symmetries and conserved quantities for Birkhoffian systems with time delay[J]. Nonlinear Dyn, 2014, 77(1/2): 73-86. [25] JIN S X, ZHANG Y. Noether theorem for non-conservative Lagrange systems with time delay based on fractional model[J]. Nonlinear Dyn, 2015, 79(2): 1169-1183. Noether Symmetries for Non-Conservative Lagrange Systems with Time Delay Based on Caputo Fractional Derivative JINShixin1,ZHANGYi2 (1.College of Physics, Nanjing University of Science and Technology, Nanjing 210094, China;2.College of Civil Engineering, Suzhou University of Science and Technology, Suzhou 215011, China) The Noether symmetries and the conserved quantities of a mechanical system with time delay based on Caputo fractional derivatives are proposed and studied. Firstly, the fractional Lagrange equations with time delay are established. Secondly, based upon the invariance of the fractional Hamilton action with time delay under the group of infinitesimal transformations, the fractional Noether symmetric transformations, the definitions and criteria of the Noether quasi-symmetric transformations and generalized Noether quasi-symmetric transformations with time delay are given. Finally, the relationship between the fractional symmetries and the fractional conserved quantities with time delay are studied. At the end, an example is given to illustrate the application of the results. nonconservative system; time delay; Caputo fractional derivative; Noether symmetry; conserved quantity 10.13471/j.cnki.acta.snus.2015.05.011 2015-02-03 国家自然科学基金资助项目(10972151,11272227) 金世欣(1987年生),男;研究方向:一般力学与力学基础;通讯作者:张毅;E-mail:weidiezh@gmail.com O316 A 0529-6579(2015)05-0049-08
2 含时滞的分数阶运动微分方程
3 含时滞的分数阶Hamilton作用量变分



4 含时滞的分数阶Noether对称性

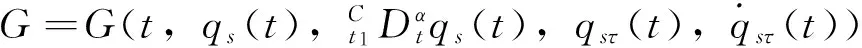
5 含时滞的分数阶Noether定理

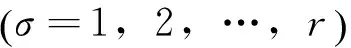
6 算 例



7 结 论

