Zhang Chuang Zhao Honglin Jia Min

(Communication Research Center, Harbin Institute of Technology, Harbin 150080, China)



An improving energy efficiency cooperation algorithm based on Nash bargaining solution in selfish user cooperative networks

Zhang Chuang Zhao Honglin Jia Min

(Communication Research Center, Harbin Institute of Technology, Harbin 150080, China)

A bandwidth-exchange cooperation algorithm based on the Nash bargaining solution (NBS) is proposed to encourage the selfish users to participate with more cooperation so as to improve the users’ energy efficiency. As a result, two key problems, i.e., when to cooperate and how to cooperate, are solved. For the first problem, a proposed cooperation condition that can decide when to cooperate and guarantee users’ energy efficiency achieved through cooperation is not lower than that achieved without cooperation. For the second problem, the cooperation bandwidth allocations (CBAs) based on the NBS solve the problem how to cooperate when cooperation takes place. Simulation results show that, as the modulation order of quadrature amplitude modulation (QAM) increases, the cooperation between both users only occurs with a large signal-to-noise ratio (SNR). Meanwhile, the energy efficiency decreases as the modulation order increases. Despite all this, the proposed algorithm can obviously improve the energy efficiency measured in bits-per-Joule compared with non-cooperation.

cooperation algorithm; Nash bargaining solution (NBS); resource-exchange; quadrature amplitude modulation (QAM)

The cooperation diversity[1]takes advantage of the broadcasting of wireless networks, so the relay node can forward the replica of the source node’s data. Moreover, it can enlarge system coverage and increase link reliability, and it will be a key technology in further wireless networks. Generally, it is true to assume that the communicating users voluntarily cooperate during scenarios of relief and military applications. However, this assumption is not realistic when the users serve different tasks or belong to different authorities[2-3], since the cooperative action will cause the consumption of users’ resource (e.g., power and bandwidth). Ultimately, a selfish user will not participate in cooperation to save his/her own resource, and that will dramatically degrade the performance of the whole network. Therefore, how to encourage the selfish user to participate in cooperation is an urgent issue.

The main methods for stimulating the selfish users to cooperate can be classified into three categories: the reputation-based mechanism[4-5], the pricing-based mechanism[6-7]and the resource-exchange mechanism[8-11]. The first two mechanisms always rely on the use of tamper-proof hardware. However, the resource-exchange mechanism can avoid the application of tamper-proof hardware. We study the resource-exchange mechanism in this paper. In Ref.[8], the authors proposed a cooperation strategy based on the Nash bargaining solution (NBS) in cooperative relay networks. They modeled the problem of sharing bandwidth between two users as a two-person bargain. A game-theoretic approach for power allocations in bidirectional cooperation communication was proposed in Ref.[9], where two nodes send data to the destination as source and each source node has to relay the other’s data. In their work, the problem how much power each node contributes to relaying other nodes’ data is solved by using the Stackelberg game. According to the scenario of a primary user and multiple secondary users in cognitive radio networks, the length of channel access time that primary users leave for selected secondary users and the amount of power that secondary users contributed to help primary users’ transmission are tackled in Ref.[10]. Zhang et al.[11]proposed a cooperation strategy based on sharing a time slot resource aiming at a model of multiple users. Also, a fast particle swarm optimization algorithm was put forward to obtain the Nash equilibrium solution. The thesis of energy efficiency was also studied in Refs.[12-13], but the fundamental difference between their works and ours is the measure of energy efficiency. In Refs.[12-13], residual energy among all nodes was used to measure the energy efficiency; however, we use the amount of bits which are transmitted by the unit of energy (bit/J) to measure the energy efficiency. In Ref.[12], the authors proposed a distributed algorithm based on the regret matching procedure to obtain the correlated equilibrium which decides whether the nodes are to cooperate or not. The proposed algorithm may break down when the users exist only one or two times in the networks. In Ref.[13], the coalition game is used to decide the numbers of cooperative nodes, and the proposed algorithm is based on the premise that the cooperative nodes have the same benefit or belong to the same authority. This premise is not the same as ours, since the nodes merely focus on their own interest in no dedicated relay station networks (RSs) which also can be named user cooperation networks.

Cooperation bandwidth allocations (CBAs) between users are studied in Ref.[8], but the Nash equilibrium of CBAs is obtained by geometrical interpretation without analytical solution. Meanwhile, the authors did not consider the effect of different modulations on the cooperation strategy[8]. Our main contributions can be summarized as follows: 1) A cooperation algorithm based on the NBS is proposed; therefore, the critical problems that when to cooperate and how to cooperate are solved for selfish user cooperative networks. Consequently, both users can improve their energy efficiency by adopting the proposed cooperation algorithm. 2) We revisit the CBAs of NBS between cooperation users, and the analytical solution is obtained through the Lagrange multiplier method instead of geometrical interpretation as used in Ref.[8]. 3) The influence on the cooperation algorithm is researched when different modulation orders of QAM are used.

1 System Model

In this paper, we consider a symmetric relay scenario composed of two users and an access point (AP), in which a user acts as source as well as a potential relay node. The network is assumed to be geographically static or quasi-static so that the time scale of the algorithm convergence is shorter than the channel variations, and it works on frequency division multiple access (FDMA); hence, there is no interference between user 1 and user 2. The antennas are omnidirectional, and each user is allocatedWbandwidth for transmission.

The illustration of CBAs is given in Fig.1, where user 1 usesW12(W12∈[0,W]) to relay user 2’s information, and user 2 usesW21(W21∈[0,W]) to relay user 1’s information. It means that user 1 can transmit his/her own information only using the remaining (W-W12) of his/her bandwidth and onlyW21will be relayed by user 2.

Fig.1 Illustration of CBAs (unit: Hz)

The information carried onW21can be transmitted in a cooperative manner, and he/she can obtain the cooperative diversity. Also, the information carried on (W-W12-W21) will be transmitted to the AP without any cooperative diversity. Similarly, user 2’s information carried onW12can obtain cooperative diversity, and the remaining (W-W12-W21) will be transmitted to the AP without it. Since the relay node cannot relay the information greater than that originating from the source node, we have constraints thatW21≤W-W12andW12≤W-W21. Then, we can haveW12+W21≤W. The constraints can be expressed as

W12≥0,W21≥0,W12+W21≤W

(1)

Both users need to help each other in relaying, so the amount of bandwidth that a user is willing to take out to exchange for the other user’s cooperation is a problem. We define the problem of bandwidth sharing between two selfish users as CBAs.

2 User Satisfaction Metric

Generally, a selfish user in a wireless network is interested in two factors: throughput and energy consumption. This means that he/she wants to achieve as much throughput as possible while consuming less energy. Therefore, there is a tradeoff between throughput and energy consumption, which can quantify a user’s satisfaction in transmitting its own information[14]. Saraydar et al.[15]proposed a function that involves these two factors, and we quote their definition:

(2)

which can be explained as the average amount of data received correctly per unit of energy consumed. In Eq.(2),piis the transmit power, andTi(pi) is the user’s efficient throughput, which is expressed as

(3)

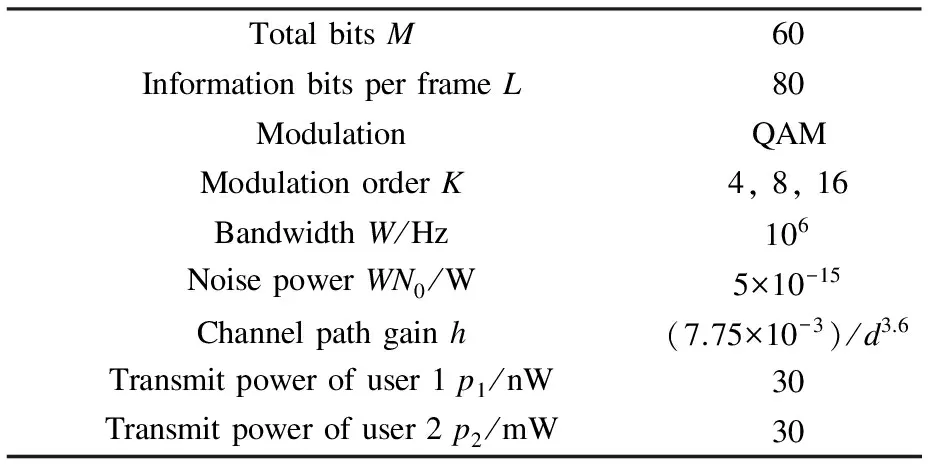
whereL

f(γi)=(1-2BER(γi))M

(4)

and it is used for approximating the frame success rate (FSR).γiis as follows:

(5)

whereN0Wandhare the noise power and channel path gain, respectively. Here,h=(7.75×10-3)/d3.6anddis the distance between the receiver and transmitter.

When the QAM modulation is adopted, BER(·) can be expressed as

(6)

whereKis the modulation order,γbis the signal to noise ratio per bit, andQ(·) is the standard error function, which can be expressed as

(7)

The relationship betweenγbandγiis

(8)

3 User Utility Function

In general, a game is composed of participants, the non-empty strategies set of each participants and the utility function defined on the set of strategies. In this paper, the participants are user 1 and user 2, and the strategies set are cooperation bandwidthW12(W12∈[0,W]) andW21(W21∈[0,W]). Following the definition in Eq.(2), if the transmit power of user 1 isp1, the utility function of user 1 can be expressed as

(9)

(10)

(11)

(12)

whereγ1a,γ12, andγ2aare the SNRs of the wireless channels from user 1 to AP, from user 1 to user 2, and from user 2 to AP, respectively. Substituting Eqs.(10) and (11) into Eq.(9), we can obtain the utility function of user 1 as

(13)

Similarly, the utility function of user 2 can be expressed as

(14)

(15)

whereγ21is the received SNR of the wireless channel from user 2 to user 1.

4 CBAs based on NBS

LetSirepresent the set of feasible payoff allocations for useri(i=1,2), we have

(16)

Then, the set of feasible payoff allocations that the two users can obtain when they work together is

S={U=(U1,U2)|U1∈S1,U2∈S2}

(17)

Bythesimplederivation,wecanobtain

(18)

α≥0,β≥0,α+β≤1

(19)

(20)

which is well known as the NBS. Then the CBAs can be modeled as the Nash bargaining problem that was proved in Ref.[8]. Hence, the NBS function of CBAs can be expressed as

(21)

(22)

(23)

Substituting Eqs.(13), (14), (22) and (23) into Eq.(21), we can obtain the NBS function of CBAs, which also can be named as the cooperation gain product (CGP), and then we have

s.t.W12≥0,W21≥0,W12+W21≤W

(24)

Combining Eqs.(1) and (24), we use the Lagrange multiplier method to determineW12andW21, and we obtain

(25)

Taking the derivations of variablesW12,W21, andλ, and, furthermore, making derivations be zeros, we can obtain the CBAs as

(26)

To guarantee that the utility of cooperation is not lower than non-cooperation, we have the following constraints:

(27)

By solving above inequalities, we have the cooperation condition:

(28)

If the CBAs satisfy the above constraints, the cooperation between user 1 and user 2 can be reached, or there is no cooperation between them. Under the non-cooperation case, the CBAs are

(29)

Based on above analysis, we proposed a bandwidth-exchange cooperation algorithm using NBS to stimulate the selfish users to participate in cooperation. The proposed algorithm is as follows:

Algorithm 1 Bandwidth-exchange cooperation algorithm based on NBS

2) User 1 and user 2 judge cooperation condition:

3) If both users select cooperation, then CBAs are executed according to Eq.(26).

4) If not, there is no cooperation between user 1 and user 2.

5 Simulation Results and Analysis

The adopted model is similar to Ref.[8], and where the AP is located at the origin and the two users are on theXaxis. The coordinates of user 1 and user 2 are (d1, 0) and (d2, 0), respectively. We assume that both users adopt the same modulation order simultaneously. The simulation parameters are shown in Tab.1.

Fig.2 shows the CGP of user 1 and user 2 adopting different order QAM vs. differentγ2awhen the distance between user 1 and AP is 700 m. Also, the CGP is measured in (bit/J)2. When the CGP is greater than zero, both users can benefit from cooperation, which means that the cooperation between both users is reached. Hence,

Tab.1 Simulation parameters

the CGP of user 1 and user 2 decides when to cooperate. Moreover, we define the range of SNR where cooperation occurs as the cooperation range. In Fig.2, we can observe that the SNR becomes larger, which creates the cooperation between two users reached, as the modulation order becomes higher. Also, the amplitude of the cooperation gain product decreases when the modulation order increases.

Fig.2 The CGP of user 1 and user 2 vs. different γ2a

Fig.3 illustrates the CBAs of both users adopting different modulation orders, and the simulation parameters are the same as those in Fig.2. In Fig.3, the solid line represents the bandwidth that is used by user 1 to relay user 2’s information, while the dotted line represents the bandwidth that is used by user 2 to relay user 1’s information. The intersection of the two lines means that both users have the same channel state. When the SNR is lower than the value of intersection, user 2 is the willing to contribute more bandwidth for cooperation to exchange user 1’s help, since the user 1’s channel state is better than user 2’s within this range. When the SNR is greater than the value of the intersection, the situation is the opposite. Also, the CBAs are zeros outside the cooperation range which means that there is no cooperation between either users. From Fig.3, we also can see that the cooperation range becomes smaller as the modulation order increases. Furthermore, cooperation between both users only occurs under the condition of a large SNR.

In Fig.4, the solid line represents the efficient energy efficiency sum (EEES) of both users adopting the proposed algorithm, and the dotted line represents the efficient energy efficiency sum of both users with no cooper-ation. From Fig.4, we can observe that the EEES increases as the modulation decreases. In general, compared to no cooperation, the proposed algorithm can improve energy efficiency.

(a)

(b)

(c)

6 Conclusion

To stimulate the selfish user to cooperate, a resource-exchange algorithm based on NBS is proposed according to the model where a user acts as the source mode and the potential relay node. Then the problems that the amount of bandwidth contributes to relaying other users’ infor-mation and the amount of bandwidth used to transmit its own information are solved. Furthermore, the influence on the cooperation algorithm is investigated when users adopt different modulation orders of QAM under different SNRs. The cooperation range becomes nearer to AP and smaller as the modulation order increases, and the cooperation only occurs at large SNRs when high modulation is used. Meanwhile, energy efficiency is clearly improved as the modulation order decreases. In conclusion, compared to non-cooperation, the proposed algorithm can increase the energy efficiency that is measured in bit-per-Joule.

(a)

(b)

(c)

[1]Laneman J N, Tse D N C, Wornell G W. Cooperative diversity in wireless networks: efficient protocols and outage behavior [J].IEEETransactionsonInformationTheory, 2004, 50(12):3062-3080.

[2]Jaramillo J J, Srikant R D. Distributed and adaptive reputation mechanism for wireless ad-hoc networks [C]//ProcACMMobicom. Montreal, Canada, 2007: 87-97.

[3]Xe K, Shen M, Ye M J. A model approach to estimate peer-to-peer traffic matrices[C]//ProcIEEEINFOCOM. Shanghai, China, 2011: 676-684.

[4]Yu W, Liu K J R. Secure cooperation in autonomous mobile ad-hoc networks under noise and imperfect monitoring: a game-theoretic approach [J].IEEETransactionsonInformationForensicsandSecurity, 2008, 3(2): 317-330.

[5]Al-Karaki J N, Kamal A E. Stimulating node cooperation in mobile ad-hoc networks [J].WirelessPersCommun, 2008, 44(2): 219-239.

[6]Cong L, Zhao L, Zhang H, et al. Pricing-based game for spectrum allocation in multi-relay cooperative transmission networks [J].IETCommunications, 2011, 5(4): 563-573.

[7]Lin P, Zhang J, Zhang Q, et al. Enabling the femtocells: a cooperation framework for mobile and fixed-line operators [J].IEEETransactionsonWirelessCommunications, 2013, 12(1): 158-167.

[8]Zhang Z Y, Shi J, Chen H-H, et al. A cooperation strategy based on nash bargaining solution in cooperative relay networks [J].IEEETransactionsonVehicularTechnology, 2008, 57(4): 2570-2577.

[9]Janzamin M, Pakravan M, Sedghi H. A game-theoretic approach for power allocation in bidirectional cooperative communication [C]//ProcIEEEWCNC. Sydney, Australia, 2010:1-6.

[10]Wang H, Gao L, Gan X, et al. Cooperative spectrum sharing in cognitive radio networks-a game-theoretic approach [C]//ProcIEEEICC. Cape Town, South Africa, 2010: 1-5.

[11]Zhang Guopeng, Yang Kun, Li peng, et al. Resource-exchange based cooperation stimulating mechanism for wireless ad hoc networks [C]//ProcIEEEICC. Ottawa, Canada, 2012: 297-305.

[12]Wu D, Cai Y M, Zhou L, et al. Cooperative strategies for energy-aware ad hoc Networks: a correlated equilibrium game-theoretic approach [J].IEEETransactionsonVehicularTechnology,2013, 62(5):2303-2314.

[13]Wu D, Cai Y M, Zhou L, et al. A cooperative communication scheme based on dynamic coalition formation game in clustered wireless sensor networks [J].IEEETransactionsonWirelessCommunications, 2012, 11(3): 1190-1200.

[14]Shastry N, Adve R S. Stimulating cooperative diversity in wireless ad hoc networks through pricing [C]//ProcIEEEICC. Istanbul, Turkey, 2006:3747-3752.

[15]Saraydar C U, Mandayam N B, Goodman D J. Pricing and power control in a multicell wireless data network [J].IEEEJournalonSelectedAreasinCommunications, 2001, 19(10): 1883-1892.

[16]Nash J. The bargaining problem [J].Econometrica, 1950, 28(2): 155-162.

自私用户协作网络中基于纳什谈判解的能量效率提升协作算法

张 闯 赵洪林 贾 敏

(哈尔滨工业大学通信技术研究所,哈尔滨150080)

为了促使自私用户合作并在合作中提高能量效率,提出了一种基于纳什谈判解的带宽交换协作算法．解决了用户协作网络中的2个关键问题:何时合作及如何合作．首先,针对何时合作问题,提出了用户合作条件以保证用户在合作时获得的能量效率不低于非合作时的能量效率;其次,针对如何合作问题,提出了基于纳什谈判解的协作带宽分配方法．仿真结果表明,随着QAM调制阶数的增加,用户只能在更大的信噪比下建立合作．同时,能量效率随着调制阶数的增加而降低．和非合作方式相比,所提算法能明显提升协作用户间的能量效率．

协作算法;纳什谈判解;带宽交换;QAM调制

TP393.01

Foundation items：The National Natural Science Foundation of China (No.61201143), Innovation Foundations of CAST (ITS) (No.F-W-YY-2013-016), the Fundamental Research Funds for the Central Universities (No.HIT.IBRSEM.201309).

：Zhang Chuang, Zhao Honglin, Jia Min．An improving energy efficiency cooperation algorithm based on Nash bargaining solution in selfish user cooperative networks[J]．Journal of Southeast University (English Edition),2015,31(2):181-187．

10.3969/j.issn.1003-7985.2015.02.004

10.3969/j.issn.1003-7985.2015.02.004

Received 2014-11-20．

Biographies：Zhang Chuang(1986—), male, graduate; Zhao Honglin (corresponding author), male, doctor, professor, hlzhao@hit.edu.cn.