☉江苏省海安县曲塘中学 徐成武

轻沙走马路无尘
——谈数学解题的三重境界

☉江苏省海安县曲塘中学 徐成武

高中数学解题教学的初级目的是为了提高学生应试的水平，提高其在高考中的应试分数，这是绝大部分学生在中学数学解题教学中比较切合实际的目标.另一方面，课程改革在稳步前行，课程改革的目标非常清晰：要致力于学生对形式化数学本质的理解，加强学生对数学应用的实践，逐步渗透数学思想方法于数学教学之中，不断培养学生在数学问题解决过程中的创新意识和思维导向的指导，既形成扎实的基本功，也形成一定的运用、创新能力.

陕西师大罗增儒教授在谈到如何解题时，曾经这样谈及：对教师而言，首先要会做题，这是起码的基本能力，其次是会变题，能通过一个问题变换到一类问题，进而解决是更高思维逻辑的体现，最后是用思想方法归类解题，这是最高境界的体现，当学会了从思想方法的高度来看如何解数学问题，那么中学数学解决问题的方法永远是那么几类.笔者思索罗教授在《解题学导论》中的一席话，将其落地生根、更接中学数学解题而言，应该恰好可以理解为中学数学解题教学的三种境界：其一，如何解一般问题，这里不外乎数学问题解决的基本手段（包括熟练化、系统化、反思等），笔者称之为一维数轴式的解题；其二，如何解一类问题，稍难的数学问题都可以深化、研究，将其归纳小结，通过一个问题可以引导学生解决一类问题，笔者称之为二维坐标式的解题；最后，针对一系列问题，总结其问题解决的思想方法，站在更高的位置来看待问题的解决，这是数学解题的更高境界，笔者称之为三维空间式的解题.将解题教学用三种螺旋式上升关系进行合理衔接，正是解题教学的三重境界.本文从案例结合的角度，探讨解题教学如何层层递进，让师生在不知不觉中感受数学解题的魅力.

境界一：一维数轴式解题

单一的解题，是指仅仅孤立地解决问题.在新知学习阶段，学生往往处于一维数轴式的处理模式.为何如此比喻呢？数学家王元说过：数学知识像分布在数轴上的数，比方说数字0犹如集合，随着认识的增加，我们认识了数字1，这就是集合之后的函数内容，只有一个个数字的学习、认知才能将数轴上的数字逐一认识，这里的过程正是单一模式的解决问题.笔者认为，教师解题教学的首要问题是如何学会一维数轴式解题，这需要学生三个方面的提升：首先是数学概念的认知和内化，用王元教授的话说即是基本保障；其次是典型问题的感知、感悟，这是将概念落到实处的体现；最后是一定的巩固训练，对于单一数轴式解题的提高和培养，不必要以题海训练模式进行低效反复操作从而使学生丧失学习积极性.因此，将上述环节有条不紊、循序渐进地展开，是做好解题教学第一重境界的基本.

案例1：判断△ABC解的个数（必修5第一章正弦定理习题）.

问题：在△ABC中，由下列各组条件求解三角形，其中有两个解的是_________________.

①b=20，A=45°，C=80°；②a=30，c=28，B=60°；

③a=14，b=16，A=45°；④a=12，c=15，A=120°；

利用正弦定理判断△ABC解的个数的可能性，从实际教学效果来看，学生掌握的程度离教师的期望是比较远的.笔者认为学生并没有认识到该知识的一维数轴式上的重点：（1）何种三角形才会有两解？（2）有多解的三角形如何判断？因此笔者认为，解决问题之前，先解决该知识的基本环节（如表1和表2）.

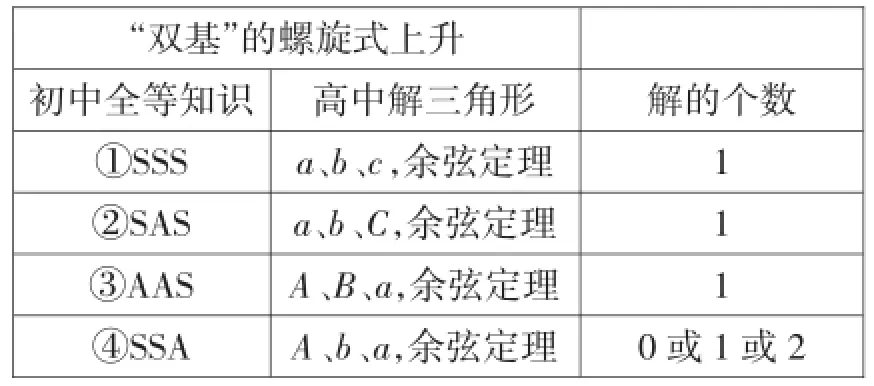
表1

表2

在学生掌握上述基础知识后，继续解决给出的相关问题.

分析：对于①，AAS，必定一解；

对于②，SAS，必定一解；

对于③，SSA，sinA＜1且a＜b，两解；

对于④，SSA，且C＞A=120°，无解；

对于⑤，SSS，必定一解；

对于⑥，SSA，sinB=1，一解.

说明：从本题的教学可以看出，笔者引导学生解决问题的步骤是按照学生认知的三个步骤进行的，既有数学概念、性质的回顾，也有对其问题解决过程的启发和引导，并在问题解决最后以同一知识类型问题给予巩固，这样的解决方式对于单一知识的问题解决是比较完备的，在一维数轴式上的知识点解决也是线性的、系统化的，让学生在解题第一重境界的领悟上做到扎实有序、循序渐进.

境界二：二维坐标式解题

如果说一维数轴式解题教学是横向的一种实施，那么教师完善解题教学的第二境界需要对解题教学进行纵向的尝试.一维数轴式解题是对单一知识的解决，但是单一知识存在着知识点运用的简单性、直接性，使得学生无法将复杂问题通过纯粹单一解题进行巩固训练提升，必须依赖对知识更深程度的分析，通过纵向的一种变化来加强.笔者认为这种方式加强的数学解题教学，是对知识间联系的一种整合，它有利于知识之间交叉混合解决问题，是对前一种境界的提升.华师大张奠宙教授专门就新课程下与时俱进的“双基”提出了独到的见解：传统的“双基”是指加强学生的基础知识和基本技能，但是这远远不够，而今数学教学还需要将这些基础知识进行合理整合的使用，我认为方式可以是一题多解加深知识间的衔接，或者是一题多变的探索，通过一个问题加深一类问题的解决，这种方式才是与时俱进的“双基”.笔者认为，二维坐标式的数学解题教学正是符合了这一精神的教学所在.

案例2：在△ABC中，M是BC的中点，AM=3，BC=10，则___________.

分析：学生思考后提出两种解法，一是根据问题结论的普适性，通过特例“正三角形”得出答案；二是利用平面向量基本定理将未知向量用已知向量进行分解的一般化处理方法.教师在对这两种方法做出评价，肯定了学生的思考后，提问有没有更好的方法.在学生思考不得其所时，给出“平行四边形两条对角线的平方和等于四条边的平方和”的证明过程，启发学生通过自主阅读，从该命题证明|a+b|2+|a-b|2的过程中来寻找启动问题的原型a·b的处理方式，由学生来推导得到最终将其应用于启动问题，起到了最大程度简化的作用，使学生初步认识到了该恒等式的价值所在.

变式1：在等腰直角三角形ABC中，AB=AC=2，D、E是线段BC上两点，且的取值范围是________.（在学生思维的最近发展区进行巩固，即学即用，使学生进一步看到“极化恒等式”的应用价值，从而引出学生继续深入学习的热情）

变式2：在半径为1的扇形AOB中，∠AOB=60°，C为弧上的动点，AB与OC交于点P，则的最小值是_______.

变式3：已知a·b=0，向量c满足（c-a）·（c-b）=0，|ab|=5，|a-c|=3，则a·c的最大值为________.（难度逐次递进，但与启动问题同根同源.通过习题的巧妙编排，使学生不断地思考，在思考中巩固、深化、提高）

归纳：上述“向量恒等式”使用的适用条件：共起点的向量求数量积的值或范围，在已知三角形中有一边确定或其范围一定.

说明：从本题的变换可以看出，一个问题涉及数个一维数轴式的知识点，将一个问题进行变化探究和多角度分析，可以较为高效地提高从一个典型问题辐射一类问题，即在用数量积求取值范围相关问题时如何利用向量恒等式这是新课程教学在指导我们解题教学时需要注意的.

境界三：三维空间式解题

如果说将高中数学解题教学的基本功和常规问题熟练化做得非常完美的话，也就是上述两个纬度的解题做到了比较完善，笔者认为还能对学生更好的指导来自数学思想方法的教学.课程标准制定参与者北师大张英伯教授对于数学解题教学给出了这样的总结性话语：中学数学要传授解题，但更要传授在这背后所呈现的思想方法，我认为能力性的思想方法主要是转化与化归思想，这一思想方法是贯穿中学数学教学的始终，除此之外诸如函数与方程思想、数形结合思想、分类讨论思想等知识性的思想方法属于第二层次，中学数学教学中教师要多给予这种转换的指导，有利于学生问题解决能力的培养以及数学解题能力的提高.因此，笔者将思想方法渗透的解题教学称之为三维空间式的解题，站在系统的高度解决数学问题，做到轻沙走马路无尘. 2）2+（y-2）2=2，这是一个以点（2，2）为圆心、√2为半径的圆，作出图像（如图1），从图中可知两向量、的夹角的取值范围是

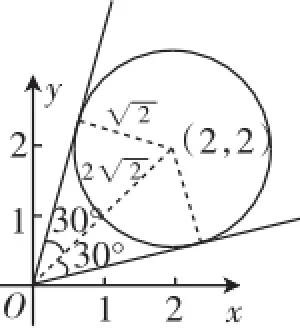
图1

说明：反观本题的解决并非太难，甚至很多学生都觉得不过如此，按照自身实际能力也能解决.但问题真正难在哪里？难在具备数学思想方法的眼光！抛开问题给出的答案，笔者曾经尝试过，四十五位同学中具备利用正确的数学思想方法解决问题的人不超过五位，可见学生往往在问什么想什么！根本不可能站在系统的高度思考一个问题.反思本题，用到的数学基础知识并不难，知识之间的链接整合也不是触摸不到，难的是无法找到合适的切入点找到正确的思想方法，进而选取最简捷的数形结合方式.

总之，新课程数学解题教学不能仿似传统解题教学以大量训练替代，而且课程改革改变了数学解题教学的理念，让教师不断从效率角度提升解题教学，笔者经过思考认为层层递进、螺旋式上升的解题教学是提升学生问题解决能力的关键.从知识点的熟练扎实，到知识横纵整合，到最后从思想方法的高度进行渗透，将优秀学生的问题解决能力进行更好的提升，久而久之形成体系的解题教学才能成为适应新课程的高效教学.

1.罗增儒.数学解题导论［M］.西安：陕西师范大学出版社，2002.

2.张奠宙.再谈数学双基［J］.数学教学，2013（8）.

3.金凤明.庖丁解牛与数学解题［J］.上海中学数学，2008（4）.A