☉福建师范大学附属中学 沈春林

一道北约自招试题的解法与源流研究

☉福建师范大学附属中学 沈春林

2014年北约自主招生压轴题与不等式有关，形式简约，表面看似接近中学教学实际，然而细细品味会发现其意蕴深刻，源远流长，这种“接地气通天庭”的试题特征在该题中体现得淋漓尽致，较好地引导着一些优秀学子钻研数学的兴趣和热忱.本文详细讨论2014年北约自主招生的压轴题的各种解法并研究其源流，为自主招生试题的研究提供一个思路和参考.

一、试题的解法研究

题目（2014年北约自主招生第10题）若xi＞0（i=

本文整理了8种解法，单从五花八门的解答中已经可以感受到试题的灵活多变及“来头不小”.

解法3：（加权均值不等式）两个数的加权均值不等式xαyβ≤αx+βy，其中x，y≥0，α，β∈［0，1］且α+β=1，多个数的加权均值不等式

解法4：（运用holder不等式）设aik≥0（i=1，2，…，m； k=1，2，…，n），xi≥0，αi∈［0，1］且（Holder不等式）.实际应用中通常取

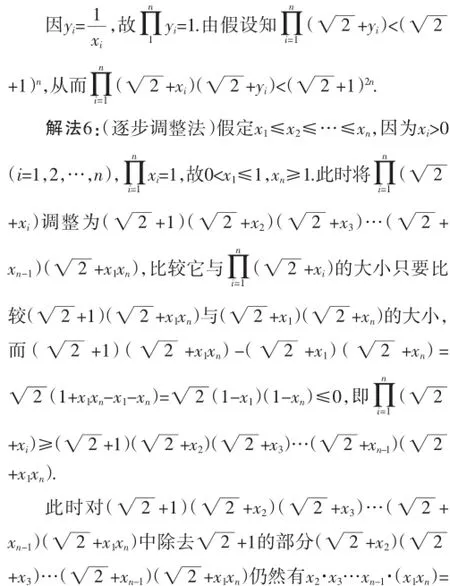
解法7：（数学归纳法）数学归纳法的实质与逐步调整法相同，简述如下：

n=1时显然命题成立，假定n=k时命题成立，即xi＞ 0命题也成立，故原命题成立.

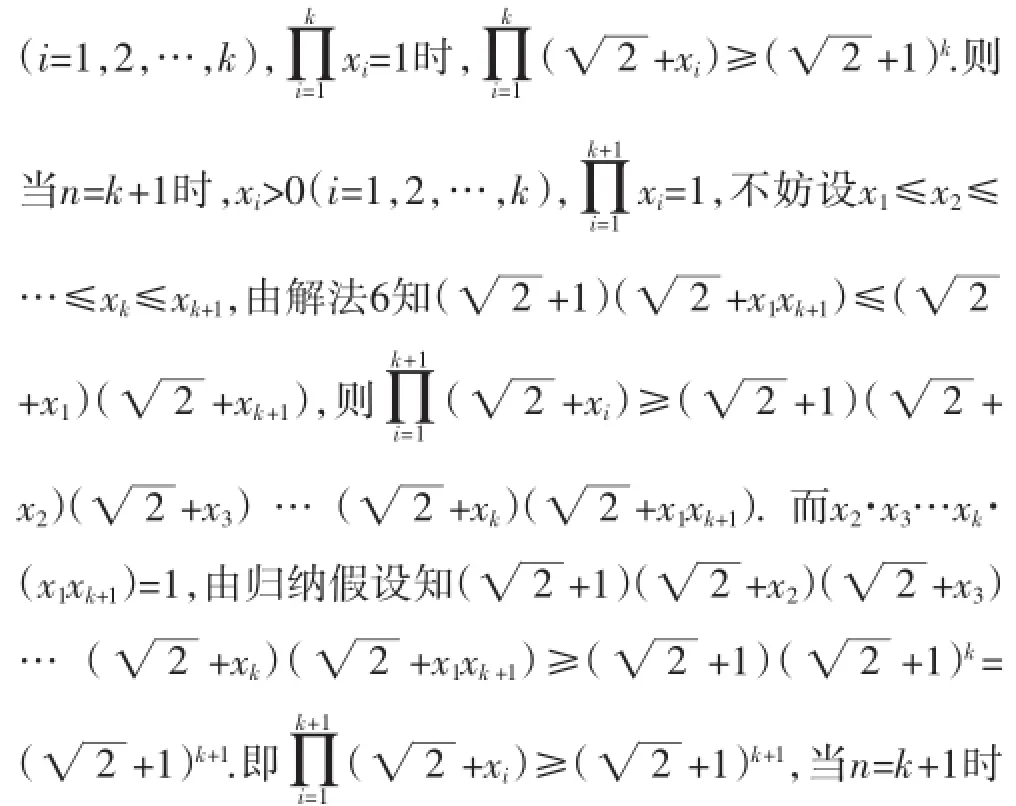
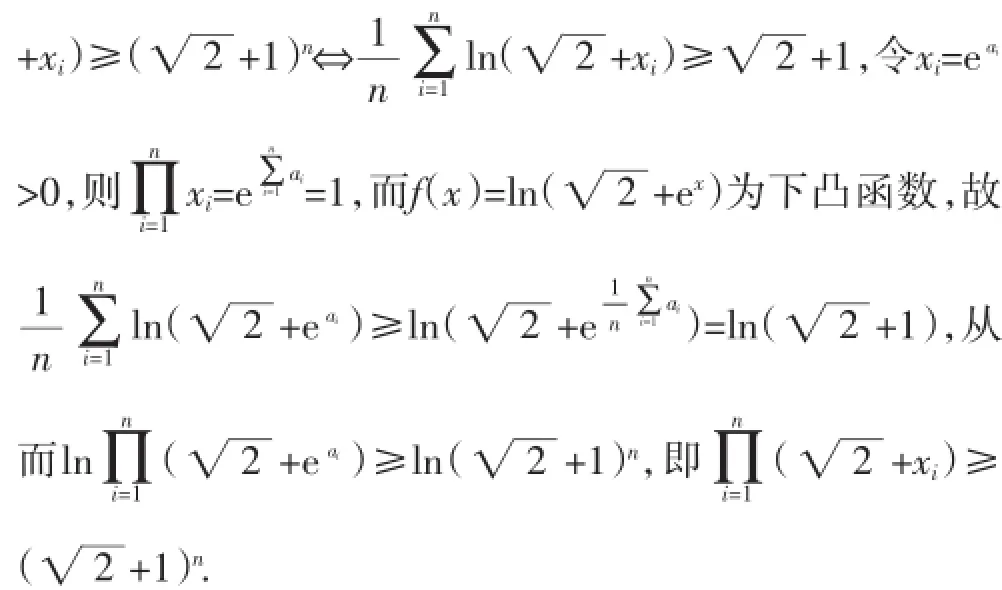
二、试题的源流研究

1.chrystal不等式

研究解答试题的方法源流是一件有意思的事情，试题的直接来源是著名的chrystal不等式，即：设ak＞0，则等式几乎与刚刚讨论的不等式完全一样了，chrystal不等式的证明也就几乎可以将上述方法不作修改地移用过来.chrystal不等式可以证明某些复杂不等式，诸如国家队选拔试题：已知5n个实数ri，si，ti，ui，vi（1≤i≤n）都大于

2.chrystal不等式的变用与加强1，其证明只需要两边取对数等价转化，再对下凸函数f（x）运用Jensen不等式即可.运用该不等式也可以证明一些复杂不等式，诸如：在△ABC中，证明：27∏cosA≤若有一个角为钝角或直角，则不等式显然成立，当△ABC为锐角三角形时，27∏cosA≤

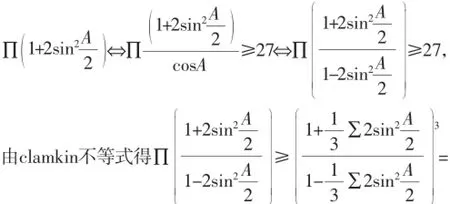
3.chrystal不等式与其他不等式的辩证关系

从上面的证明过程可以看到，证明chrystal不等式可以用Jensen不等式、逐步调整法、数学归纳法等本源性的方法，也可用均值不等式、加权均值不等式、holder不等式等重要不等式，之所以称Jensen不等式、逐步调整法、数学归纳法为本源性方法，主要是基于人们认识和学习不等式通常所遵循的认知规律和先后顺序，因为均值不等式用这三种方法均可推出，而加权均值不等式、holder不等式又可由均值不等式直接推出，也可由Jensen不等式、逐步调整法、数学归纳法等本源性的方法推出，chrystal不等式同样如此，也就是说chrystal不等式和加权均值不等式、holder不等式拥有同一个产生它们的“母亲”均值不等式，共同拥有产生它们的“奶奶级”的方法Jensen不等式、逐步调整法、数学归纳法等本源性的方法，至于用加权均值不等式、holder不等式对chrystal不等式的证明就仿佛来自“兄弟姐妹”的帮助，而在chrystal不等式的变用和加强则好似“孙子辈”自身的开枝散叶．

由此可见一个不等式证明问题，如果能够用重要不等式去给予证明，那么此不等式与重要不等式的证明是存在某种方法上的互通性和一定程度的本质一致性的，如果能够从重要不等式证明的思维策略和方法上吸取营养，定会增强我们对形形色色不等式的直观感觉能力和对其本质的透视能力.大而言之，这种既贴近中学教学实际而又包含众多数学思想方法精髓的本质性问题正是自招试题命题者的大手笔，它有效检验了数学学习者的思维积淀和知识积淀，从这道试题的解答中我们可以感受到认真审视我们的学习过程，注意对数学问题本质的理解，适当拓展，用思想和方法去统领数学知识，使其成为“源头活水”，让知识和思维同时积淀，或许这才是应对自招试题的良策.

1.厉倩．Holder不等式的再推广及应用［J］.数学通讯，2006（3）.

2.石焕南，石敏琪．对称平均值基本定理应用数例［J］.数学通报，1996（10）.F