游波，蔡志明

(海军工程大学水声工程系，湖北武汉430033)

水下目标在进行一系列战术动作时辐射瞬态信号，例如鱼雷在空投和潜射过程中产生的瞬态信号，潜艇在转向、加速时产生的瞬态信号，以及浮标声呐信号和主动声呐侦察脉冲信号等。由于潜艇和舰船吸声降噪技术的发展，声呐对水下目标稳态辐射噪声的检测愈加困难，而对瞬态信号的检测将弥补稳态信号检测的弱点，产生积极的军事效益。

瞬态信号检测技术基于多种原理。高阶谱分析方法与Power-law检测器的结合［1］抓住瞬态信号的非高斯特征，对信号先验知识要求少。基于小波变换的适应性时频检测方法［2］利用非高斯小波系数和噪声系数四阶矩的差异，进一步突出瞬态信号，但小波基函数的选择对分析结果有较大影响。希尔伯特－黄变换［3］的特征时间尺度基于信号自身特性，经验模态分解是希尔伯特－黄变换理论的核心，将信号依据不同的时间尺度分解成一系列的固有模态函数。但固有模态函数截止阶数的选择会影响模态分解结果。累积和检验方法(Page Test)［4-7］是一种基于概率特征分析的检测方法，能敏感捕捉瞬态信号出现引起的概率分布函数变化。研究表明［8］该方法性能优于Power-law检测器、短时傅里叶变换、小波变换等其他方法。

根据纽曼皮尔逊准则，利用检测性能分析方法计算门限和相关参数是实现累积和检验的关键。检测性能的数值分析方法有矩阵法和快速傅里叶变换法2种。矩阵法的量化过程由于引入了高维(约几千阶)矩阵的连乘，运算量非常大，计算精度不高。快速傅里叶变换法则将2个时间序列的卷积转化为频谱乘积的反傅里叶变换，利用快速傅里叶变换来实现每一步检验统计量概率分布的计算，在高精度要求下依然具有合理的运算量。文献［9-10］对快速傅里叶变换法的介绍仅限于简单的原理，缺乏对更新量量化范围的分析推导，也没有提及基于马尔可夫状态转移矩阵的检测概率递归计算方法，而这2个问题是利用快速傅里叶变换方法进行累积和性能分析的关键步骤。本文解决了上述问题，并将检测概率理论计算结果和蒙特卡洛仿真实验结果进行对比，吻合度好，水池和海试数据的检测结果进一步表明了累积和检验方法检测低信噪比水声瞬态信号的有效性。

1 累积和检验方法性能分析模型

1.1 高斯分布方差变化假设下累积和检验统计量

累积和检验方法检测性能与信号出现前后概率分布模型或参数的变化密切相关。由于瞬态信号的突发性和不稳定性、声信道传播特性未知等因素，概率密度模型复杂，从一般意义上可将其看作信号出现前后方差发生变化的高斯分布。

给定观测值序列X={x1，x2，…，xN}，假设瞬态信号出现前后，概率分布律从f0变化至f1，即从标准正态分布变化至方差为σ2的高斯正态分布:

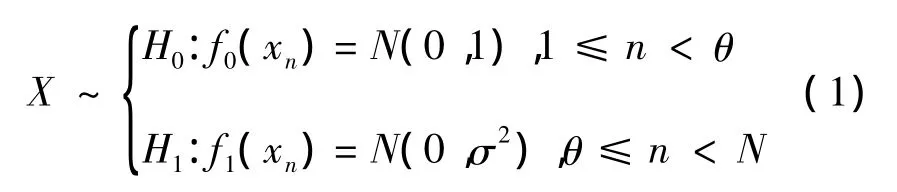
式中:变化发生点θ未知。依据最大似然比准则［11］得到累积和检验的对数似然比统计量写成:

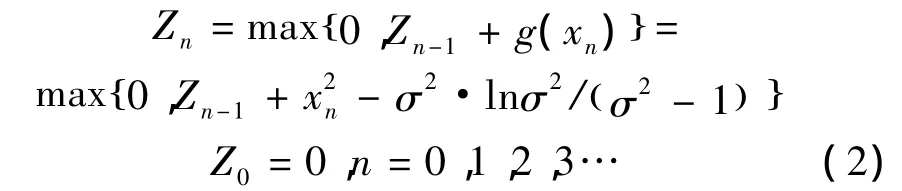
式中:g(xn)称为非线性量或更新量，可写成g(xn)=x2n－b，b=σ2·lnσ2/σ2－( 1)为偏差。g(xn)要求满足:累积和检验实际上是一种基于最大对数似然比准则的序贯检测方法。设0和h分别为上、下门限，检测过程可描述为

1.2 模型原理和量化方法

FFT法利用马尔可夫过程来关联被检测序列在不同时刻状态之间统计联系。因此在该序列以及更新量可能值域范围进行量化，建立马尔可夫状态转移矩阵是计算检测概率的必要前提条件。

由式(2)得到n时刻Zn的概率分布律φn(z)等于n－1时刻Zn－1概率分布律fn－1(z)与更新量g(xn)概率分布律fg(z)的卷积，由于2个时间序列的卷积等同于频谱乘积的反傅里叶变换，上述关系可表为

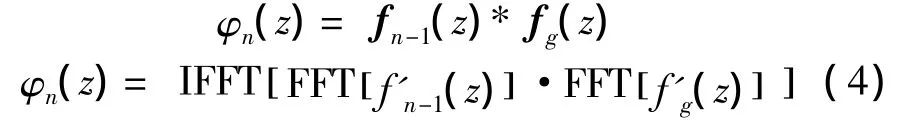
将复杂的卷积运算转化为快速离散傅里叶变换的乘积是快速傅里叶变换方法的主要思想。若检测过程能持续到n时刻，则对φn(z)(0＜z＜h)进行归一化操作后，n时刻Zn的概率分布律fn(z)可表为

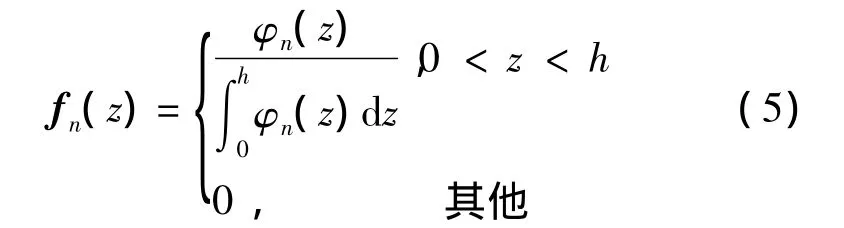
式中:fn(z)、fg(z)为矩阵，分别表示检验统计量Zn和更新量g在可能值域范围每个量化点的概率。将上式(5)进行递归运算，可计算任意时刻检验统计量概率分布律。

一般可假设检测过程从H0假设下的零状态开始。下面以方差发生变化的高斯分布假设为例分析更新量g(xn)的量化方法。由契比雪夫不等式［12］有为数学期望，ε为任意正数。令μ=0，ε=10σ，则X以不小于99% 的 概 率 分 布 在 10σ 的 范 围，令更新量g(xn)=yn=－b，则在H0和H12种假设下yn分布范围的上限分别写为

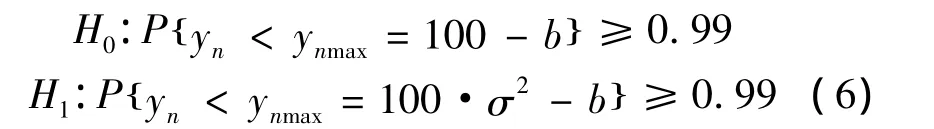
yn的下限为yn≥－b。设yn的量化范围为［hl，hh)，检测门限为h，下门限可表为hl= max(－h，－b)，上门限可表为hh=max(h，ynmax)。ynmax在H0和H1假设下的取值参见式(6)。设量化阶数为N，量化步长为Δ=(hh－hl)/N，每一个量化点可表示为yi=g(xi)=hl+i·Δ，i=1，2，…，N。由雅可比行列式，经过计算得更新量yn=g(xn)服从分布:

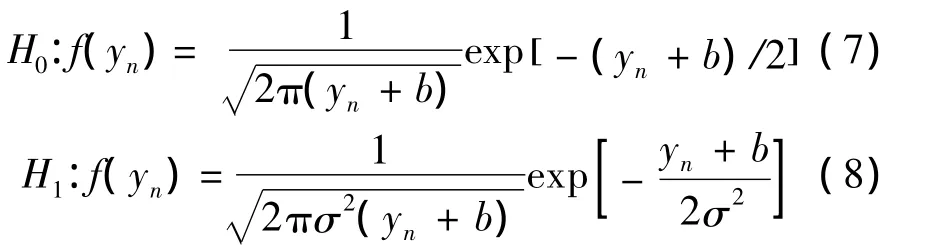
将式(7)、(8)代入yn=g(xn)在每一个量化点的值计算可得n时刻更新量等于各个量化值的概率，即fg(z)=Pr{g(xi)=yi}，组成向量，代入式(4)、(5)即可进行递归运算。文献［10］的量化范围直接取为［－h，h)，这样做会导致量化值域分布范围的不准确，也会直接影响更新量概率分布律fg(z)的精度，从而给后面的参数估计带来影响。特别是当信号点数很少时，门限给出的量化范围小于更新量可能的数值分布范围，在一定的虚警和检测概率下无法计算出门限和方差。

1.3 利用快速傅里叶变换方法计算检测概率

H1假设下的检测一般考虑2种初始状态，一是零初始状态，即f0(z)=δ(z)，二是在H0假设下已经进入的稳定状态fss(z)。累积和方法检测过程中的置零复位操作(如式(2))意味着下一时刻检测初始状态的改变，因而置零次数直接影响更新量概率分布律的计算。在计算检测概率时，一般将H1假设下超门限检测具体分成2种情况:1)检验统计量未经任何置零复位操作超门限，置零次数k为零;2)检验统计量经过k(k≥1)次置零超门限。

在N个样本长度内未置零复位操作而发生的检测概率可写为

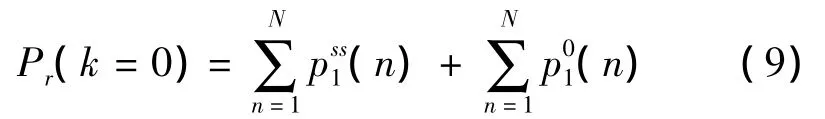
另假设在被检测的m(1≤m≤N－1)长序列中有k次置零复位操作，1≤k≤m，记p(k)0(m)为k次置零复位(检测判决为无信号，记为0)的概率。序列中剩余(N－m)个点从0状态开始，检测结果为有信号。因而发生k≥1次置零操作而超门限检测概率可写为

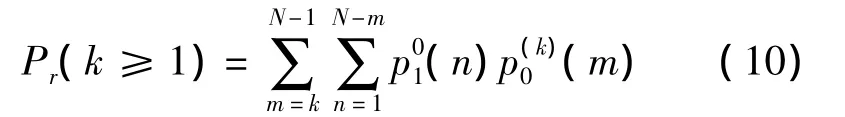
求解k次置零的概率p(k)0(m)，需要用到状态转移矩阵的递归求解过程。这个问题在文献［7-8］中并没有提及。如图1所示，设检测N长序列，k次置零操作发生在m点范围内，即1≤k≤m≤N－1。必须指出的是，k次置零操作的最后一次应发生在第m点，否则这k种置零组合方式会与更小长度序列的k种置零组合方式重合，出现重复计算的情况。其余(k－1)次置零操作可能发生在(m－1)个点的范围里，发生概率p(k－1)0(m－1)是(k－1)次独立置零概率乘积的多种组合方式之和。

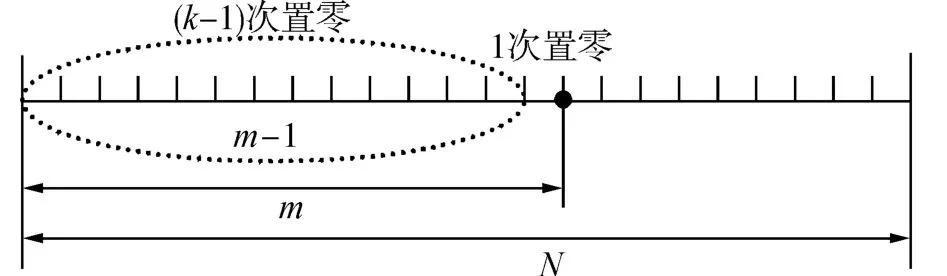
图1 检测概率计算的递归示意图Fig.1 Illustration of the recursive calculation of Pd

建立H1假设下稳定初始状态时的状态转移矩阵C1:

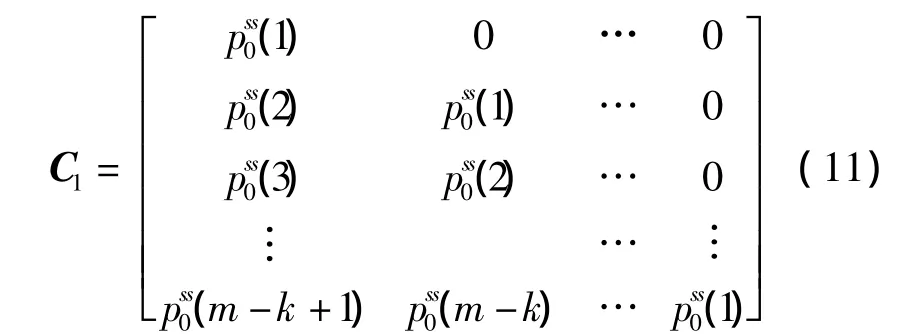
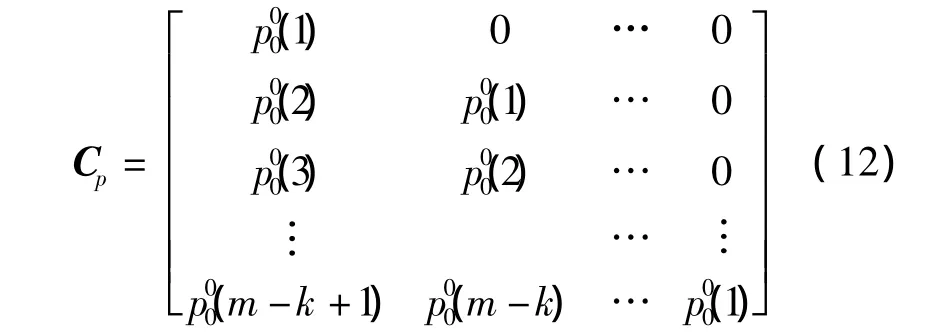
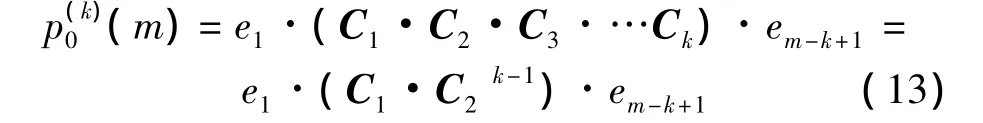
式中:ei表示1·(m－k+1)维，在第i点上为1，其余位置为0的向量。式(13)可实现图1所示k次置零概率的求解过程。将式(13)代入式(10)，得到稳定初始状态时发生k≥1次置零操作而超门限检测概率，再结合式(9)，最终得到在稳定初始状态时瞬态信号持续过程中发生的检测概率Pd:

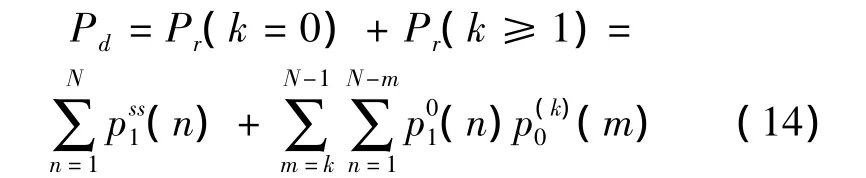
当初始状态为零时，瞬态信号持续过程中发生的检测概率Pd写作:

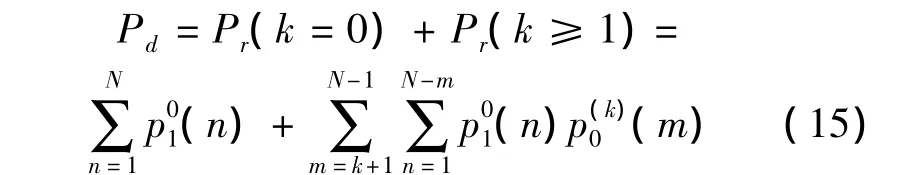
在Pr(k≥1)的运算过程中，第1点虽为零，但不计入置零操作次数，检测m个点发生置零操作的次数1≤k＜m≤N－1，其余推导过程类似。瞬态信号持续过程中发生的检测概率应为式(14)和(15)之和。关于在瞬态信号结束后出现的延迟检测概率计算详见文献［7］。

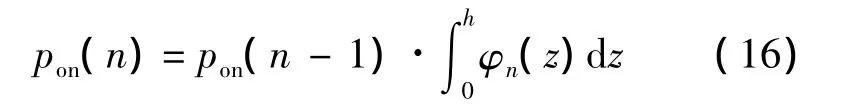
在n时刻结束且检测为无信号的概率可表为

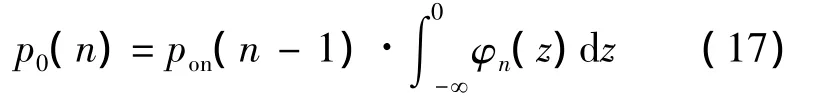
在n时刻结束且检测为有信号的概率可表为

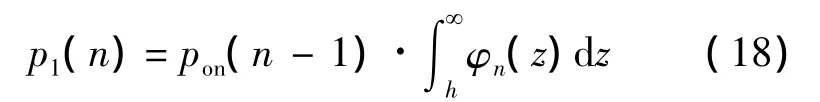
式中:pon的初值pon(0)设为1。式(16)～(18)体现了累积和算法序贯检测的特征。其中n时刻Zn的概率分布律φn(z)利用快速傅里叶变换法由式(4)和式(5)递归计算得到。前面所提及H0下的稳定状态是指在H0假设下，当检测过程进行一段时间后仍未做出判断，即可认为进入了稳定状态［10］。稳态时检验统计量Zn的归一化概率分布律可表为

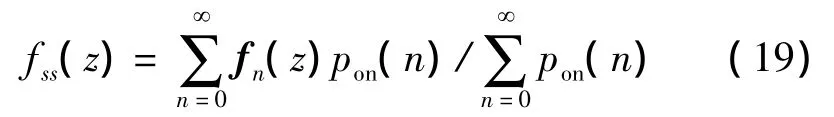
2 理论计算与仿真实验结果比对

图2为当门限为40，方差为1.36时检测概率理论计算结果和10 000次蒙特卡罗仿真结果，两者的结果非常接近。图3表示当虚警间的平均间隔T－=104s，Pd=0.6时，在纽曼皮尔逊准则下利用上述虚警概率和检测概率的模型，寻优搜索计算得到的检测门限h和方差σ2随瞬态信号长度的变化图。

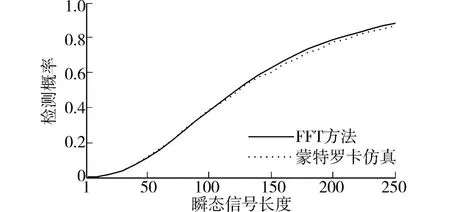
图2 方差变化的高斯分布下检测概率理论计算结果和蒙特卡罗仿真结果比较Fig.2 Comparison between the theoretical result and the Monte Carlo simulation result in Gaussian shift-in-variance transient problem

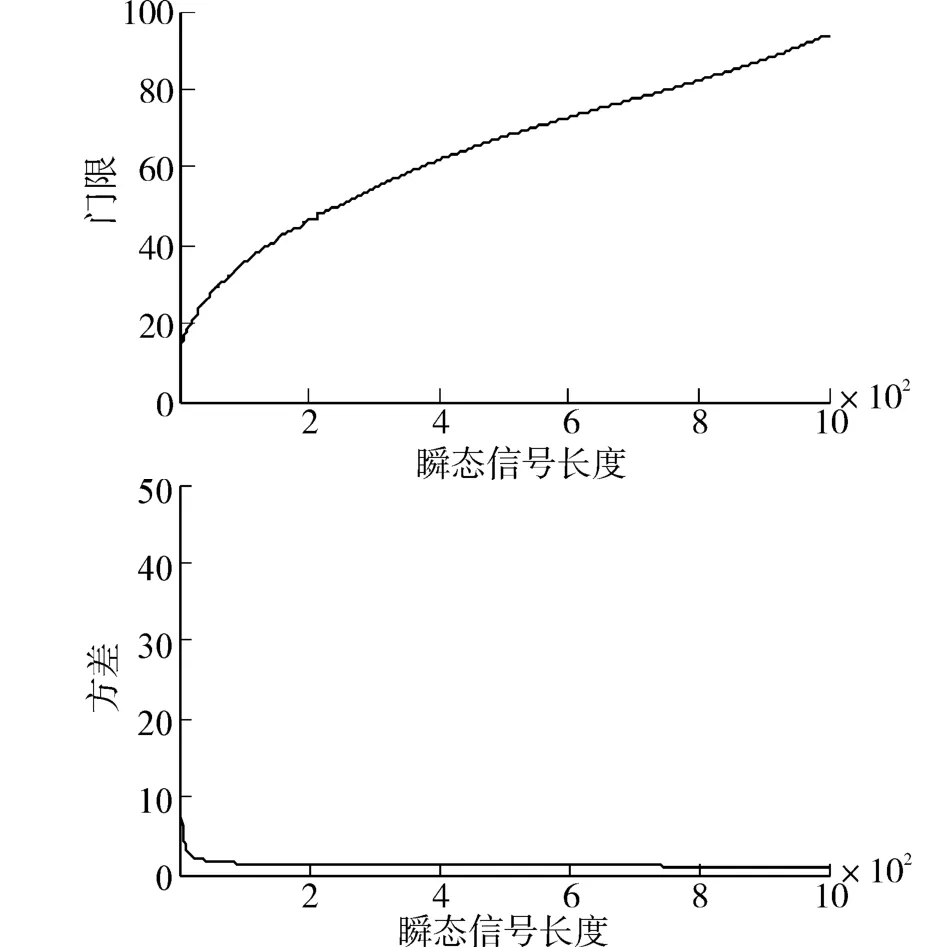
图3 当=104，Pd=0.6时快速傅里叶变换方法计算所得检测门限和方差随瞬态信号长度的变化Fig.3 Illustration of the threshold and variance calculated for different transient signal lengths with =104and Pd=0.6.

3 水池实验和海试数据验证

图4为在消声水池中采集到的重物落水瞬态信号，信号主要能量分布在0.2～0.5 s，频率分布在100～210 Hz范围内，采样率为800 Hz，瞬态信号长度为200个点。将0.3 s的信号以－10 dB叠加到高斯白噪声上，信号持续时间为0.725 s～1.025 s。根据图3的计算结果，算法参数设定为门限47.499，偏差1.120 9。图5累积和检验结果中在0.725～1.025 s处信号清晰，可见该方法能有效检测低信噪比水声瞬态信号。

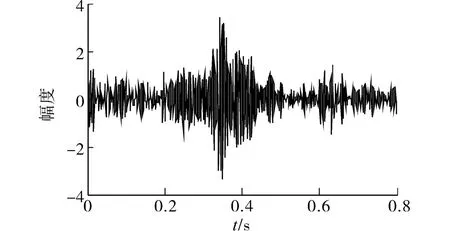
图4 水池采集信号滤波后波形Fig.4 The transient signal waveform collected after filtering

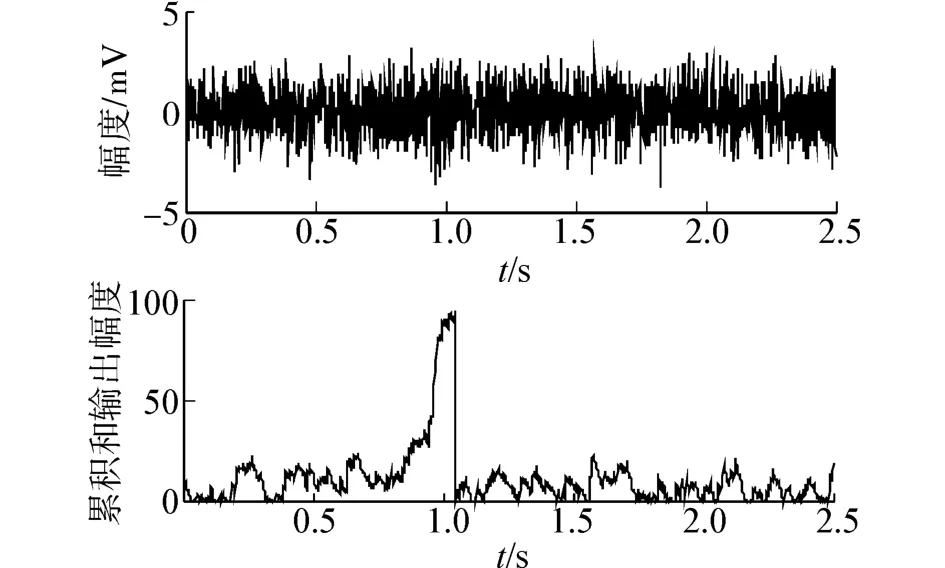
图5 瞬态信号按－10 dB重新加入后的波形及累积和检验统计量输出波形Fig.5 The detected waveform with transient signal of－10 dB and the result of the page test

2014年6月舟山外海标定声源拉距试验。图6是波束形成后能量积分(2 s)检测和被动累积和检测结果比对。

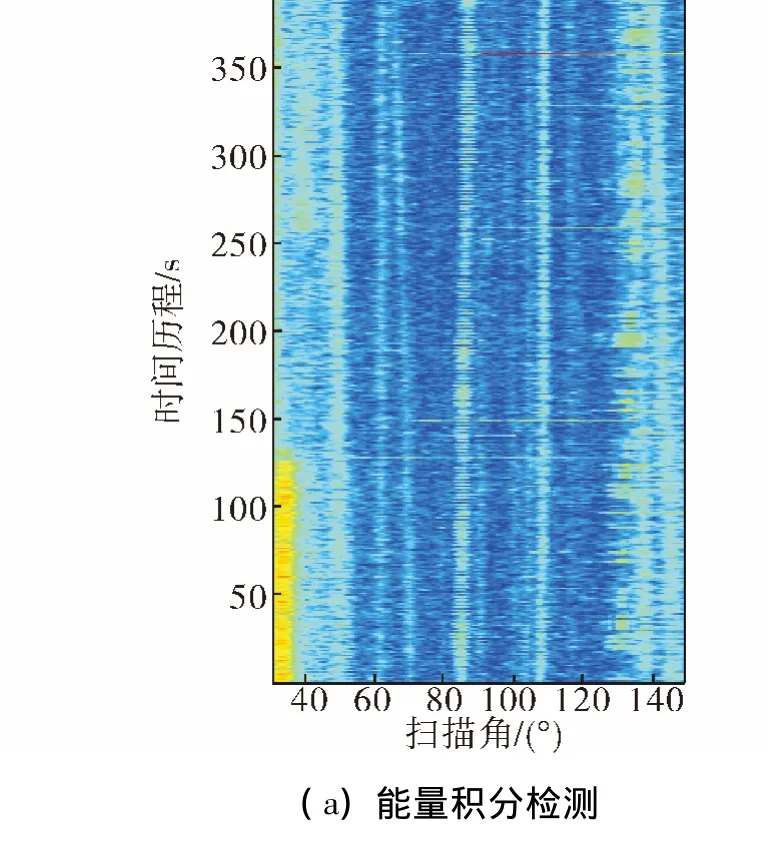
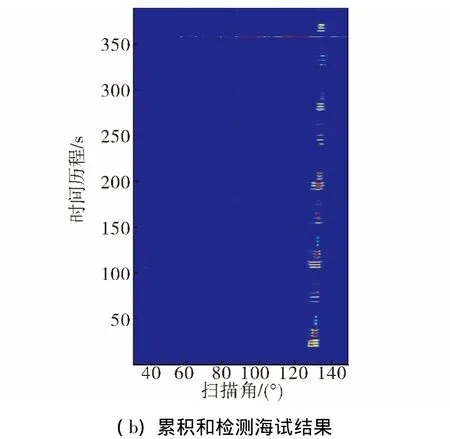
图6 波束形成后能量积分检测和累积和检测海试结果比对Fig.6 Comparison between the results of the energy integral test and the Page Test using the data collected in the sea

声源船距离15.97 km，声源是脉宽为2 s的低频脉冲信号。试验背景为多艘船只的稳态噪声干扰。可见累积和检验算法能抑制稳定噪声干扰，有效检测瞬态信号，信噪比增益明显。

4 结论

本文基于马尔可夫状态转移思想，推导了被检测序列在高斯分布方差变化假设下快速傅里叶变换法量化值域确定方法、更新量概率分布律的计算方法和检测概率的递归计算方法。在验证部分，将基于快速傅里叶变换法的检测概率理论计算结果和蒙特卡洛仿真实验结果相比较，吻合度好。水池和海试数据的验证结果表明，利用本文建立的性能分析模型寻优搜索出的门限和方差，累积和检验方法能有效检测低信噪比的水声瞬态信号。

当然对水声瞬态信号而言，高斯分布方差发生变化的假设显然不够准确，对各种瞬态信号更为准确的概率密度模型的建立将有助于提高检测性能。这也是下一步的研究方向。

［1］吕俊军，吴国清，杜波.非高斯水声瞬态信号Power-Law检测［J］.声学学报，2004，29(4):359-362.

LYU Junjun，WU Guoqing，DU Bo.Non-Gaussian underwater transient signals detection using power-law detector［J］.Acta Acoustica，2004，29(4):359-362.

［2］CORNEL L，ANDRE Q.Transient signal detection using overcomplete wavelet transform and high-order statistics［C］//ICASSP2003.［S.l.］，2003.

［3］吕成刚.水下瞬态信号特性获取与分析［D］.哈尔滨:哈尔滨工程大学，2009:44-51.

LYU Chenggang.Characteristic acquiring and analyzing of underwater transient signal［D］.Harbin:Harbin Engineering University，2009:44-51.

［4］ABRAHAM A D，WILLETT P.Active sonar detection in shallow water using the Page Test［J］.IEEE Trans on Aerospace and Electronic System，2002，33:1225-1229.

［5］WANG Zhen.New approaches to transient detection and signal segmentation［D］.Storrs:University of Connecticut，2002:72-83.

［6］游波，蔡志明.累积和检验算法中的反馈机制研究［J］.电子学报，2010，38(6):1434-1437.

YOU Bo，CAI Zhiming.On feedback mechanism of the page test［J］.Acta Electronica Sinica，2010，38(6):1434-1437.

［7］游波，蔡志明.一种估计主动声呐回波扩展时间的有效方法［J］.电子学报，2012，40(12):2223-2556.

YOU Bo，CAI Zhiming.An effective method to estimate spreading time of active sonar echoes［J］.Acta Electronica Sinica，2012，40(12):2223-2556.

［8］WANG Zhen，WILLETT P.A performance study of some transient detectors［J］.IEEE Transaction on Signal Processing，2000，48(9):2682-2685.

［9］游波，蔡志明.累积和算法应用于主动声呐检测时的性能分析［J］.海军工程大学学报，2009，21(6):80-83.

YOU Bo，CAI Zhiming.Analysis of performance of the Page's Test as used to detect active sonar signals［J］.Journal of Naval University of Engineering，2009，21(6):80-83.

［10］HAN Chunming，WILLETT P.Some methods to evaluate the performance of Page'sTest as used to detect transient signals［J］.IEEE Trans on Signal Processing，1999，47: 2112-2127.

［11］濮晓龙.关于累积和(CUSUM)检验的改进［J］.应用数学学报，2002，26(2):225-241.

PU Xiaolong.The improvement of the CUSUM test［J］.Acta Mathematicae Applicatae Sinica，2002，26(2):225-241.

［12］盛骤，谢式千.概率论与数理统计［M］.北京:高等教育出版社，2008:36-43.

SHENG Ju，XIE Shiqian.Probability and mathematical statistics［M］.Beijing:Higher Education Press，2008:36-43.