均匀性模式及其在试验设计中的应用
2015-03-21汪政红2
覃 红, 汪政红2,*
(1.华中师范大学 数学与统计学学院, 武汉 430079; 2.中南民族大学 数学与统计学学院, 武汉 430074)
均匀性模式及其在试验设计中的应用
覃 红1, 汪政红2,1*
(1.华中师范大学 数学与统计学学院, 武汉 430079; 2.中南民族大学 数学与统计学学院, 武汉 430074)
均匀性是一个几何概念,通常采用不同的偏差来度量设计的均匀性.但偏差的度量侧重于总体,即考虑所有投影子设计的均匀性总和,而根据效应排序原则,低维投影均匀性应该比高维投影均匀性更重要,基于这一思想许多学者提出了类似于字长型的均匀性模式的新概念,并用它来度量设计的各阶投影均匀性.该文对均匀性模式的文献进行了综述,并给出均匀性模式及相关的最小低阶投影均匀性准则的统一定义.该文还对最小低阶投影均匀性准则与其他各种设计筛选准则之间的联系及其在补设计中的应用等进行了综述,这些联系表明最小低阶投影均匀性准则与因子设计中的广义最小低阶混杂准则、正交性准则、V准则、最近平衡性准则、设计效率准则、E(s2)准则之间是相互等价的,这些准则彼此之间可以互相支持,因此揭示了均匀设计和因子设计之间的内在关系.此外,该文还对现有文献中均匀性模式的下界进行了综述,并将达到下界的MPU设计案例罗列出来以方便实际工作者使用.
均匀性模式; 最小低阶投影均匀性; 广义最小低阶混杂; 正交性; 补设计; 下界
统计试验设计方法有许多种,其中由方开泰教授和王元院士提出的均匀设计[1-2]被用于计算机仿真试验和模型未知的稳健试验,成功地应用到国防、工农业、医院、高新技术创新等诸多领域,推动了国民经济和社会的发展,为人类的进步和科学研究的发展做出了突出贡献.随着均匀设计的应用不断被推广和深入,相应有关均匀设计的理论也在不断被建立和完善.与此同时,均匀性也被用作一种准则来比较不同的因析设计,并且发展成为目前最流行的设计筛选准则之一.均匀性准则要求设计具有最好的均匀性,即要求试验点均匀地分布在试验区域里.文献里一般采用数论方法(或伪蒙特卡罗方法)中的偏差来衡量设计的均匀性,这就是所谓的偏差准则.偏差的定义方法有很多种,最早采用的是星偏差[3],在数论方法的几本专著中(如文献[4-5]等)均对星偏差作了重要介绍.但星偏差有不少缺点,如计算复杂,忽略了设计的低维投影均匀性因而对均匀性不够灵敏等.为了克服星偏差的诸多缺点,Hickernell[6-7]利用希尔伯特空间的再生核概念提出广义Lp星偏差,并将古典的诸偏差表示成统一的形式,又从这个统一形式出发定义了许多新偏差,例如中心化L2偏差、可卷型L2偏差、离散偏差等等.这些偏差考虑到设计点集在所有维度的投影均匀性,可以克服星偏差的缺点,因而在试验设计中得到了广泛应用.其中中心化L2偏差、可卷型L2偏差是定义在连续区域上的,可以考察因子是连续变量的设计的均匀性,因此对试验点有更多的选择,适合用来构造均匀设计;离散偏差是基于Hammin距离定义的,适用于度量因子取离散水平的设计的均匀性,但只能判断设计中对应分量是否相等,因而用离散偏差来度量多水平因析设计的均匀性有一定的局限性.为了改进离散偏差的这一不足,Zhou,Ning和Song[8]从Lee距离出发定义了Lee偏差,Chatterjee和Qin[9]定义了广义离散偏差.各种偏差的定义及详细介绍可以参见文献[10-11],这里只简要介绍本文所关心的几种偏差及其计算公式.
当试验区域可转化为χ=[0,1]s时,设d={x1,…,xn}为试验区域χ上的n个试验点,则设计d可以表示为一个n×s的矩阵:
1)中心化L2偏差
中心化L2偏差的详细定义可参见文献[6],这里仅简要列出其计算公式.记设计d的中心化L2偏差值为D(d;1),其中1为一种再生核函数,则
当试验区域为离散的格子点时,即χ=χ1×…×χs,χj={0,1,…,qj-1},仍假设d={r1,…,rn}=(rik)n×s为试验区域χ上的n个试验点,第j个因子有qj个水平0,1,…,qj-1.
2)离散偏差I
Hickernell和Liu[12]及Qin和Fang[13]等利用一种再生核函数2定义了一种离散偏差,本文称之为离散偏差I.记设计d的离散偏差I值为D(d;2),则
其中,a>b>0,当rij=rkj时,δrijrkj=1,否则为0.
3) Lee偏差
Zhou,Ning和Song[8]利用Lee距离定义了Lee偏差,记设计d的Lee偏差值为D(d;3),则
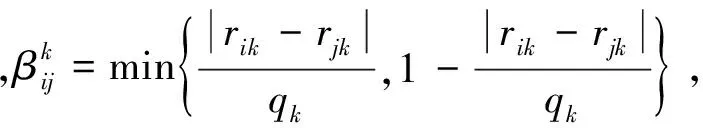
4)离散偏差II
Hickernell和Liu[12]及Qin和Ai[14]等利用另一种再生核函数4定义了一种离散偏差,本文称之为离散偏差II.记设计d的离散偏差II值为D(d;4),则
其中,0<γ<1.
从Fang和Mukerjee[15]发现两水平正规部分因析设计的中心化L2偏差与字长型之间的解析关系开始,偏差准则与其他设计筛选准则之间的联系就不断被发现.如Fang,Ma和Mukerjee[16]很快就将文献[15]中的结论推广到了非正规部分因析设计的情形,且除中心化L2偏差之外同时还讨论了可卷型L2偏差及对称化L2偏差;之后随着各种不同偏差的提出,越来越多的文献都表明均匀设计与因析设计的统计推断非常相关,如文献[12-14,17-20]等分别讨论了用于比较对称因析设计或非对称因析设计的偏差准则与其他设计筛选准则如广义最小低阶混杂(Generalized minimum aberration,GMA)、最小低阶矩混杂(Minimum moment aberration,MMA)等准则之间的关系.偏差准则侧重于度量设计在所有维度上的总的均匀性,即考虑所有投影子设计的均匀性总和,低阶投影子设计和高阶投影子设计对总体均匀性的贡献被认为是一样的.但是按照因子设计中“效应稀疏原则[21]”的要求,应优先考虑设计的低阶投影均匀性.于是,Hickernell和Liu[12]基于统一的偏差形式定义了投影偏差型(projection discrepancy pattern)的概念,用来度量设计的各阶投影均匀性,投影偏差型不仅具有偏差的通用性,而且还具有字长型的优点.此外,他们还证明了以一个特殊的核函数产生的偏差为基础的投影偏差型就是广义字长型[22],这说明投影偏差型具有更广泛的研究价值.序贯最小化投影偏差型即为最小低阶投影均匀性(minimum projection uniformity)准则,简称MPU准则.相比于偏差准则,MPU准则对均匀性的度量更精确,更合理,并且具有自身的特点,因而近年来也引起了众多关注,如文献[18,23-25]等讨论了两水平设计MPU准则的统计性质,文献[26-27]等讨论了高水平的对称因子设计MPU准则的性质,文献[19,28-30]等讨论了不同类型的混水平设计MPU准则的统计性质.
本文的主要目的就是总结均匀性模式及MPU准则自提出以来在试验设计中的主要研究结果和最新进展.
1 均匀性模式及MPU准则
1.1 均匀性模式的统一定义
用D(d;)表示设计d的由再生核生成的偏差值,用dω表示设计d的某一j维投影子设计,用D(j)(d;)表示设计d的所有j维投影子设计dω的D(d;)偏差值总和,即则D(j)(d;)度量了设计d的j维投影均匀性,D(j)(d;)值越小,设计d在j维的投影均匀性就越好.
定义1假设设计d包含有s个因子,称向量
UP(d;
为设计d基于偏差D(d;)的均匀性模式(uniformity pattern).
为了方便起见,下面分别介绍四种不同的均匀性模式及其计算公式.
1.1.1 基于中心化L2偏差的均匀性模式UP(d;1)Fang和Qin[18]针对二水平设计给出了基于中心化L2偏差的均匀性模式的计算公式,假设设计d∈(n;2s),对任意1≤i≤s,则
其中,u为{1,2,…,s}的一个非空子集,
注意到,

此外,Qin和Chatterjee[28]一文中又针对一类d∈(n;p×2s)设计给出了基于中心化L2偏差的均匀性模式的计算公式,
其中,
c(p,s,i)=
1.1.2 基于离散偏差I的均匀性模式UP(d;2) Qin,Wang和Chatterjee[27]针对q水平设计d∈(n;qs)给出了基于离散偏差I的均匀性模式的如下计算公式:设ω为{1,…,s}的一个势为i的非空子集,dω为设计d的对应的i维投影子设计,1≤i≤s,则
其中,dω(k1k2)表示投影设计dω的第k1行与第k2行之间的Hamming距离.
1.1.3 基于Lee偏差的均匀性模式UP(d;3) Qin,Wang和Chatterjee[29]针对二、三混水平设计d∈(n;2s1×3s2)给出了基于Lee偏差的均匀性模式的如下计算公式:设dω为设计d的任一i维投影子设计,1≤i≤s,则

1.1.4 基于离散偏差II的均匀性模式UP(d;4) 汪政红[30]针对非对称设计d∈(n;q1×…×qs)给出了基于离散偏差II的均匀性模式的定义.设dω为设计d的任一i维投影子设计,1≤i≤s,则i维投影偏差定义为:
此外,Hickernell和Liu[12]与Liu,Fang和Hickernell[19]针对非对称因子设计d∈(n;q1×…×qs)给出了如下i投影偏差的计算公式:
D(i)(d;5)=
(1)
1.2 MPU准则
定义2设向量UP(d;)=(D(1)(d;),…,D(s)(d;))为设计d基于某种偏差D(d;)的均匀性模式.设d1和d2为任意两个具有相同试验次数、因子个数和水平数的设计,r是使得D(r)(d1;)≠D(r)(d2;)的最小正整数.如果D(r)(d1;) MPU准则以偏差准则为基础,但优于偏差准则,能更全面合理地比较不同设计在均匀性方面的差异;在形式上这个准则类似于最小低阶混杂(Minimum aberration,MA)准则[31],后者从混杂性方面区分设计,而前者从几何角度区分设计.二者看似不相干,实则密切相关,如Fang和Mukerjee[15],Fang,Ma和Mukerjee[16],Qin和Fang[13]等均发现了各种偏差与(广义)字长型(Generalized word-length pattern,GWP)之间存在着解析关系,下面来分析MPU准则与其他准则之间的联系. 2.1 MPU准则与GMA准则之间的联系 定义3设d1和d2为任意两个具有相同试验次数、因子个数和水平数的设计,r是使得Ar(d1)≠Ar(d2)的最小正整数.如果Ar(d1) Hickernell和Liu[12]给出了MPU准则与GMA准则之间的如下关系: 定理1考虑设计d∈(n;q1×…×qs),则(1)式中的D(i)(d;5)=Ai(d),即MPU准则与GMA准则等价.特别地,对二水平设计,MPU准则还与Tang和Deng[33]提出的最小G2准则等价. Fang和Qin[18],Qin,Wang和Chatterjee[27,29]等也分别给出了不同形式的均匀性模式与广义字长型之间的解析关系,进一步说明MPU准则与GMA准则是一致的.具体的结果总结如下. 定理2对以下三种情形,MPU准则与GMA准则完全一致,即序贯最小化均匀性模式等价于序贯最小化广义字长型: 1) 对设计d∈ 2) 对设计d∈(n;qs),1≤i≤s, 3) 对设计d∈(n;q1×…×qs),1≤i≤s, 2.2 MPU准则与正交性准则之间的联系 Fang和Qin[18],Qin,Wang和Chatterjee[27]等均指出均匀性模式和强度之间具备如下关系. 定理3 1)对设计d∈(n;2s),则d的强度为t当且仅当D(g)(d;1)=0,1≤g≤t,同时D(t+1)(d;1)≠0; 2) 对设计d∈(n;qs),则d的强度为t当且仅当D(g)(d;2)=0,1≤g≤t,同时(t+1)(d;2)≠0; 3) 对设计d∈(n;2s1×3s2),则d的强度为t当且仅当D(g)(d;3)=0,1≤g≤t,同时D(t+1)(d;3)≠0; 4) 对设计d∈(n;q1×…×qs),则d的强度为t当且仅当D(g)(d;4)=0,1≤g≤t,同时D(t+1)(d;4)≠0. Fang和Qin[18],Qin,Wang和Chatterjee[27]还发现不同的均匀性模式与向量B(d)之间具有如下解析关系: 定理4 1) 对设计d∈(n;2s),1≤g≤s,有 2) 对设计d∈(n;qs),1≤g≤s,有 3) 对设计d∈(n;2s1×3s2),1≤g≤s,有 其中,S={(i,j)≠(0,0)|0≤i≤s1,0≤j≤s2}. 4) 对设计d∈有 2.3 MPU准则与设计效率准则之间的联系 在试验的初级阶段,试验者对响应与因素之间的模型关系往往所知甚少,因而在模型不确定的情况下使用一个表现稳健的设计十分重要.我们知道均匀设计是将试验点均匀地散布在试验区域,因而稳健性很好,那么,MPU设计是否也具备类似的稳健性质呢? 对于二水平部分因析设计,Qin,Zou和Zhang[25]研究了均匀性模式UP(d;1)与设计效率之间的关系,并发现由Cheng,Deng和Tang[35]在模型不确定的前提下所提出的设计效率的度量完全可以用均匀性模式UP(d;1)中的前4个分量D(1)(d;1),…,D(4)(d;1)来线性表示.由此说明,均匀性模式UP(d;1)可以作为文献[35]中设计效率这一概念的替代,并且均匀性模式UP(d;1)的计算比设计效率容易得多.具体结果可见文献[25]. Mandal和Mukerjee[34]已将文献[35]中设计效率准则由二水平推广至任意非对称因析设计情形,在此基础上,汪政红[30]研究了任意等水平设计的均匀性模式UP(d;2)与设计效率之间的关系,同样也发现设计效率的度量可以由均匀性模式UP(d;2)中的前4个分量线性表示.这意味着,MPU设计将也是设计效率准则下的最优设计. 2.4 MPU准则与其他设计筛选准则之间的联系 在试验设计的理论和应用研究中,基于各种不同的目的和需求,试验设计学家除了上述介绍的设计筛选准则外,还提出了其它不同的选择最优设计的设计筛选准则,如为了研究二水平设计的投影性质,Tang[36]提出用一个V-向量(V1(d),…,Vs(d))来度量不同维度上的投影性质,其中Vi(d)可以通过公式 (2) (3) 结合定理2及(2)、(3)式,Zhang和Qin[23]得到MPU准则与V-准则、最近平衡性准则之间的如下关系: 定理5对d∈(n;2s),1≤i≤s,有 超饱和设计是一类非常重要的非正规部分因析设计,其试验次数小于等于各因子主效应个数.在试验成本十分昂贵时使用超饱和设计能有效减少试验次数,节约试验成本,因而对超饱和设计的研究一直是实践和理论研究的热点问题之一.Booth和Cox[39]提出了用E(s2)来评价二水平超饱和设计的优劣,希望超饱和设计d的E(s2)越小越好,即希望因子之间的平方相关系数的平均最小化,这就是著名的E(s2)准则.Zhang和Qin[23]指出这一准则可以用基于均匀性模式UP(d;1)的MPU准则来替代,因为这一准则与MPU准则之间具有如下关系: 定理6 假定设计d∈(n;2s),且是强度为1的正交设计,则 对于混水平超饱和设计,Yamada和Matsui[40]提出了一个χ2统计量来度量两因子间的非正交性,Liu,Fang和Hickernell[19]将其推广到可以度量任意t(t≥2)个因子间的非正交性,并发现χ2统计量与均匀性模式之间有下列关系: 定理7 设计d∈(n;q1×…×qs),且是强度为t(t≥2)的正交设计,则 注意到Tang[36]提出的V-准则类似于最小χ2准则,因此定理7可看作是定理5从二水平到混水平情形的推广. 均匀性模式的准确下界可以用来评价一个给定的试验设计的均匀性程度,若给定的试验设计的均匀性模式越接近下界,那么该设计的均匀性程度就越高.若一个设计的均匀性模式达到其下界,则根据定义2可知该设计即为MPU设计.同时,均匀性模式的下界可以用来作为寻找、构造均匀设计的基准,特别是在随机优化算法中,若某步迭代步骤达到这个下界,则算法就可以终止.已有一些文献致力于探索均匀性模式的下界,其中基于均匀性模式UP(d;1),Zhang和Qin[23]及Qin和Chatterjee[28]分别针对二水平设计和一类特殊的混水平设计给出了不同的下界. 定理8对设计d∈(n;2s),1≤i≤s,有 其中,Rn,i与n关于2i同余.特别地,若d还是U型设计时,则D(1)(d;1)=0, 上述定理中设计d任意两行的相遇数是指这两行中对应位置元素相等的分量个数. 定理9 假定设计d∈(n;p×2s),第一个因子水平为p,且各水平出现次数相同,则 当p=2r+1时, 基于均匀性模式UP(d;2),Qin,Wang和Chatterjee[27]利用Kronecker积的性质得到了下列结果: 定理10对任意设计d∈(n;qs),定义则对1≤g≤s,有 基于均匀性模式UP(d;3),Qin,Wang和Chatterjee[29]针对二三混水平设计也得到了下列结果: 定理11对任意设计d∈(n;2s1×3s2),定义γj1j2=).则对1≤g≤s,有 其中,g2=g-g1. 基于均匀性模式UP(d;4),对一般混水平设计,汪政红[30]得到了下列结论: 定理12 任给设计d∈(n;q1×…×qs),和任意二元向量x=(x1,x2,…,xs),xi=0或1,定义令|xi=0或则对1≤g≤s,有 D(i)(d;)+低阶项,其中,“低阶项”是指j 称这一规则为最小低阶投影均匀性规则(MPU规则). 例1表1中的设计d1,d2分别达到了定理9中相应的下界,因此分别是设计类(16;4×23)与(20;5×23)中基于中心化L2偏差的MPU设计. 表1 基于中心化L2偏差的MPU设计 例2表2中的3个等水平设计均达到了定理10中相应的下界,因此分别是设计类(27;34),(8;44),(7;73)中基于离散偏差I的MPU设计,其中d3还是34-1最小低阶混杂设计(见文献[43]). 表2 基于离散偏差I的MPU设计 例3 表3中给出的两个混水平设计均达到了定理12中相应的下界,因此分别是设计类(12;6×4×3×2)及(12;3×44)中基于离散偏差II的MPU设计. 例4 表4给出的二三混水平设计d8,其基于中心化L2偏差的均匀性模式达到了定理9中给出的下界,因此是设计类(48;25×31)中基于中心化L2偏差的MPU设计,同时,其基于Lee偏差的均匀性模式也达到了定理11中给出的下界,因此还是设计类(48;25×31)中基于Lee偏差的MPU设计,基于离散偏差II的均匀性模式也达到了定理12中给出的下界,因此也是设计类(48;25×31)中基于离散偏差II的MPU设计. 表3 基于离散偏差II的MPU设计 表4 设计d8∈(48;25×31) Tab.4 design d8∈(48;25×31) 表4 设计d8∈(48;25×31) 转置后的设计矩阵1111111100000000 0000000011111111 1111111000000001111000011110000 0000111100001111 11110000111100001100110011001100 0011001100110011 11001100110011001010101010101010 0101010101010101 10101010101010101001011001101001 0110100110010110 10010110011010010000000000000000 1111111111111111 2222222222222222UP(d8;1)(0,0,0,0,3 391,2 261)×10-6UP(d8;3)(0,0,0,0,1 8051,1 8054)×10-4UP(d8;4)(0,0,0,0,0 0035,0 0174) 本文对关于均匀性模式的研究文献进行了总结,给出均匀性模式以及基于它的最小低阶投影均匀性准则的统一定义,并对MPU准则的统计性质及其在补设计方面的应用等进行了归纳.均匀性模式与广义字长型、强度、B向量等之间的联系表明最小低阶投影均匀性准则与广义最小低阶混杂准则、正交性、V准则、最近平衡性准则、设计效率准则等是相互等价的,彼此之间可以互相支持,因而揭示了均匀设计和因子设计之间的内在关系.第5节的实例表明本文给出的这些均匀性模式的下界都是可以达到的,同时也说明了最小低阶投影均匀设计是存在的. 利用本文第3节中的下界,结合第2节中给出的均匀性模式与广义字长型,E(s2)、χ2等之间的解析关系,可以得到许多关于广义字长型、E(s2)等有用下界,有一些下界在参考文献中已经提及,此文就不再累述.最小低阶投影均匀性准则与V准则、最近平衡性准则、最小E(s2)准则等的联系主要还局限于二水平情形,关于更高水平的对称情形及各种混水平情形均有待进一步深入研究. 试验设计中补设计及折叠反转设计理论由于其实用性一直备受关注,本文总结了对称情形均匀性模式在补设计中的应用,而关于混水平情形目前还没有文献涉及.此外,现有文献已讨论了偏差准则在折叠反转设计中的应用,但用均匀性模式来研究最优折叠反转设计的文献还未见报道,均匀性模式以向量的形式衡量均匀性,比偏差更全面,因而以均匀性模式替代偏差作为均匀性的度量,探讨其在折叠反转设计等方面的应用是具有创新性和实践意义的课题. 随着科学技术的发展,试验涉及的因子个数越来越多,且每个因子的水平也各异,因而继续深入研究混水平均匀性模式的统计合理性、构造理论及其在补设计、折叠反转设计中的应用等问题,不仅会进一步丰富、完善均匀设计的理论和方法,而且还可以为均匀设计的实际应用提供新的理论依据和新的数据分析方法,满足科技工作者解决实际具体问题的需求. [1] 方开泰. 均匀设计:数论方法在试设计中的应用[J].应用数学学报, 1980, 3(4):363-372. [2] FangK T,Wang Y. Number-theoretic Methods in Statistics[M].London:Chapman and Hall,1994. [3] Weyl H. Math über die gleichverteilung der zahlem mod eins[J].Math Ann, 1916, 77:313-352. [4] Hua L K,Wang Y. Applications of number theory to numerical analysis[M].Berlin and Beijing:Springer and Science Press,1981. [5] Niederreiter H. Random number generation and quasi-Monte Carlo methods[C].SIAM CBMS-NSF Regional Conference Series in Applied Mathematics,Philadelphia,1992. [6] Hickernell F J. A generalized discrepancy and quadrature error bound[J].Ann Math Comp, 1998, 67:299-332. [7] Hickernell F J. Lattice Rules: How Well Do They Measure Up[C]//Hellekalek P,Larcher G.Random and Quasi-Random Point Sets Lecture Notes in Statistics, 1998, 138:109-166. [8] Zhou Y D, Ning J H, Song X B. Lee discrepancy and its applications in experimental designs[J].Statist & Probab Lett, 2008, 78:1933-1942. [9] Chatterjee K, Qin H. Generalized discrete discrepancy and its applications in experimental designs[J].J Statist Planning and Inference, 2011, 141(2):951-960. [10] Fang K T, Li R Z, Sudjianto A. Design and Modeling for Computer Experiments[M].Boca Raton,FL:Chapman & Hall/CRC Press, 2006. [11] 方开泰, 刘民千, 周永道. 试验设计与建模[M].北京:高等教育出版社, 2011. [12] Hickernell F J, Liu M Q. Uniform designs limit aliasing[J].Biometrika, 2002, 89:893-904. [13] Qin H, Fang K T. Discrete discrepancy in factorial designs[J].Metrika, 2004, 60:59-72. [14] Qin H, Ai M Y. A note on connection between uniformity and genealized minimum aberration[J].Statistical Paper, 2007, 48:491-502. [15] Fang K T, Mukerjee R. A connection between uniformity and aberration in regular fractions of two-level factorial[J].Biometrika, 2000, 87(1):193-198. [16] Fang K T, Ma C X,Mukerjee R. Uniformity in fractional factorial[C]//Fang K T,Hickernell F J,Niederreiter H (eds) Monte Carlo and Quasi-Monte Carlo Methods 2000.Springer,Berlin, 2002:232-241. [17] Ai M Y, Li P F, Zhang R C. Optimal criteria and equivalence for nonregular fractional factorial designs[J].Metrika, 2005, 62:73-83. [18] Fang K T, Qin H. Uniformity pattern and related criteria for two-level fractionals[J].Science in China Ser A, 2005, 48:1-11. [19] Liu M Q, Fang K T, Hickernell F J. Connections among different criteria for asymmetrical fractional factorial designs[J].Statistica Sinica, 2006, 16: 1285-1297. [20] Qin H, Zou N, Chatterjee K. Connection between uniformity and minimum moment aberration[J].Metrika, 2009, 70:79-88. [21] Box G E P, Meyer R D. An analysis for unreplicated fractional factorials[J].Technometrics, 1986, 28(1):11-18. [22] Xu H, Wu C F J. Generalized minimum aberration for asymmetrical fractional factorial designs[J].Ann Statist, 2001, 29(2):549-560. [23] Zhang S L, Qin H. Minimum projection uniformity criterion and its application[J].Statist.& Probab Lett, 2006, 76:634-640. [24] Song S, Qin H. Application of minimum projection uniformity criterion in complementary designs[J].Acta Mathematica Scientia, 2010, B30(1):180-186. [25] Qin H, Zou N, Zhang S L. Design efficiency for minimum projection uniformity designs with two levels[J].Journal of Systems Science and Complexity, 2011, 24(4):761-768. [26] Zhang A J, Fang K T, Li R Z,et al. Majorization framework for balanced lattice designs[J].Ann Statist, 2005, 33:2837-2853. [27] Qin H, Wang Z H, Chatterjee K. Uniformity pattern and related criteria for q-level factorials[J].J Statist Planning and Inference, 2012, 142:1170-1177. [28] Qin H, Chatterjee K. Lower bounds for the uniformity pattern of asymmetric fractional factorials[J].Communications in Statistics-Theory and Methods, 2009, 38:1383-1392. [29] Qin H,Wang Z H,Chatterjee K. Uniformity pattern of asymmetric fractional factorials[J]. Journal of Systems Science and Complexity,2015, 28:1-12. [30] 汪政红.均匀性模式及相关准则的研究[D].武汉:华中师范大学:2013. [31] Fries A, Hunter W G. Minimum aberration 2k-pdesigns[J].Technometrics, 1980, 22:601-608. [32] Ma C X, Fang K T. A note on generalized aberration factorial designs[J].Metrika, 2001, 53:85-89. [33] Tang B, Deng L Y. MinimumG2-aberration for nonregular fractional designs[J]. Ann Statist, 1999, 27(6):1914-1926. [34] Mandal A, Mukerjee R. Design efficiency under model uncertainty for nonregular fractions of general factorials[J].Statistica Sinica, 2005, 15:697-707. [35] Cheng C S, Deng L Y,Tang B. Generalized minimum aberration and design efficiency for non-regular fractional factorial designs[J].Statist Sinica, 2002, 12: 991-1000. [36] Tang B. Theory of J-characteristics for fractional factorial designs and projection justification of minimumG2-aberration[J].Biometrika, 2001, 88:401-407. [37] Fang K T, Lu X, Winker P. Lower bounds for centered and wrap-aroundL2-discrepancies and construction of uniform designs by threshold accepting[J].J Complexity, 2003, 19:692-711. [38] Qin H, Chen Y B. Some results on generalized minimum aberration for symmetrical fractional factorial designs[J].Statist Probab Lett, 2004, 66:51-57. [39] Booth K H V, Cox D R. Some systematic supersaturated designs [J].Technometrics, 1962, 4:489-495. [40] Yamad S, Matsui T. Optimality of mixed-level supersaturated designs[J].J Statist Plann Inference, 2002, 104:459-468. [41] Qin H. Characterization of generalized aberration of some designs in terms of their complementary designs [J].J Statist Plann Inference, 2003, 117:141-151. [42] Qin H, Wang Z H. Application of minimum projection uniformity criterion in complementary designs for q-level factorials[J].Front Math China, 2015, 10(2):339-350. [43] Xu H. Minimum moment aberration for nonregular designs and supersaturated designs[J].Statist Sinica, 2003, 13:691-708. Uniformity pattern and its applications in experimental designs QIN Hong1, WANG Zhenghong2,1 (1.School of Mathematics and Statistics, Central China Normal University, Wuhan 430079;2.School of Mathematics and Statistics, South-Central University for Nationalities, Wuhan 430074) Uniformity is known as a geometrical concept usually measured by various kinds of discrepancies.But discrepancies put particular emphasis on totality, namely consideration on the whole uniformity of all sub designs. According to the principle of effect hierarchy, lower dimensional projection uniformity is more important than higher dimensional ones. So many scholars proposed a new concept of uniformity pattern like word length pattern to measure the projection uniformity on different dimensions. This article presents a thorough review on existing relative literature and gives an unified definition for uniformity pattern and the criterion of minimum projection uniformity based on it. The application of MPU criterion on complementary designs and the connections between it as well as many other kinds of optimality criteria are summarized. These connections demonstrates that the MPU criterion is equivalent with criteria of generalized minimum aberration,orthogonality,V, nearest balance, design effciency,E(s2) and etc. In other words, they are supportive for each other, which indicates the internal relationship between uniform designs and factorial designs. Moreover, the lower bounds of uniformity pattern in existing literature and some illustrative examples of minimum projection uniform designs are concluded for convenience. uniformity pattern; minimum projection uniformity; generalized minimum aberration; orthogonality; complementary designs; lower bound 2015-05-08. 国家自然科学基金项目(11271147,11401596). 覃红(1966- ),男,教授,博士生导师,主要从事试验设计,多元分析,生物统计方面的研究. *通讯联系人. E-mail: wzh@mail.scuec.edu.cn. 1000-1190(2015)05-0647-10 O212.6 A2 MPU准则的统计合理性
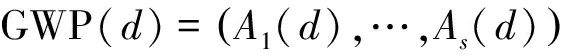



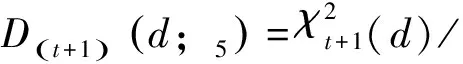
3 均匀性模式的下界

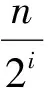
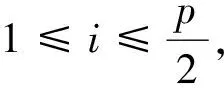
4 MPU准则在补设计中的应用




5 一些MPU设计的实例




6 小结
