刘华汉，蒋 玮，杨光辉，吕海霆

（大连理工大学 机械工程学院，辽宁 大连 116024）

0 引 言

机械产品的可靠性设计不同于电子产品可靠性设计.对机械系统来说有3种不同形式的相关性问题：一是考虑引起零件单模失效的随机变量相关性问题，二是考虑零件失效模式之间相关性问题，三是机械系统零件间的相关性问题.而对于机械系统中单个零件的可靠度分析，应充分考虑上述前两种相关性问题.目前的研究工作集中在零件失效模式间相关性问题及机械零件（单模失效）间的相关性问题［1－10］的研究方面，而对于机械零件随机变量相关的单模失效问题的研究鲜有报道.

机械零件可靠度计算的基本理论为应力－强度干涉理论（又称为应力－强度相干模型），在以往的文献中，此理论都是在应力和强度完全独立的情况下导出的，但实际上并不是所有的零件可靠性问题中的应力和强度完全独立，例如轴系零件设计变量的荷载、强度等因素之间存在程度不同的相关性［11］.同时，在需要考虑构件的自重时，构件的应力和强度之间也存在相关性［12］.喻天翔等［13］通过非线性变换，建立了仅考虑应力、强度两个随机变量相关时的零件单模失效可靠度模型，并探讨了相关系数对零件单模可靠度的影响及相对误差，但假设随机变量的分布都为正态分布且只考虑应力、强度两个变量相关.

引起机械零件广义应力与强度随机性的因素主要有材料、加工、制造、安装、荷载等，如同种材料性能分布的不均匀、制造精度误差.正是由于这些参数的随机性才有了可靠度的概念.要想得到这些因素的实际随机性参数是比较困难的，因此在理论分析中常常假设这些因素服从常见的分布，如正态分布、威布尔分布、指数分布等.现有的大多数文献中假设随机参数服从正态分布，但很多情况下并非如此.这时就需要探求随机变量因素服从其他分布时的可靠度计算公式，探求将非正态分布转化为正态分布的方法，利用正态分布运算的成熟的计算技术来求得零件可靠度.

本文针对引起机械零件单模失效的随机变量为不相关正态随机变量、相关正态随机变量、不相关非正态随机变量、相关非正态随机变量4种情况，借鉴结构可靠性求解理论，寻求建立机械零件单模失效可靠度求解模型的统一方法.主要是建立相关非正态随机变量的可靠度求解理论模型.不相关正态随机变量的可靠度理论是求解其他3种情况的基础.最后，通过齿轮传动的实例说明本文所提方法的有效性.

1 零件单模失效可靠度求解统一模型建立

全面考虑引起机械零件单模失效的各个因素：随机变量是否服从正态分布，随机变量之间是否具有相关性，随机变量之间是否为线性关系.机械零件单模失效可靠度求解统一模型框图如图1所示.设零件单模失效的极限状态方程为M＝G（X），其中X＝（X1X2…Xn）T为随机变量，它们共同影响失效状态函数中的应力强度.这些随机变量中可能含有非正态随机变量，各个随机变量之间可能存在相关性.下面将对统一模型由简单到复杂展开说明.

图1 机械零件单模失效可靠度模型Fig.1 Single failure mode reliability model of the mechanical components

1.1 随机变量正态分布不相关时零件单模可靠度求解理论

此为求解零件可靠度最简单也是基础的模型，如图1中Ⅰ框所示，计算步骤如下：

步骤1 正态随机变量正则化为标准正态随机变量.

假设影响极限状态方程的随机变量为Y＝（Y1Y2…Yn）T，极限状态方程为

其中Yi～N（μi，σ2i），各随机变量不相关，通过式（2）正则化为标准正态随机变量Z＝（Z1Z2…Zn）T，则极限状态方程转化为式（3）的形式：

步骤2 零件单模可靠度的求解.

将极限状态方程（1）以正则化后的标准正态随机变量表示为式（3），则式（3）分为两种情况：随机变量Zi的线性组合或非线性组合，下面分别表述：

（1）若极限状态方程（3）为n维标准正态随机变量Zi的线性组合：

可靠度指数

可靠度

（2）若极限状态方程（3）为非线性组合，则可采用两种方法求解.

①一 次 二 阶 矩（first－order second－moment，FOSM）法［17］.

将式（3）在平均值处一阶泰勒展开，仅保留一阶项：

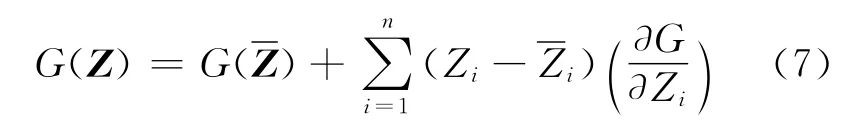
则

零件单模可靠度可由式（5）、（6）求得.

②改进的一次二阶矩（advanced first－order second－moment，AFOSM）法［18］.

通过求解式（9）得到可靠度指数β，代入式（6）求得可靠度.对于式（9）的求解可以采用Lagrange乘子迭代法导出的公式进行迭代计算，将在2.1中详细介绍.

1.2 随机变量正态分布相关时零件单模可靠度求解理论

假设影响极限状态方程的随机变量为X＊＝（X＊1X＊2…X＊n）T，极限状态方程为

步骤1 正态随机变量正则化为标准正态随机变量.

按照式（2）、（3）的形式将相关的非标准正态随机变量X＊＝（X＊1X＊2…X＊n）T正则化为相关的标准正态随机变量Y＊＝（Y＊1Y＊2…Y＊n）T，然后根据下述步骤2、步骤3进行零件单模可靠度的求解.

步骤2 相关的标准正态随机变量转化为不相关的正态随机变量.

将相关的标准正态随机变量Y＊＝（Y＊1Y＊2…Y＊n）T线性变换为不相关的正态随机变量Y＝（Y1Y2…Yn）T，Yi～N（μi，σi2）.

变换过程如下：

设随机变量Y＊＝（Y＊1Y＊2…Y＊n）T的协方差矩阵为

由线性代数理论可知，矩阵CY＊ 可通过式（12）线性变换成对角矩阵：

其中A是一个正交矩阵，它的列向量等于矩阵CY＊ 的特征向量，对角矩阵CY由式（13）计算：

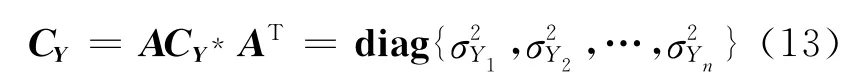
对角矩阵CY的对角元素σ2Yi等于矩阵CY＊ 的第i个特征值.由式（12）可得互不相关的正态随机变量Y＝（Y1Y2…Yn）T.

步骤3 变量正态分布相关时零件单模可靠度求解.

经过步骤1、步骤2所述方法变换后，可靠度的求解转化为1.1中讨论的问题，按照1.1中提供的方法就可以得到考虑随机变量正态分布且相关时的零件单模失效下的可靠度.

1.3 含有非正态随机变量且相关时零件单模可靠度求解理论

研究发现，自然界中大多数的物理量在经过无数次的统计分析后都近似服从正态分布，因此有关正态分布函数的性质、特征、数字特征等研究也最多，发展了许多可用的结论及大量的可供参考查阅的数据.基于此现行对于由高维极限状态函数表示的可靠度关系式的求解都是以各随机变量服从正态分布为前提下得出的.然而面对多维极限状态函数中含有非正态随机变量的情形，只有将非正态随机变量转化为正态随机变量，才能利用现有成熟的、计算精度高的可靠度理论进行机械零件可靠度的求解，本节将对随机变量中含有非正态随机变量的情形进行研究.

假设机械零件单模失效的极限状态方程为

其中X＝（X1X2…Xn）T，为影响应力、强度分布的随机变量，X中含有非正态随机变量且各随机变量之间具有相关性.此种情况下机械零件单模失效可靠度求解步骤如下：

步骤1 将X中的非正态随机变量转化为正态随机变量.

（1）Rosenblatt变换（Rosenblatt transformation，RT）［14］

Rosenblatt证明：任意非正态随机变量X，理论上都可以通过Rosenblatt变换转化为线性无关的标准正态随机变量Z.但这种变换具有局限性，需要知道n维随机变量X的联合累积分布函数，具体变换形式如下：

设n维随机变量X的联合累积分布函数为FX（X），则n维标准正态线性无关随机变量Z可以通过式（15）得到：

按顺序反求式（15）中的方程，可以得到n维标准正态线性无关随机变量Z：

式（16）中的条件概率密度函数通过联合概率密度函数按式（17）、（18）求得：

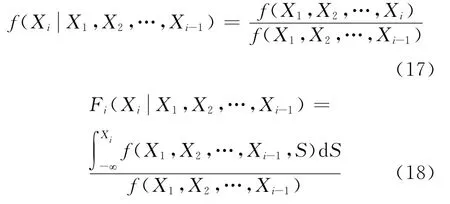
同理可通过逆变换按顺序反求式（16）得到X＝（X1X2…Xn）T.由式（16）变换求得不相关标准正态随机变量Z＝（Z1Z2…Zn）T.

（2）R－F变换［15］

设Xi为临界破坏面上的特定点，通过令原始分布FXi（Xi）和当量正态分布在特定点Xi处具有相等的概率密度函数和累积分布函数，则可求得当量正态分布的均值和标准差

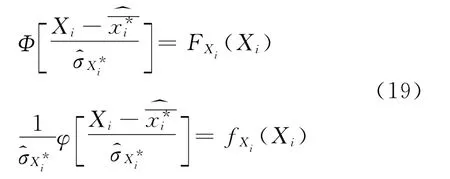
由式（19）得

变换得到正态随机变量X＊＝ （X＊1X＊2…X＊n）T.

步骤2 含有非正态随机变量且相关时零件单模可靠度求解.

利用Rosenblatt变换方法进行非正态随机变量的正态化时，必须利用随机变量的联合概率密度函数，这一点在实际中较难实现；但经过此种变换后，含有非正态随机变量且相关的随机变量经转换后直接转化为不相关的标准正态随机变量，此时利用1.1中所述的方法就可以快速地求出其可靠度.

R－F变换方法简单，较容易在计算机上实现，并不需要联合概率密度函数.将非正态随机变量正则化为标准正态随机变量Y＊＝ （Y＊1Y＊2…Y＊n）T；然后按照1.2中所述方法将相关正则化正态随机变量Y＊＝ （Y＊1Y＊2…Y＊n）T线性变换为不相关正态随机变量Y＝ （Y1Y2…Yn）T；最后按照1.1中所述方法求解得到考虑随机变量为非正态分布且相关时机械零件单模可靠度值.

2 机械零件单模失效可靠度求解算法

本章将根据第1章介绍的机械零件单模失效可靠度求解统一模型理论探讨可靠度求解的计算机实现算法，机械零件单模极限状态方程为式（14）描述的n维方程，含有非正态随机变量，且各随机变量之间存在相关性.算法中非正态随机变量利用R－F变换方法正则化为正态随机变量；可靠度指数β的求解采用H－L 方法，利用Lagrange乘子迭代法导出的公式进行迭代计算.

2.1 Lagrange乘子迭代法推导

Lagrange乘子迭代法详细叙述如下：

设

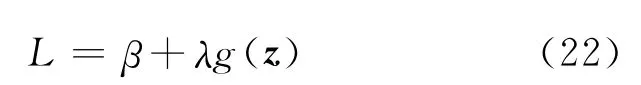
求L的极小值得

令

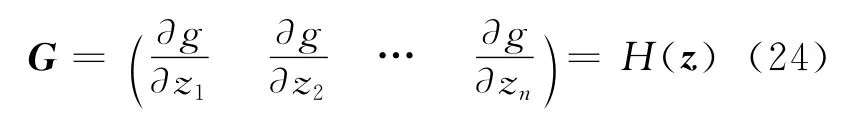
则式（23）可表示为

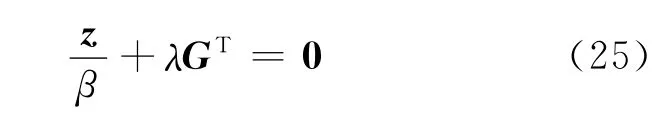
因此

所以

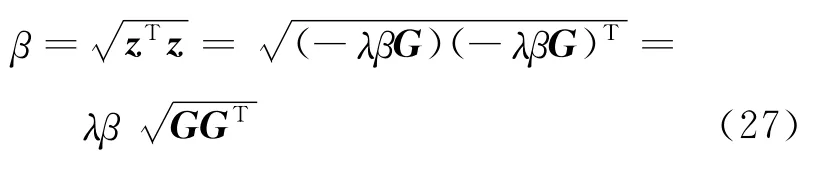
则

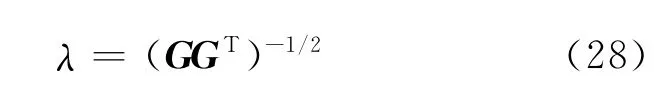
将式（28）代入式（26）得

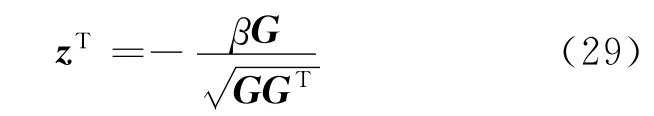
将式（29）代入式（21）得

采用数值方法可以计算出

则式（24）、（29）、（30）即可组成Lagrange乘子迭代法计算的迭代公式.

2.2 机械零件单模可靠度求解算法

假设影响零件单模可靠度的非正态随机变量为X＝（X1X2…Xn）T，由以上叙述得到可靠度求解算法的完整步骤如下：

步骤1 设置初始点x＝（x1x2…xn）T.

步骤2 在设计点x＝（x1x2…xn）T处利用式（19）、（20）进行R－F 变换，得到，将非正态随机变量在xi处转换为正态随机变量x＊i.

步骤4 对相关的标准正态随机变量y＊＝（y＊1y＊2…y＊n）T按照式（11）～（13）线性变换为互不相关的正态随机变量y＝ （y1y2…yn）T.

步骤5 将y＝（y1y2…yn）T由式（2）正则化为互不相关的标准正态随机变量z＝（z1z2…zn）T，形成临界破坏面g（z）＝0.

步骤6 在z处计算

步骤7 将zT＝βηα代入g（z）＝0并解得β＝β＋min.

步骤8 采用步骤7计算得到的β重新计算zT＝βηα.

重复步骤6～8直到计算结果收敛（以z稳定作为收敛指标）.

步骤12 由式（5）求得可靠度指数，式（6）求得机械零件单模失效可靠度.

3 算 例

本文以某1.6 MW 风力发电机平行级直齿圆柱齿轮传动为研究对象，通过对风机齿轮箱传动系统受力分析得到直齿圆柱齿轮传动各项参数：齿轮材料及热处理为17CrNiMo6低碳合金钢、渗碳淬火，小齿轮转矩T1＝2.542 8×107N·mm，小齿轮转速n1＝1 600r／min，齿数Z1＝19，Z2＝94，齿轮模数m＝12mm，齿宽系数φd＝0.4，重合度εa＝1.36，齿轮精度7 级，表面粗糙度Ra＝3.2，使用寿命为20a，高速、轻微振动.本文仅针对齿轮传动的齿面接触疲劳可靠性进行分析.

按国家标准规定的方法计算或查线图得到与齿面接触疲劳可靠性相关各参量的均值［19］和文献［20］中给出的方法估算原则得到各参量的均值和标准差如下：Ft＝（81 785.964 9，4 089.298 2）N，d1＝（228，1.14）mm，b＝（91.2，0.456）mm，KV＝（1.323，0.145 5），KHβ＝（1.348 4，0.044 5），KHα＝（1.225 4，0.040 4），ZV＝（0.949 2，0.031 3），KA＝（1.5，0.049 5），σHlim＝（1 450，174）MPa，ZN＝（1，0.033），ZL＝（1，0.033），ZR＝（2.783 6，0.091 9），ZW＝（1，0.005），ZX＝（0.958，0.004 8），ZH＝（2.494 6，0.012 473），ZE＝（189.8，0.949）定义极限状态方程为

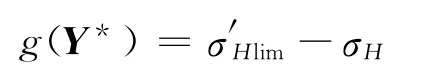
以上各参数的含义及应力σH、强度σ′Hlim的计算式参考国家标准GB 3480—1997.下面分3 种情况对该齿轮传动的可靠度进行求解.

（1）假设各随机变量均服从正态分布，其均值和方差如前所述，各随机变量之间相互独立，此种情况下根据文献［21］提供的方法计算得到可靠度指标β＝1.374 112，R＝0.915 330 5.

（2）假设各随机变量均服从正态分布，相关随机变量之间的相关性以齿面接触疲劳应力－强度干涉理论中应力σH与强度σ′Hlim之间的相关性代替，相关系数为ρ.由文献［21］方法得到该齿轮传动的齿面接触疲劳应力S为σH～N（2 887.905 4，205.214 62），齿面接触疲劳强度δ为σ′Hlim～N（3 670.270 5，531.088 12），则得到可靠度指标

当相关系数ρ在区间［－1，1］内变化，得到可靠度指数β、可靠度R随ρ变化曲线如图2所示.

图2 ρ－β、ρ－R 曲线Fig.2 ρ－β，ρ－Rcurves

由图2可知，在相关系数ρ从－1 增大到1（即应力、强度相互独立到应力、强度完全相关）时，可靠度指数β从1.063 1增大到2.400 8，相应的可靠度R从0.856 010增大到0.991 802，可靠度R的相对变化率为15.86%，变化较大.此时若忽略应力、强度之间的相关性将会产生两种结果：若实际为正相关，此时利用独立假设理论就会低估系统本身可靠性，通过改变设计来提高其可靠度时设计成本增高，造成不必要的浪费；若实际为负相关，则高估了系统的可靠性，按照此可靠性设计的产品，因过早的失效破坏而达不到设计要求.

以简单的应力、强度双变量相关的模型为基础，分析相关系数对不同零件单模可靠度的影响.以应力、强度相互独立时可靠度为基准，求解可靠度随相关系数在［0，1］内的变化曲线，通过对多种具有不同基准可靠度的机械零件ρ－R曲线分析知，基准可靠度越小，考虑与不考虑相关系数时的可靠度差别越大.因此可以得出结论，当在假设变量相互独立情况下求得的可靠度较大时（如0.999），变量之间的相关性可以忽略，以它们相互独立求得可靠度，这样不仅简化了计算，还不会影响机械零件可靠性优化设计的精度.

（3）假设各随机变量服从正态分布，通过分析国家标准GB 3480—1997 中各随机参数的计算知某些随机变量之间具有相关性：Ft、KV、KHα、KHβ、ZV、b与d1具有相关性；KHβ与b具有相关性.

定义可靠度极限状态方程中各随机变量为

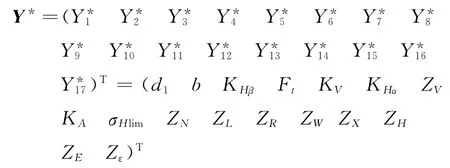
根据各随机变量计算式设定相关随机变量相关系数为

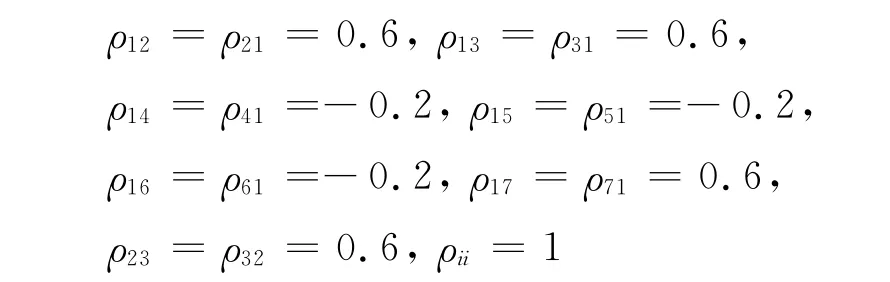
假设相关随机变量线性变换为非相关变量后的随机变量为z＝（z1z2…zn）T，利用本文介绍的求解算法求解此种情况下的可靠度，设初始值为z＝（1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1）T，以前后两次迭代z向量之间的距离作为收敛判据：经过3次迭代后可靠度指数β稳定在4.216 7，并且经过6次迭代后距离L达到7.637 1×10－5.所以求得的可靠度为R＝Φ（4.216 7）＝0.999 987 6.

（4）假设随机变量Ft、KV、KHα、KHβ、ZV、b、d1服从对数正态分布，7个变量间的相关性情况与（3）中所述相同；其他随机变量服从正态分布；所有随机变量的均值和标准差同上.利用本文介绍的求解算法，求解此种情况下的可靠度.外层经5次循环，内层循环分别为63、65、67、68、69次时，可靠度指数β稳定在4.202 1，此时精度为1×10－6.所以求得的可靠度为R＝Φ（4.202 1）＝0.999 987 2.

由以上讨论可知，本文介绍的变量相关的机械零件单模可靠度求解算法是可行的，且具有较高的收敛速度，对于复杂的变量相关的可靠度的求解具有重要的应用价值.另外，从考虑各个变量之间的相关性与将只考虑广义应力、强度之间单相关性求得的可靠度可以看出，差别很大，因此在求解变量相关可靠度时，为使求得的可靠度比较精确，应尽量将各个相关变量的相关性做单独处理，不要将其等效为应力、强度之间的相关性.

4 结 论

（1）本文以系统中机械零件的单模失效为研究对象，通过探讨影响单模失效极限状态方程的随机变量的不同特征：是否含有非正态随机变量、随机变量间是否相关，建立了考虑含有非正态随机变量和随机变量具有相关性时的机械零件单模失效下可靠度求解的统一模型，并对统一模型求解的理论进行了详细的论述.

（2）基于所建立的机械零件单模失效下的可靠度求解统一模型，提出了高效的计算机求解算法.

（3）通过算例说明了随机变量之间的相关性对零件单模失效可靠度的影响，表明在零件单模失效求解中忽略随机变量的相关性将会带来较大的误差.通过分析得到，当基准可靠度较大时（如0.999 9），变量之间的相关性可以忽略，这样在不影响优化设计精度的前提下简化了可靠度的计算.

（4）本文提出的理论为含有非正态随机变量时零件单模失效下可靠度的求解提供了一个很好的方法.实例证明，所提出的计算机实现算法收敛速度快，具有很强的实用性.

本文所建立的机械零件单模失效下可靠度求解模型可应用于机械零件任意一种失效模式下的可靠度求解，如热疲劳、磨损、温度失效等，这对机械零件考虑多模失效下可靠度理论的发展也具有指导作用.

［1］ Cornell C A.Bounds on the reliability of structural systems［J］.Journal of Structural Division，1967，93（1）：171－200.

［2］ Ditlevsen O.Narrow reliability bounds for structural systems ［J］.Journal of Structural Mechanics，1979，7（4）：453－472.

［3］ FENG Yuan－sheng.A method for computing structural system reliability with high accuracy［J］.Computers ＆Structures，1989，33（1）：1－5.

［4］ 董 聪.现代结构系统可靠性理论［D］.西安：西北工业大学，1993.DONG Cong.The reliability theory of modern structural system ［D］.Xi′an：Northwestern Polytechnical University，1993.（in Chinese）

［5］ 孙玉秋，张祖明.机械系统可靠度计算方法——阶段连续界限理论［J］.机械设计与制造，2001（2）：3－5.SUN Yu－qiu，ZHANG Zu－ming.Reliability calculation method of the mechanical system—phases sequence bounds theory ［J］.Machinery Design ＆ Manufacture，2001（2）：3－5.（in Chinese）

［6］ 喻天翔，孙玉秋，张祖明.多模式失效的机械零件可靠度计算新理论［J］.机械工程学报，2003，39（3）：134－138.YU Tian－xiang，SUN Yu－qiu，ZHANG Zu－ming.Reliability computing new theory of mechanical elements with multi failure mode ［J］.Chinese Journal of Mechanical Engineering，2003，39（3）：134－138.（in Chinese）

［7］ 王 正，谢里阳，李 兵.多种失效模式下的机械零件动态可靠性模型［J］.中国机械工程，2007，18（18）：2143－2146.WANG Zheng，XIE Li－yang，LI Bing.Timedependent reliability model of component with multiple failure modes ［J］.China Mechanical Engineering，2007，18 （18）：2143－2146.（in Chinese）

［8］ 王 正，谢里阳，李 兵.考虑载荷作用次数的失效相关系统可靠性模型［J］.东北大学学报：自然科学版，2007，28（5）：704－707.WANG Zheng，XIE Li－yang，LI Bing.Reliability model of failure－dependent system with frequency of loading taken into account ［J］.Journal of Northeastern University：Natural Science，2007，28（5）：704－707.（in Chinese）

［9］ Neves R A，Mohamed－Chateauneuf A，Venturini W S.Component and system reliability analysis of nonlinear reinforced concrete grids with multiple failure modes［J］.Structural Safety，2008，30（3）：183－199.

［10］ 闫 明，张义民，李 鹤，等.机械零件相关失效可靠度计算的二重积分模型［J］.东北大学学报：自然科学版，2011，32（10）：1460－1463.YAN Ming，ZHANG Yi－min，LI He，etal.Double integration model for reliability computation of mechanical components at dependent failure modes［J］.Journal of Northeastern University：Natural Science，2011，32（10）：1460－1463.（in Chinese）

［11］ 吴 波.轴的多失效模型与可靠性研究［J］.机械设计，1998，15（6）：47－48，57.WU Bo.Study on the multi－failure mode model and reliability of the shaft ［J］.Journal of Machine Design，1998，15（6）：47－48，57.（in Chinese）

［12］ 何水清，王 善.结构可靠性分析与设计［M］.北京：国防工业出版社，1993.HE Shui－qing，WANG Shan.Structure Reliability Analysis and Design［M］.Beijing：National Defense Industry Press，1993.（in Chinese）

［13］ 喻天翔，成刚虎，张选生，等.考虑变量相关的机械零件可靠度计算［J］.西安理工大学学报，2003，19（1）：73－75.YU Tian－xiang，CHENG Gang－hu，ZHANG Xuansheng，etal.Reliability computation of mechanical parts in considering variable correlations ［J］.Journal of Xi′an University of Technology，2003，19（1）：73－75.（in Chinese）

［14］ Rosenblatt M.Remarks on a multivariate transformation ［J］.Annals of Mathematical Statistics，1952，23（3）：470－472.

［15］ Rackwitz R，Fiessler B.Structural reliability under combined random load sequences ［J］.Computers and Structures，1978，9（5）：489－494.

［16］ Cramér H.Mathematical Methods of Statictics［M］.New Jersey：Princeton University Press，1999.

［17］ Cornell C A.Structural safety specifications based on second－moment reliability analysis［J］.IABSE Reports of the Working Commissions，1969，4：235－245.

［18］ Hasofer A M，Lind N C.Exact and invariant second－moment code format ［J］.Journal of Engineering Mechanical Division，ASCE，1974，100（EM1）：111－121.

［19］ 《现代机械传动手册》编辑委员会.现代机械传动手册［M］.2版.北京：机械工业出版社，2002.Editing Committee of Modern Handbook of Mechanical Transmission.Modern Handbook of Mechanical Transmission ［M］.2nd ed.Beijing：China Machine Press，2002.（in Chinese）

［20］ 张义民.汽车零部件可靠性设计［M］.北京：北京理工大学出版社，2000.ZHANG Yi－min.Reliability Design of the Auto Components ［M］.Beijing：Beijing Institute of Technology Press，2000.（in Chinese）

［21］ 芮延年，傅戈雁.现代可靠性设计［M］.北京：国防工业出版社，2007.RUI Yan－nian，FU Ge－yan.Modern Reliability Design ［M］.Beijing：National Defense Industry Press，2007.（in Chinese）