周　欣，　赵　彬

(陕西师范大学　数学与信息科学学院，　陕西　西安　710119)



格中粗糙集的若干性质

周欣，赵彬*

(陕西师范大学数学与信息科学学院，陕西西安710119)

摘要：利用粗糙集的理论方法,对格的粗糙集和S-模糊粗糙集的一些性质进行研究。证明了上近似算子在分配格的理想(滤子)之集上的不动点之集关于包含序构成一个凝聚的Frame,给出了下近似算子在有限格的理想(滤子)之集上不动点的刻画。最后,研究了格的S-模糊粗糙子格(理想、滤子)的一些性质。

关键词:粗糙集;S-模糊粗糙集;上(下)近似算子;理想;滤子;不动点

MRsubjectclassification:06B35

粗糙集理论是由Pawlak[1]首次提出的，旨在解决信息系统中的不确定性问题。事实证明,粗糙集理论在人工智能、数据分析和认知科学中非常重要。随着粗糙集理论的发展,许多学者开始考虑将粗糙集理论及其研究方法应用到多种代数结构的研究中[2-5]。Biswas和Nanda首次引入粗子群的概念后[6],Kuroki定义了半群的粗糙理想并关于半群的同余给出了上、下近似集的一些性质[7]。接着,Davvaz将粗糙集理论与环论结合起来,给出了关于一个环理想的粗糙理想和粗糙子环的概念[8]。另外,Davvaz等人又相继研究了模[9]、超结构[10]和MV-代数[11]上粗糙集的性质。文献[12-13]将粗糙集理论与格论联系起来,其中文献[12]给出了格的上、下粗糙理想(滤子)的定义并研究了它们的一些性质,文献[13]研究了格的粗糙模糊集。本文在文献[12]的基础上进一步研究格中粗糙集的性质,证明上近似算子在分配格的理想(滤子)集上的不动点之集关于包含序构成一个凝聚的Frame,并给出下近似算子在有限格的理想(滤子)之集上不动点的刻画。最后,本文结合文献[14]提出的模糊粗糙集的定义和文献[8]的研究方法,研究格的S-模糊粗糙集。

1预备知识

本节给出格论与粗糙集理论的一些基本概念与结论,未提及的概念和结论请参阅文献[15]。

设L是非空偏序集,若∀a、b∈L，a∨b与a∧b都存在,则称(L,≤)为格。设M是格L的非空子集,若a、b∈M⟹a∨b∈M且a∧b∈M,则称M是L的子格。

设θ是格L上的等价关系。如果θ与L的有限交和有限并相容，即∀(a,b)、(c,d)∈θ⟹(a∨c,b∨d)、(a∧c,b∧d)∈θ,则称θ是L上的同余关系。用[a]θ标记a的θ-同余类，用Con(L)标记格L上的同余之集。

定义1[12]设θ是格L上的同余。若∀a、b∈L,[a∨b]θ={x∨y:x∈[a]θ,y∈[b]θ},则称θ是∨-完备的。类似地，如果∀a、b∈L,[a∧b]θ={x∧y:x∈[a]θ,y∈[b]θ}，则称θ是∧-完备的。

命题1[1]设θ是非空集合X上的等价关系，则∀A、B⊆X，

(4)θ(A∩B)=θ(A)∩θ(B);

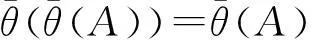
2上、下近似算子的不动点

本节在文献[12]的基础上进一步研究上、下近似算子在格的理想(滤子)集上的不动点集的性质。

命题2[12]设θ是格L上的同余,则下列结论成立:

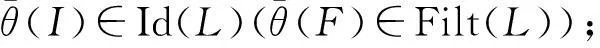
(2)设I和J是L的理想,则

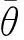
(4)设θ是L上的∧-完备同余,I⊆L且θ(I)≠∅。若I∈Id(L)，则θ(I)∈Id(L)。若I是L的素理想,则θ(I)是L的素理想。

命题3设I和J是L的子集,

(1)若θ(I)=I,则θ(I∩θ(J))=I∩θ(J);

(2)若F1、F2∈Filt(L)，则

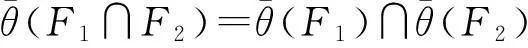
证明由命题1和2容易验证。

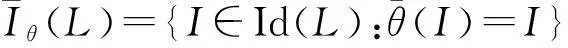
命题4Iθ(L)(Fθ(L))对Id(L)(Filt(L))的任意非空并封闭。

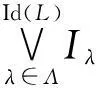
引理2在格L上,下列结论成立：

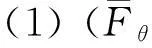
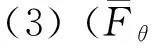
证明证明过程与文献[12]中引理3.17、命题3.18和3.20的证明类似。

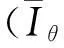
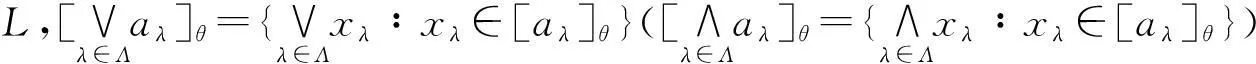
命题6设L有限格且θ是L上的同余，则下列结论成立：

(1)若θ是∨-完备同余，则

Iθ(L)={↓∨[x]θ:x∈L};

(2)若θ是∧-完备同余，则

Fθ(L)={↑∧[x]θ:x∈L}。

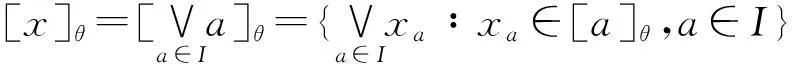
反过来，∀x∈L，显然有↓∨[x]θ∈Id(L)且θ(↓∨[x]θ)⊆↓∨[x]θ。∀a∈↓∨[x]θ,b∈[a]θ，因为(a,b)∈θ且a≤∨[x]θ，所以

(∨[x]θ,b∨(∨[x]θ))=

(a∨(∨[x]θ),b∨(∨[x]θ))∈θ，

从而b∨(∨[x]θ)∈[∨[x]θ]θ=[x]θ，因此∨[x]θ≤b∨(∨[x]θ)≤∨[x]θ，故b∨(∨[x]θ)=∨[x]θ。由此可得b≤∨[x]θ，即b∈↓∨[x]θ。由b的任意性知[a]θ⊆↓∨[x]θ，所以a∈θ(↓∨[x]θ)。又由a的任意性知↓∨[x]θ⊆θ(↓∨[x]θ)。因此，↓∨[x]θ=θ(↓∨[x]θ),即↓∨[x]θ∈Iθ(L)。由x的任意性知{↓∨[x]θ:x∈L}⊆Iθ(L)。因此，Iθ(L)={↓∨[x]θ:x∈L}。

上述命题说明，若L是有限格且θ是L上的∨-完备同余(∧-完备同余)，则下近似算子θ在Id(L)(Filt(L))上的不动点恰是↓∨[x]θ(↑∧[x]θ),x∈L。下面给出例子来说明命题6的逆命题一般不成立。

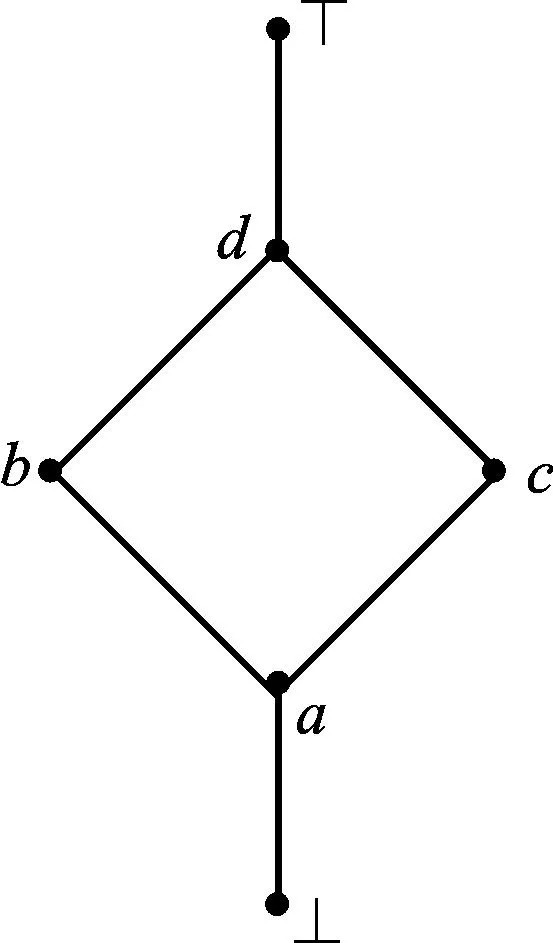
图1　L的哈塞图Fig.1　Hasse　graph　of　L

3S-模糊粗糙理想和S-模糊粗糙滤子

本节给出S-模糊粗糙子格和S-模糊粗糙理想(滤子)的概念并研究它们的相关性质。

由文献[13]知若L的模糊子集A满足∀x、y∈L，μA(x∧y)∧μA(x∨y)≥μA(x)∧μA(y),则称A是L的模糊子格。如果模糊子集A满足∀x、y∈L，μA(x∨y)=μA(x)∧μA(y)，则称A是L的模糊理想。如果模糊子集A满足∀x、y∈L,μA(x∧y)=μA(x)∧μA(y)，则称A是L的模糊滤子。容易验证模糊理想和模糊滤子一定是模糊子格。

Dubois和Prade在文献[16]中将粗糙集模糊化并给出了模糊粗糙集的定义,而Nanda和Majumdar在文献[14]中又引入并分析了另一种模糊粗糙集。为了区分这两种模糊粗糙集的概念,称文献[14]中提出的模糊粗糙集为S-模糊粗糙集,并在本节重点研究格上S-模糊粗糙集的性质。

回顾文献[14]引入的S-模糊粗糙集的概念。

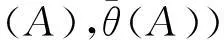
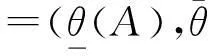
(2)θ(C)=θ(A)θ(B)当且仅当∀x∈θ(X),μθ(C)(x)=min{μθ(A)(x),μθ(B)(x)},且∀。

参考文献关于θ(A)=θ(B)和θ(A)θ(B)的定义可[14]。容易看出，θ(A)θ(B)和θ(A)θ(B)分别是S-模糊粗糙集θ(A)和θ(B)在粗糙集θ(X)的所有S-模糊粗糙集所组成集族中的下、上确界。

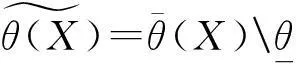
定义4[8]设D1=[a1,b1],D2=[a2,b2]是D([0,1])中的两个元素。定义max(D1,D2)=[a1∨a2,b1∨b2],min(D1,D2)=[a1∧a2,b1∧b2]。若a1≤a2且b1≤b2，则称D1≤D2。

下面给出S-模糊粗糙子格(理想、滤子)的定义。

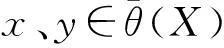
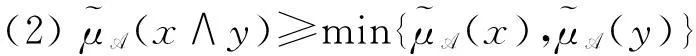
则称θ(A)是θ(X)上的一个S-模糊粗糙子格。

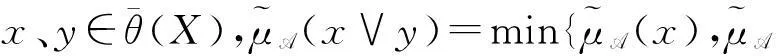
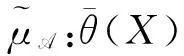
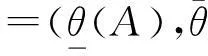
证明令θ(C)=θ(A)θ(B)，设x、y是中的任意两元素。因为是L的子格，所以。现证明(y)}。因为θ(A)和θ(B)是θ(X)的两个S-模糊粗糙子格，

所以

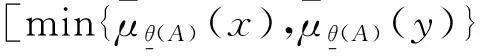
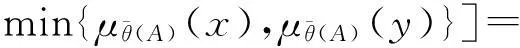
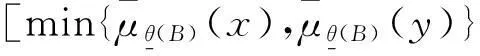
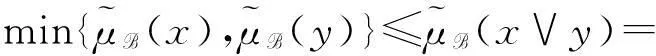
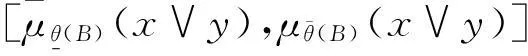
因此，

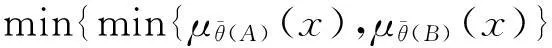
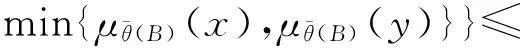
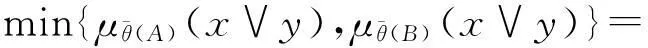
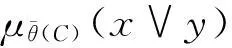
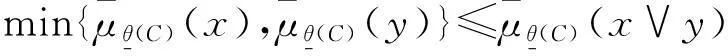
min{μθ(A)(x),μθ(A)(y)}≤μθ(A)(x∨y)且

min{μθ(B)(x),μθ(B)(y)}≤μθ(B)(x∨y)。

因此，

min{μθ(C)(x),μθ(C)(y)}=

min{min{μθ(A)(x),μθ(B)(x)},

min{μθ(A)(y),μθ(B)(y)}}=

min{min{μθ(A)(x),μθ(A)(y)},

min{μθ(B)(x),μθ(B)(y)}}≤

min{μθ(A)(x∨y),μθ(B)(x∨y)}=

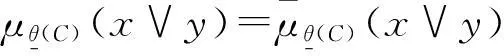
若x∉θ(X)或y∉θ(X),则

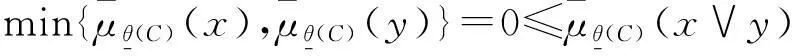
所以，

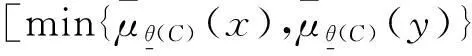
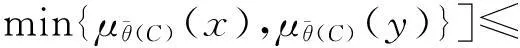
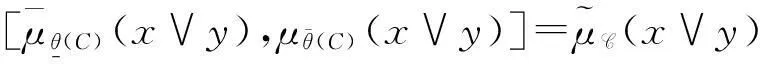
证明证明过程与命题7的证明类似。

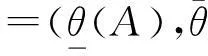
At={x∈θ(X):μθ(A)(x)≥t},

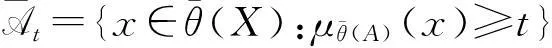
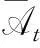
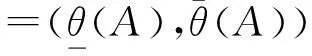
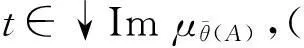
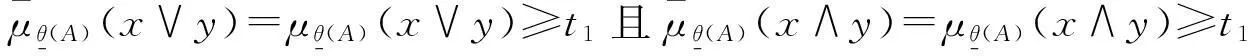
综上可知，

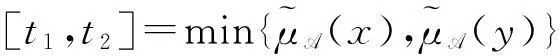
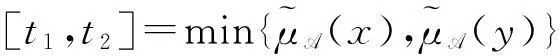
因此，θ(A)是θ(X)的S-模糊粗糙子格。

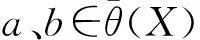
从而

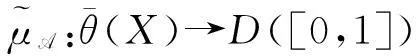
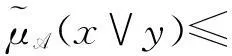
现在给命题10举一个例子。

例2设格L和L上的哈塞图如例1中所示。

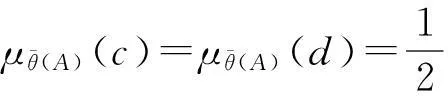
下面举例说明注1。

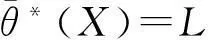
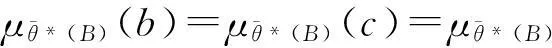
则θ*(B)是θ*(X)的S-模糊粗糙集，且

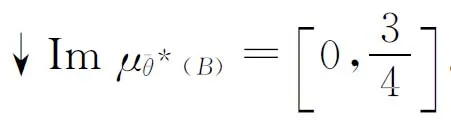
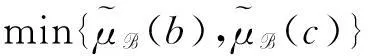
因此，θ*(B)不是θ*(X)的S-模糊粗糙子格。

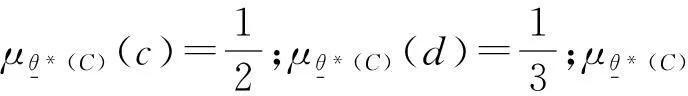
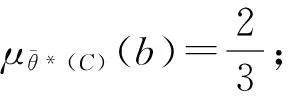
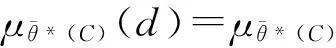
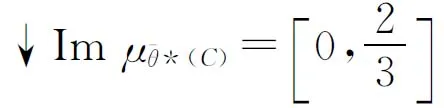
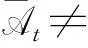
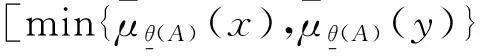
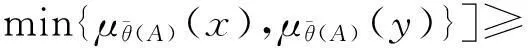
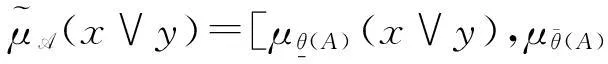
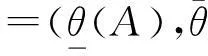
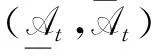
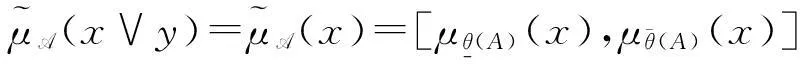
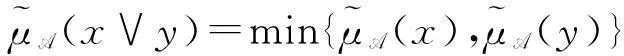
另一种情况可以类似地证明。

[1]PawlakZ.Roughsets[J].InternationalJournalofComputerandInformationSciences,1982,11:341-356.

[2]JunYB.RoughnessofΓ-subsemigroups/idealsinΓ-semigroups[J].BulletinoftheKoreanMathematicalSociety,2003,40(3):531-536.

[3]QiGL,LiuWR.RoughoperationsonBooleanalgebras[J].InformationSciences,2005,173:49-63.

[4]XiaoQM,ZhangZL.Roughprimeidealsandroughfuzzyprimeidealsinsemigroups[J].InformationSciences,2006,176:725-733.

[5]KazanciO,DavvazB.Onthestructureofroughprime(primary)idealsandroughfuzzyprime(primary)idealsincommutativerings[J].InformationSciences,2008,178:1343-1354.

[6]BiswasR,NandaS.Roughgroupsandroughsubgroups[J].BulletinofthePolishAcademyofSciencesMathematics,1994,42:251-254.

[7]KurokiN.Roughidealsinsemigroups[J].InformationSciences,1997,100:139-163.

[8]DavvazB.Roughnessinrings[J].InformationSciences,2004,164:147-163.

[9]DavvazB,MahdavipourM.Roughnessinmodules[J].InformationSciences,2006,176:3658-3674.

[10]DavvazB.Approximationsinhyperrings[J].JournalofMultiple-ValuedLogicandSoftComputing,2009,15:471-488.

[11]RasouliS,DavvazB.RoughnessinMV-algebras[J].InformationSciences,2010,180:737-747.

[12]EstajiAA,HooshmandaslMR,DavvazB.Roughsettheoryappliedtolatticetheory[J].InformationSciences,2012,200:108-122.

[13]EstajiAA,KhodaiiS,BahramiS.Onroughsetandfuzzysublattice[J].InformationSciences,2011,181:3981-3994.

[14]NandaS,MajumdarS.Fuzzyroughsets[J].FuzzySetsandSystems,1992,45:157-160.

[15]DaveyBA,PriestleyHA.Introductiontolatticesandorder[M].Cambridge:CambridgeUniversityPress,1990.

[16]DuboisD,PradeH.Roughfuzzysetsandfuzzyroughsets[J].InternationalJournalofGeneralSystems,1990,17(2/3):191-209.

〔责任编辑宋轶文〕

第一作者：李师，女，硕士研究生，研究方向为反应扩散方程理论及应用。E-mail:ashi2013@snnu.edu.cn

Somepropertiesofroughsetsinlattices

ZHOUXin,ZHAOBin*

(SchoolofMathematicsandInformationScience,ShaanxiNormalUniversity,

Xi′an710119,Shaanxi,China)

Abstract:RoughsettheoryisusedindiscussingsomepropertiesofroughsetsandS-fuzzyroughsetsinlattices.Itisprovedthatthesetofallfixedpointsunderanupperapproximationoperatoronthesetofallideals(filters)ofadistributivelatticeisacoherentframe.Acharacterizationforfixedpointsunderalowerapproximationoperatoronthesetofallideals(filters)ofafinitelatticeisgiven.FinallysomepropertiesofS-fuzzyroughsublattices(ideals,filters)ofalatticeareinvestigated.

Keywords:roughset;S-fuzzyroughset;upper(lower)approximationoperator;ideal;filter;fixedpoint

通信作者：*李艳玲，女，教授，博士。E-mail:yanlingl@snnu.edu.cn

基金项目：国家自然科学基金资助项目(11271236);教育部高等学校博士学科点专项科研 (100807180004)

收稿日期：2014-07-22

doi:10.15983/j.cnki.jsnu.2015.02.122

文章编号：1672-4291(2015)02-0008-07

中图分类号：O153.1

文献标志码：A