束方平，张毅，朱建青*

（1.苏州科技学院数理学院，江苏苏州215009，2.苏州科技学院土木工程学院，江苏苏州215011）

基于分数阶模型的Lagrange系统的积分因子与守恒量

束方平1，张毅2，朱建青1*

（1.苏州科技学院数理学院，江苏苏州215009，2.苏州科技学院土木工程学院，江苏苏州215011）

为了进一步研究基于分数阶模型的力学系统的守恒量，该文将积分因子方法应用于分数阶Lagrange系统，建立了寻找分数阶模型下Lagrange系统守恒量的一种新方法。首先，寻求分数阶Lagrange系统存在守恒量的必要条件和建立系统积分因子与守恒量的关系；其次，定义并给出用于确定积分因子的分数阶广义Killing方程；最后，得到基于分数阶模型的Lagrange系统的守恒量。文末举例说明结果的应用。

分数阶模型；Lagrange系统；积分因子；守恒量

自然界许多物理系统因其特殊的材料和化学特性而展现出分数阶动力学行为[1]，事实上，实际系统大多是分数阶的[2]，因此，利用分数阶模型来描述自然界和工程实际中的各种现象更为准确。分数阶微积分的研究扩展了人们的思路，填补了传统意义下微积分表示的缺陷。近年来分数阶微积分被广泛应用到各个领域，如物理学、金融学、水文学、高分子聚合物理、生物学、混沌动力学、控制理论等[3]。将分数阶微积分应用于力学系统建模问题要追溯到Riewe[4-5]的工作，他建立了力学系统的分数阶Euler-Lagrange方程和Hamilton正则方程。分数阶变分问题的对称性与守恒量的研究是分数阶动力系统的一个重要方面。Frederico和Torres基于变分原理引进分数阶守恒量的概念，首先研究了分数阶变分问题的不变性，给出分数阶Noether理论[6]。Atanackovi[7]等人研究了Riemann-Liouville分数阶导数定义下的不变性和Noether理论，并指出Frederico和Torres分数阶守恒量定义的不清晰性。

1 分数阶导数

左Remiann-Lionville分数阶导数的定义如下[15-16]右Remiann-Lionville分数阶导数的定义如下

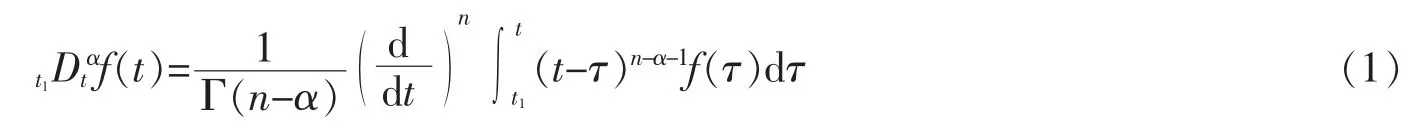
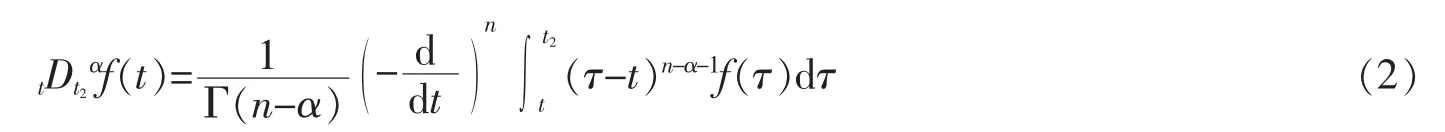
其中，f为区间[t1，t2]上的连续可微函数，Γ（*）为Gamma函数，n-1≤α＜n。若导数α为整数时这些导数就成为

Remiann-Lionville分数阶导数与整数阶导数的合成有如下关系

2 分数阶Lagrange系统及其积分因子

假设力学系统的位形由n个广义坐标qs（s=1，…，n）来确定。基于Remiann-Lionville分数阶导数，即Lagrange函数为[7]

分数阶Lagrange系统可表示为

定义1函数称为分数阶模型下Lagrange系统（7）的分数阶守恒量，当且仅当沿着运动方程（7）的解曲线恒成立

定义2如果不变式

恒等变为

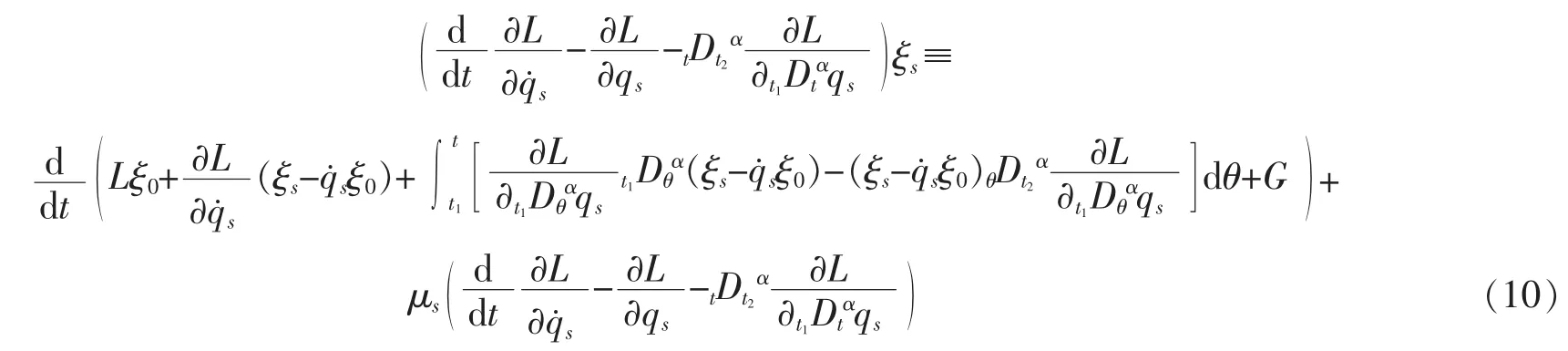
其中，ξ0，G和μs为的函数，则称为分数阶Lagrange系统（7）的积分因子。

3 守恒定理

联合式（7）和式（10），有

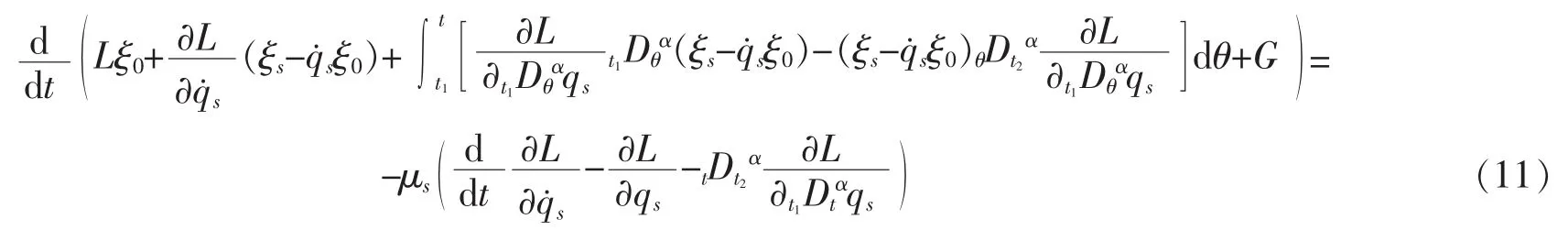
定理1如果函数ξs是分数阶Lagrange系统（7）的积分因子，那么系统存在守恒量（第一积分），形如

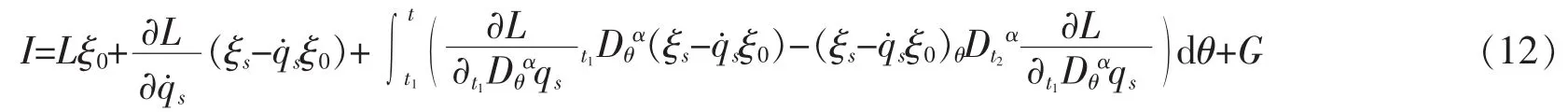
特别地，如果分数阶导数项消失，则可得到经典Lagrange系统的守恒量

对于Lagrange系统（7），如果函数ξs是其积分因子，那么每一组函数ξs，ξ0，G和μs一定满足必要条件（11），将方程（11）展开有

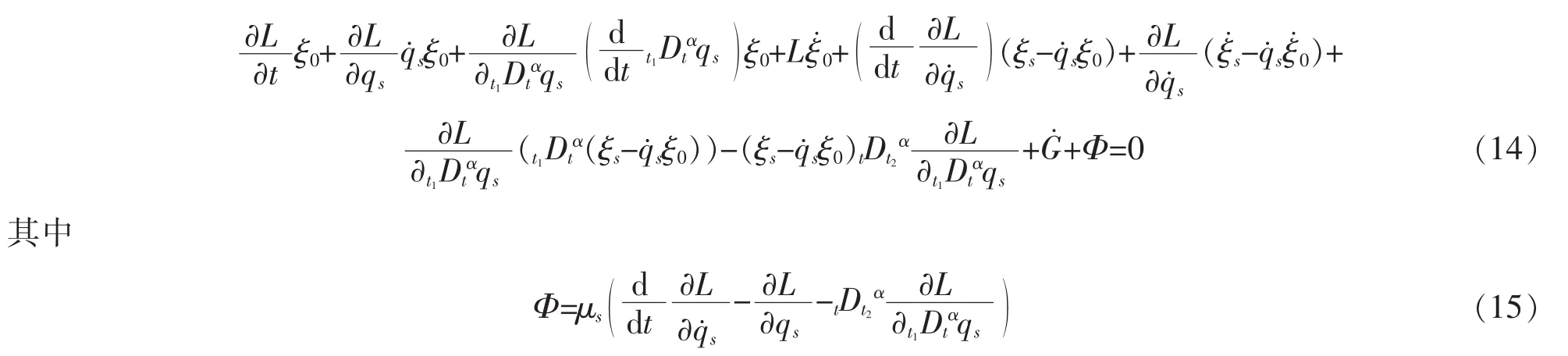
利用方程（7），式（14）可进一步写成

可见，如果函数组ξs，ξ0，G和μs满足必要条件（16），那么沿着Lagrange系统的运动轨线，该函数组使式（12）的右边成为一个常数。于是有

定理2如果函数组ξs，ξ0，G和μs满足必要条件（16），那么Lagrange系统（7）存在守恒量（12）。

积分方程（16）或利用其他方法可以求得函数组ξs，ξ0，G和μs对应于方程（16）的任意一个特解或函数解，由定理2可以得到Lagrange系统（7）的一个守恒量。

利用上述定理来寻求Lagrange系统的守恒量关键在于找到函数组ξs，ξ0，G，μs。由于函数ξs，ξ0，G不依赖于，将方程（16）展开，令含项的系数和不含项的系数分别为零，得到的线性偏微分方程为

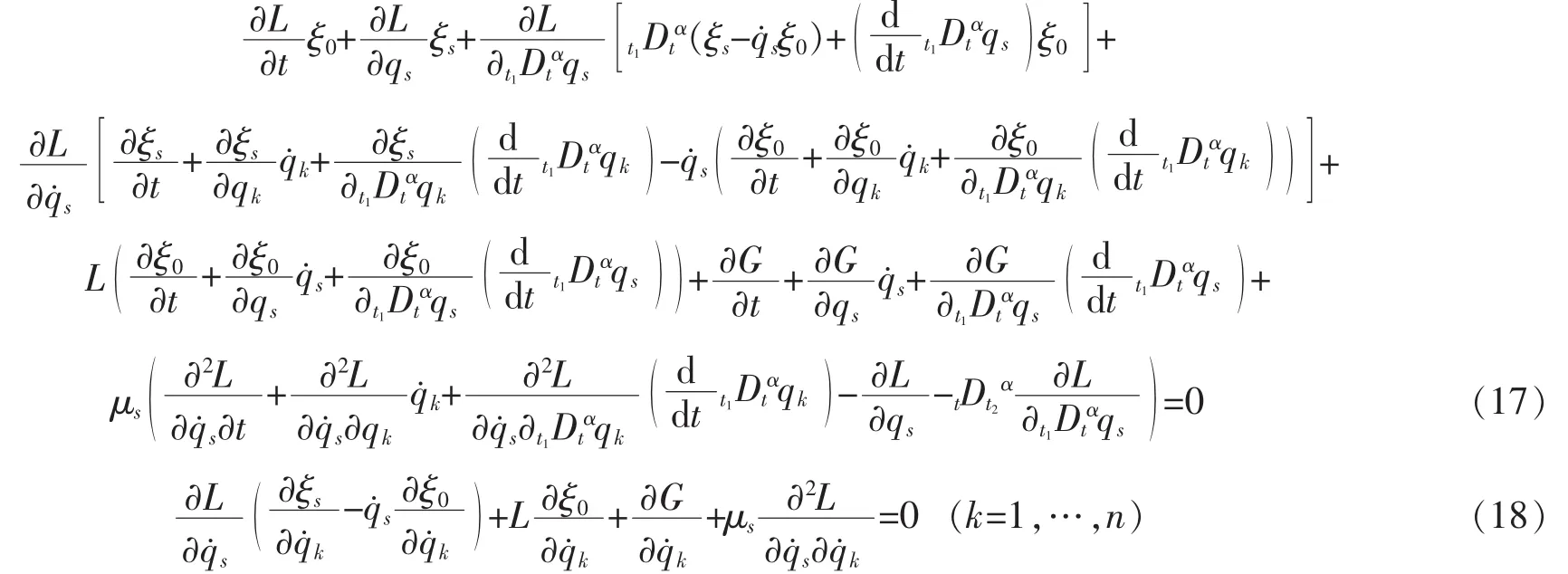
式（17）和（18）是关于（2n+2）个未知函数ξs，ξ0，G，μs的（n+1）个方程，称为广义Killing方程。由于方程数目小于未知函数的数目，故广义Killing方程的解不是唯一的，通过适当选取ξs，τ，G，μs可得到不同的守恒量。

4 算例

设力学系统的分数阶Lagrange函数

其中，ω为常数。

系统的运动微分方程为

广义Killing方程（17）、（18）给出

方程组（21）-（22）有解

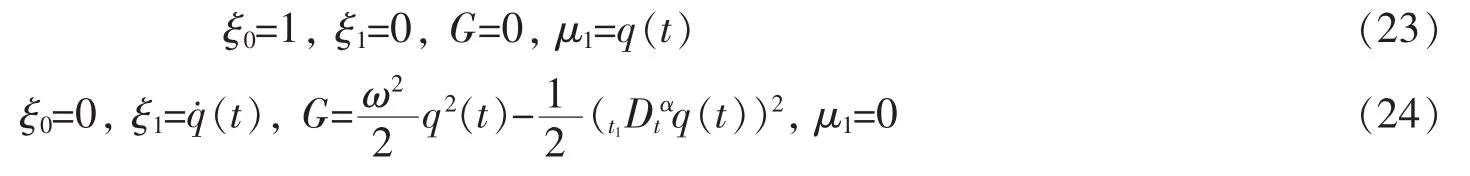
根据定理1和定理2，相应于函数组（23）-（24）系统存在如下守恒量

当α→1时，式（25）、（26）就成为

5 结语

寻求系统的守恒量是分数阶动力系统研究的一个重要方面。1984年，Djuki提出利用积分因子方法来构造完整非保守动力学系统的守恒量，该方法类似于构造保守系统能量积分的经典Lagrange方法，即通过运动微分方程乘以适当的积分因子的方法来直接构造系统的守恒量。该文是对积分因子方法应用的进一步研究，将积分因子方法应用于构造分数阶Lagrange系统的守恒量，提供了寻求分数阶Lagrange系统守恒量的一个新途径。

[1]朱呈祥，邹云.分数阶控制研究综述[J].控制与决策，2009，24（2）：161-169.

[2]Torvik P J，Bagley R L.On the appearance of the fractional derivative in the behavior of real material[J].Journal of Applied Mechanics，1984，51（2）：284-298.

[3]Kilbas A A，Srivastava H M，Trujillo J J.Theory and Applications of Fractional Differential Equations[M].Amsterdam：Elsevier B V，2006.

[4]Riewe F.Nonconservation Lagrangian and Hamiltonian mechanics[J].Physical Review E，1996，53（2）：1890-1899.

[5]Riewe F.Mechanics with fractional derivatives[J].Physical Review E，1997，55（3）：3581-3592.

[6]Frederico G S F，Torres D F M.A formulation of Noether’s theorem for fractional problems of the calculus of variations[J].Journal of Mathematical Analysis and Applications，2007，334：834-846.

[9]Qiao Y F，Zhang Y L，Han G C.Integrating factors and conservation therom for holonomic nonconservative dynamical system in generalized classical mechanics[J].Chinese Physics，2002，11（10）：988-992.

[10]乔永芬，张耀良，韩广才.非完整保守系统Raitzin正则运动方程的积分因子和守恒定理[J].兵工学报，2003，24（2）：162-166.

[11]Li R J，Qiao Y F，Liu Y.Integrating factors and conservation theorems for Hamilton’s canonical equations of motion of variable mass nonholonomic nonconservative dynamical systems[J].Chinese Physics，2002，11（8）：760-764.

[12]张毅，薛纭．Birkhoff系统的积分因子与守恒定理[J].力学季刊，2003，24（2）：280-285.

[13]Zhang Y.Integrating factors and conservation laws of generalized Birkhoff system dynamics in event space[J].Communications in Theoretical Physics（Beijing，China），2009，51（6）：1078-1082.

[14]束方平，张毅.用积分因子方法研究广义Birkhoff系统的守恒量[J].华中师范大学学报：自然科学版，2014，48（1）：42-45.

[15]Miller K S，Ross B.An Introduction to the Fractional Calculus and Fractional Differential Equations[M].New York：Wiley，1993.

[16]Podlubny I.Fractional Differential Equations[M].New York：Academic Press，1999.

Integrating factors and conserved quantities for Lagrange systems based on fractional order model

SHU Fangping1，ZHANG Yi2，ZHU Jianqing1
（1.School of Mathematics and Physics，SUST，Suzhou 215009，China；2.School of Civil Engineering，SUST，Suzhou 215011，China）

In order to further study the conserved quantities of mechanical systems based on fractional order model,we applied the method of integrating factors to the fractional order Lagrange system and proposed a new method for finding the conserved quantities of Lagrange systems based on fractional order model.First,we studied the necessary conditions for the existence of the conserved quantities of the fractional order Lagrange systems and the relation between the conserved quantities and the integrating factors.Second,the fractional order generalized Killing equations used to determine the integrating factors were presented.Finally,we obtained the conserved quantities of the Lagrange systems based on fractional order model.Besides,an example was given to illustrate the application of the results.

fractional order model；Lagrange system；integrating factor；conserved quantity

O316MR（2000）Subject Classification：00A69

A

1672－0687（2015）02－0001－05

责任编辑：谢金春

2014－10－22

国家自然科学基金资助项目（11272227）

束方平（1989-），女，江苏盐城人，硕士研究生，研究方向：力学中的数学方法。

*通信联系人：朱建青（1962-），男，教授，硕士生导师，E－mail：zjq@mail.usts.edu.com。