张静

（江苏科技大学 计算机科学与工程学院，江苏 镇江 212003）

粗糙集 （Rough Set）理论由波兰学者Z.Pawlak于1982年提出，是一种处理不精确、不相容和不完全数据的新的数学工具[1]。它已经在决策与分析、故障诊断、模式识别、数据挖掘、系统建模、动态目标识别及跟踪等领域取得了很大的成功[2]。属性约简是粗糙集理论的核心内容之一。目前已经出现了很多属性约简的方法，例如基于正区域的属性约简[3]、基于差别矩阵的属性约简[4]、基于信息熵的属性约简[5]、基于分布的属性约简及基于近似的属性约简[6]、基于云模型的约简方法[7]、基于相对粒度的约简算法发[8]等。本文通过将决策信息系统树形化，并定义了在此树形结构上的属性约简，发现属性可约简并不需要再次求得下上近似集，可直接由等价类所包含的决策属性来决定，由此可增加属性约简的效率。进而给出了一种基于编码解空间结构的求粗糙集属性约简最优解的算法，并发现编码解空间结构对求取最优解及次优解均有好处。

1 粗糙集中属性约简满足的条件

粗糙集的主要研究对象是决策表，一个决策表就是一个决策信息系统。下面是Pawlak关于决策表以及下上近似集的定义：

定义 1:五元组 S=（U，C，D，V，f）是一个决策表，其中 U={x1，x2，x3，…，xn}表示研究对象的非空有限集；D 表示决策属性C∪D→V是一个信息函数，它给U中每一个对象的所有属性赋予信息值，即对∀x∈U，a∈C∪D，有 f（x，a）∈Va；每一个属性子集P⊆（C∪D）决定了一个二元不可分辨关系：

IND（P）={（x，y）|（x，y）∈U×U，∀a∈P∧f（x，a）=f（y，a）}（1）

关系 IND（P）构成了 U的一个划分，用 U/IND（P）表示，简记为 U/P，U/P 中的元素[x]p={y|∀a∈P，f（x，a）=f（y，a）}称为 U关于P的等价类。

定义 2:在决策表 S=（U，C，D，V，f） 中， 设∀R⊆C∪D，X⊆U 记 U/R={R1|R2，…，RL}，则称 R（X）=U{Ri|Ri∈U/R，Ri⊆X}为 X 关于 R 的下近似集，R （X）=∪{Ri|Ri∈U/R，Ri∩X≠φ}为X关于R的上近似集。

根据下上近似集的定义可以得出下面两种基于统计意义的推理规则：如果对象x在R上的值满足某个条件，x就属于X（规则1）；如果对象x在R上的值满足某个条件，x就不属于 X（规则 2）。

考虑到这个因素，给出了下面两个粗糙集属性约简的定义：

定义 3:在决策表中 S=（U，C，D，V，f），若∀B⊆C，并且B（X）=C（X），B（X）=C（X）；∀b∈B 均有（B-{b}）（D）≠C（D）或者（B-{b}）（D）≠C（D），则称 B 是 C 相对于 D 的强属性约简。 所有C相对于D的属性强约简的集合记为StrongReduct（C，D）。

定义 4:在决策表中 S=（U，C，D，V，f），若∀B⊆C，并且B（X）=C（X）；∀b∈B 均有（B-{b}）（D）≠C（D），则称 B 是 C 相对于D的弱属性约简。所有C相对于D的属性弱约简的集合记为 WeakReduct（C，D）。

强属性约简可以保证约简后这两个规则都不变，而弱属性约简只能保证约简后规则1不变。为了得到通过等价类判断属性是否可被约简的规则，首先给出了决策信息系统的树形表示，以及树形表示约简算法。

2 决策信息系统的树形表示以及此树形表示约简的求解

决策信息系统的树形表示：

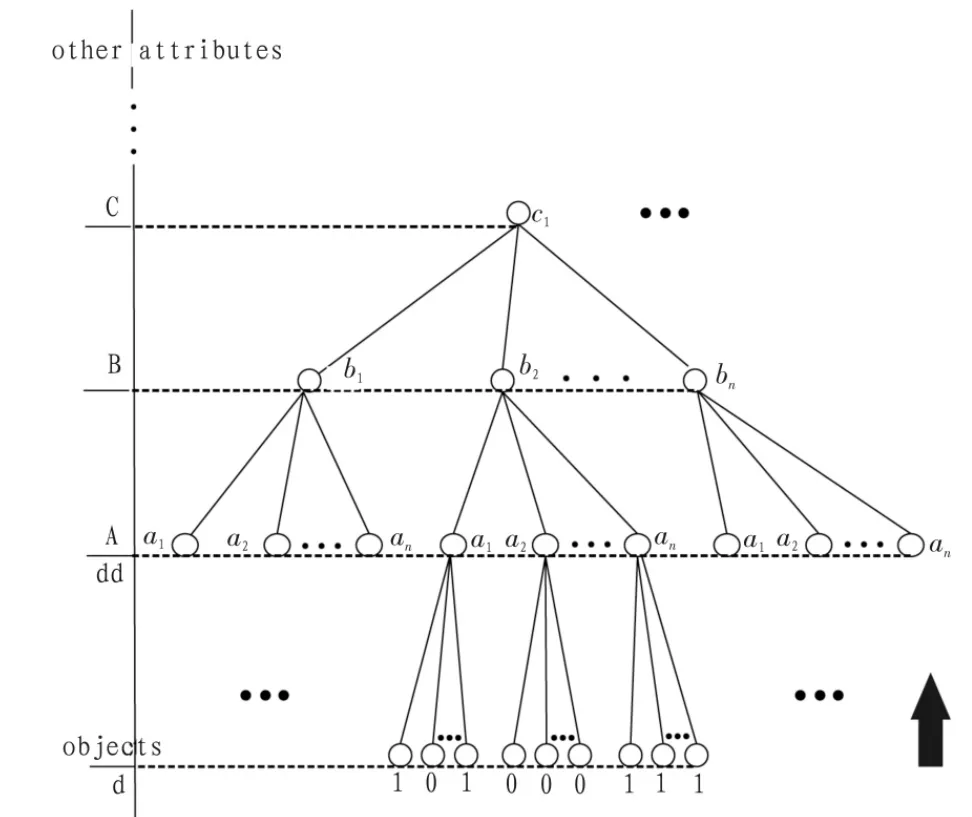
图1 决策信息系统树形表示图Fig.1 A tree representation of decision information system

此树（如图1所示）是依据不可分辨关系建立的。从上往下，除最后一层分别代表属性层，大写字母代表属性（为了以示和属性集合的区别用小一号的大写字母表示），小写字母代表属性的值。最后一层代表对象层，d代表此对象的决策属性值。根据此表示方法易得，从上至下的每一条路径pi（如…c1b1a2）代表着一个等价类。dd代表等价类的决策属性值。∀R⊆C，U/R={R1，R2，…，RL}表示由条件属性集R对论域U的划分，则根据不可分辨关系可建立双射pc:P→U/R，其中P={pi}。 dd（pi）=1 代表着等价类 pc（pi），pc（pi）⊆R（X）；dd（pi）=2 代表着等价类 pc（pi），pc（pi）⊆R（X）；dd（pi）=0 代表着等价类 pc（pi），pc（pi）⊆R（XC）。 若 x 是决策信息系统中的一个对象（处于决策信息系统树形图的最底层），则 dd（x）=d（x）。

决策信息系统的树形表示约简算法：

定义 5:在决策表 S=（U，C，D，V，f）中，A∈C，pi是一条路径且最后一个节点是属性A中的值如:

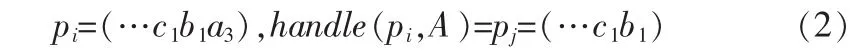
令Path（A）最后一个节点是属性A中的值得路径的集合，∀pi，pj∈Path（A），则 handle（pi，A）=handle（pj，A）。

易证，∀pi，pj∈Path（A），pc（pi）⊆pc（handle（pi，A））并 且pc（pj）⊆pc（handle（pj，A））。 下面给出由 dd（pi）和 dd（pj）求dd（handle（Path（A）））的算法，如图 2 所示（易证）：

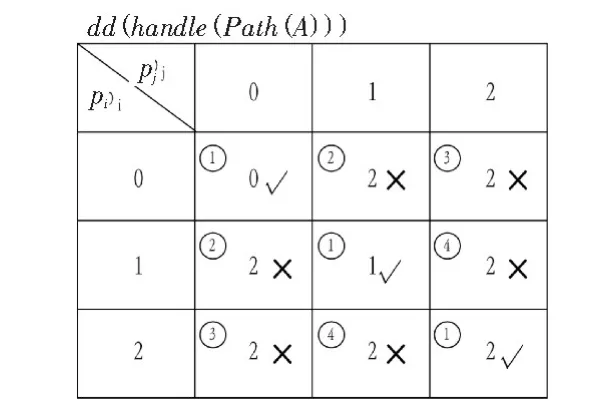
图 2 dd（handle（path（A）））的取值表Fig.2 Value table of dd（handle（path（A）））

其中 2 的情况会同时缩小（C-{A}）（X）和（C-{A}）（XC）（如图 3 所示）；3 的情况会缩小 （C-{A}）（XC）；4 的情况会缩小（C-{A}）（X）；只有 1 的情况是满足约简条件的（如图 4）。所以当满足2、3、4的时候属性不可以被强约简，只有满足①的情况属性A才能被强约简。这个结论也是易证的。有了这个结论我们就可以仅仅通过等价类和决策属性就可以判断在此树形表示中是否可被约简。

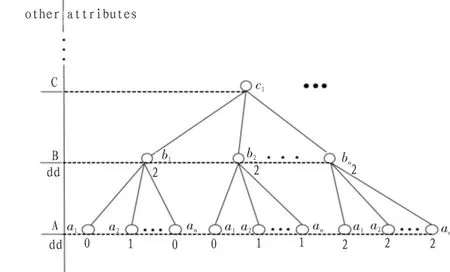
图3 属性A不可被强约简图Fig.3 Unable to be strong reduction graph of A

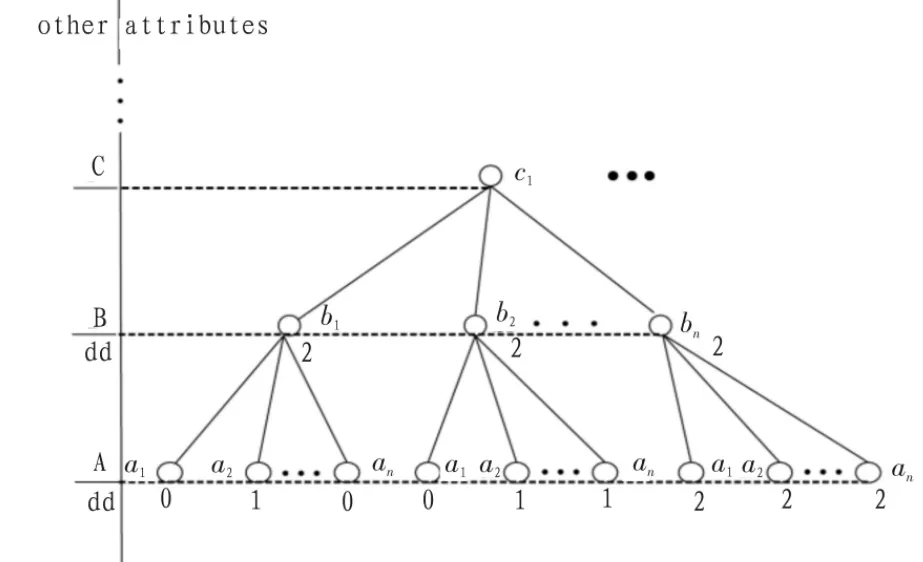
图4 属性A可被强约简图Fig.4 Can be strong reduction graph of A

根据树形表示与等价类之间的关系可得若某属性在此表示下可被强约简则，它必可在决策信息系统中也可被强约简；若某属性在此表示下不可被强约简则，它必可在决策信息系统中也不可被强约简。

对每一个属性强约简（RE，C-RE），其中C-RE是强约简掉的属性，RE是保留下来的属性。Random（RE）是保留下来的属性的随机排列，Random（C-RE）是强约简掉的属性的随机排列（Random（RE），Random（C-RE））。 根据排列可以画出一个属性强约简的树形图，并根据此树形图的属性约简又可得到最终的属性约简。（易证）

3 树形表示属性约简分析

定义 6:在决策表 S=（U，C，D，V，f） 中，C 相对于 D 属性强约简的核集定义为

在依据决策系统树形图的属性约简中，令C相对于D第一次不可被强约简的属性的集合为NStrongfirst（C，D）。

证明：①∀NSfi∈NStrongfirst（C，D）⇒NSfi∈StrongCore（C，

使用反证法：若∀NSfi∉∩REj，则∃j，NSfi∉REj即 NSfi可以被约简，由于属性的约简与顺序无关。所以NSfi可被第一次约简。矛盾所以式子成立。

②∀SCi∈StrongCore（C，D）⇒SCi∈NStrongfirst（C，D）

若∀SCi∈StrongCore（C，D），SCi不可被任何约简，自然不可被第一次约简，即SCi∈NStrongfirst（C，D）。 定理证明完毕。

定义 7:在决策表 S1=（U1，C1，D1，V1，f1）中，A1⊆C1，B1⊆C1且 A1∪B1=C1，其中 B1={b1，b2，…，bn}。 在决策表 S2=（U2，C2，D2，（V1）bn}，∀x∈U2，若 a∈A1∪D1， f2（x，a）=f1（x，a）；若 a=b，f2（x，b）=（ f1（x，b1），f1（x，b2），…，f1（x，bn））。向这样通过 S1定义 S2的过程称为决策表 S1的属性合并， 记为 S2=AmalAttr（S1，B，b）。其中b是由B合并的属性。

定理二：有决策表 S1=（U1，C1，D1，V1，f1）、决策表 S2=（U2，C2，D2，V2，f2） 以及属性集合 A1、B， 其中 A1⊆C1，B⊆C1，A1∪B=C1，S2=AmalAttr（S1，B，b），则 C2=A1∪b，IND（S1）=IND（S2）。由决策表的属性合并的定义以及不可分辨关系的定义很容易证。

由上面两条定理可得如下推论：

推论 1：有决策表 S=（U，C，D，V，f），以及属性集合 A⊆C和B⊆C，其中A⊆B，如果A不可被约简，则B也不可被约简。

证明：S1=AmalAttr （S，A，a）=（U1，C1，D1，V1，f1）， 其中 C1=（C-A）∪{a}。 由定理二可知 IND（S）=IND（S1）。 根据上下近似集的定义可知 C（X）=C1（X），C（X）=C1（X）。 由于 C1-{a}=C-A，根据属性合并的定义可知 （C1-{a}）（X）=（C-A）（X），（C1-{a}）（X）=（C-A）（X）。由属性约简的定义可知若A在S中不可约，则 a 在 S1中不可约。那么 a∈NStrongfirst（C1，D1）。根据定理一可知 a∈StrongCore（C1，D1），所以在 S1中任何包含 a 的属性集都不可约。所以（B-A）∪{a}在S1中不可约。根据属性合并的定义可知（C1-（B-A）∪{a}）（X）=（C-B）（X），（C1-（B-A）∪{a}）（X）=（C-B）（X）。 又由于 C（X）=C1（X），C（X）=C1（X），根据属性约简的定义可知若（B-A）∪{a}在S1中不可约，则B在S中不可约。证毕。

通过以上的分析可知，某一个属性子集是否可被强约简可通过在此信息系统中将此属性子集合并后得到的信息系统中，由此属性子集生成的新的属性在该信息系统树形表示中是否可被第一次强约简决定。由于在信息系统树形表示中属性的约简只由等价类和决策属性就可以决定了，所以在信息系统中也可以通过等价类以及决策属性就可以决定了。

若这个属性子集不可被强约简，则包含它的属性子集也不可被强约简（即可被剪枝，假设属性只有ABCD，则属性子集的剪枝过程如图5所示）。若在信息系统树形表示中不能被第一次强约简，则该属性属于信息系统属性强约简的核中。核是不可被约简的属性，除核之外的属性都是可被约简的属性。

图5 属性子集剪枝过程图Fig.5 Attribute subset pruning process diagram

4 结 论

属性约简在粗糙集理论研究中发挥着巨大的作用。本文从树形结构考虑给出了决策信息系统的树形表示。基于本文提出的树形结构文中进一步的得出了一个判断属性是否可被约简的好的方法，通过理论分析，本文提出的属性约简算法可以大大的减少属性搜索的步骤从而降低属性约简所需要的时间。

[1]Pawlak Z.Rough Sets-theoretical aspects of reasoning about data[M].Kluwer Acadamic Publisher，1991.

[2]Pawlak Z.A rough set view on Bayes’theorem[J].International Journal of Intelligent Systems，2003，18（5）:487-498.

[3]Pawlak Z.Rough set[J].Communication of the ACM，1995，38（11）:89-95.

[4]Skowron A，Rauszer C.The discernibility matrices and functions in information systems[M].Intelligent Decision Support Handbook of Applications and Advances of the Rough Sets Theory.Kluwer Academic Publishers，1992.

[5]Wang G Y，Yu H，Yang D C.Decision table reduction based on conditional information entropy[J].Chinese Journal of Computer，2002，25（7）:759-766.

[6]Zhang W X，Mi J S，Wu W Z.Knowledge reductions in inconsistent information systems[J].Chinese Journal of Computer，2003，26（1）:12-18.

[7]代劲，何中市.基于云模型的决策表规则约简[J].计算机科学，2010，37（6）:265-267.DAI Jin，HE Zhong-shi.Rules reduction for decision table based on cloud model[J].Computer Science，2010，37（6）:265-267.

[8]徐久成，史进玲，孙林.一种基于相对粒度的决策表约简算法[J].计算机科学，2009，36（3）:205-207.XU Jiu-cheng，SHI Jin-ling，SUN Lin.Attribute reduction algorithm based on relative granularity in decision tables[J].Computer Science，2009，36（3）:205-207.