邹广玉

（长春工程学院理学院，长春130012）

0 引言及主要结论

设｛Xn，n≥1｝是一随机变量列，记设Tn是一个统计量（或随机函数），可以表示成

其中an＞0是常数列，Rn称为余项。很多常用的统计量（或随机函数）可被表示成式（1）的形式，例如U统计量、线性过程、线性模型的误差方差估计量等。本文将讨论这类统计量的乘积的某些极限性质。

几乎处处中心极限定理（ASCLT）是近几十年来概率论研究的一个热门方向，由Schatte（1988）在文献［1］中最早开始研究，在独立同分布情况下，在比EX1＝0，EX＝1稍强的条件下证明了

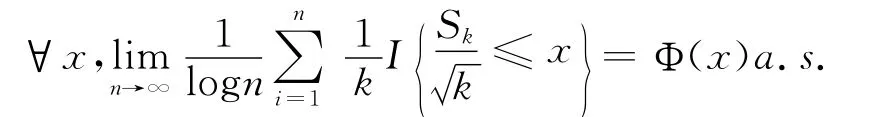
式中：Φ（x）为服从 N（0，1）的随机变量的分布函数；I（·）为示性函数，下同。

这一结果后来被称为独立同分布随机变量列的几乎处处中心极限定理，此后众多学者对几乎处处中心极限定理进行了研究。文献［2］讨论了当｛Xn，n≥1｝为独立同分布随机变量列时Tn的乘积的几乎处处中心极限定理，本文在此基础上得到了｛Xn，n≥1｝为严平稳NA序列时Tn的乘积的几乎处处中心极限定理。

定义1 称随机变量序列｛Xi，i∈I｝是负相伴（简称NA）的，如果对于任何两个使得协方差存在且对每个变元均非降的函数G与H，都有

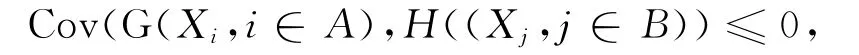
式中I＝ ｛1，…，n｝，A、B为I的两个不交子集。

称随机变量序列｛Xi，i∈N｝是NA的，如果对任何n≥2，X1，…，Xn都是NA的。

NA序列的定义是20世纪80年代由Alam和Saxena在文献［3］给出的，它是包含独立随机变量序列在内的更为广泛的相依随机变量类型，在可靠性理论、渗透性理论及多元分析中有重要作用，因此研究其极限性质具有重要意义。本文的结论如下。

定理1 设｛Xn，n≥1｝是正的严平稳的NA随机变量列，满足EX1＝μ＞0和VarX1＝σ2＜∞，记变异系数其中an＞0是常数列，并假设下面条件成立

（1）对 某 个 ε ＞ 0，｜ Cov（X1，Xn＋1）｜＝O（n－1（logn）－2－ε），

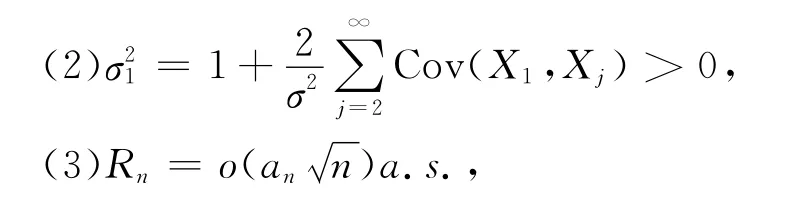
那么

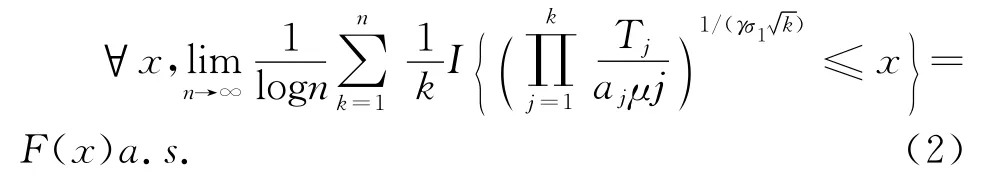
1 若干引理

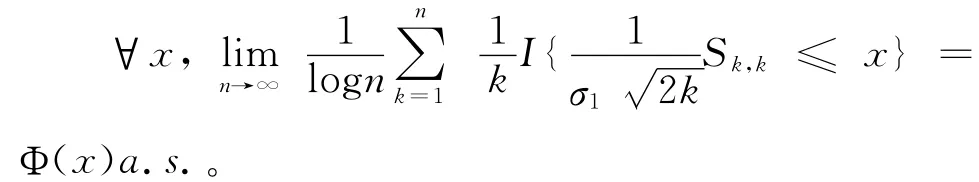
引理2［4］设｛Xn，n≥1｝是严平稳的NA随机变量列，满足EX1＝0和，且下文中的C在不同地方代表不同的常数。我们在证明过程中需要下面几个引理。

引理1［4］在定理的假设条件下，有｜Cov（X1，Xj）｜＜ ∞，则对任意的0＜p＜2，有

Sn／n1／p→0，a.s. 当n→ ∞ 时。

引理3 在定理的假设条件下，有

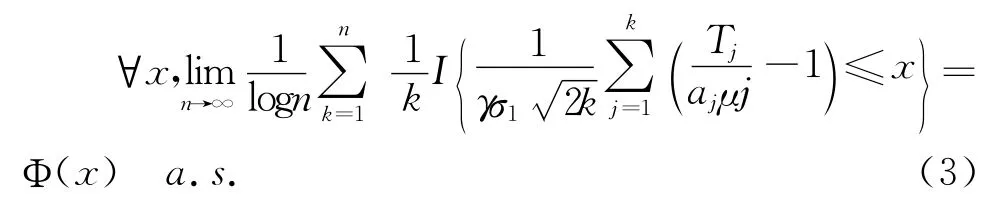
证明：

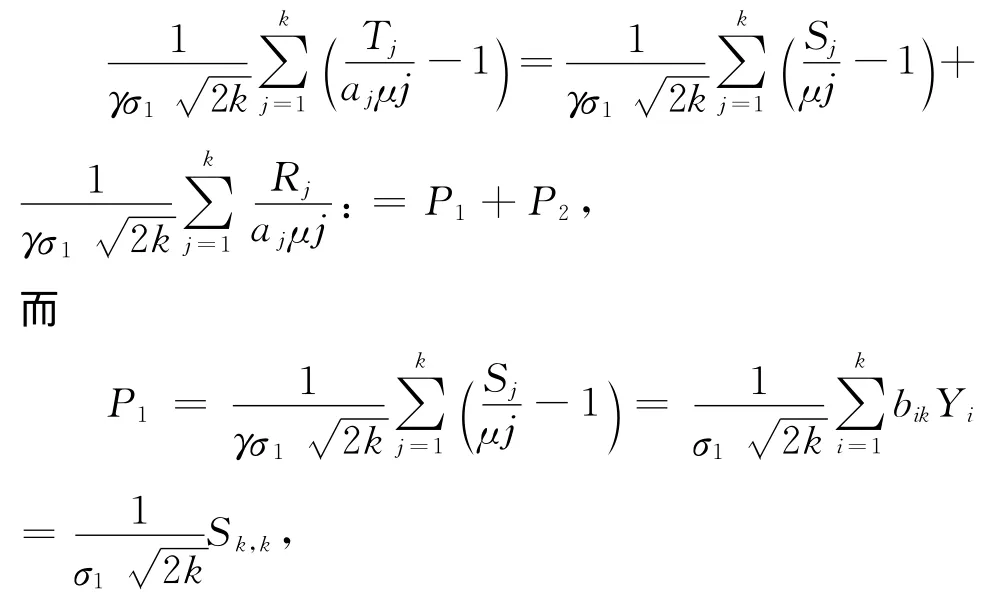
由引理1，有

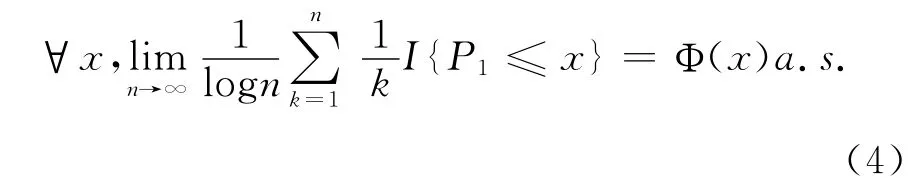
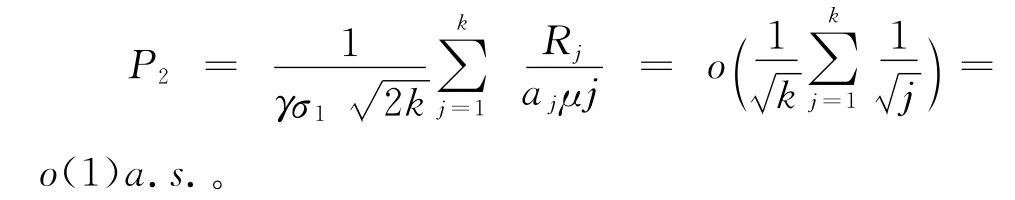
于是，对几乎所有的样本点ω和任意小的ε＞0，存在正整数N1＝N1（ω，ε，x），使得当k＞N1时有

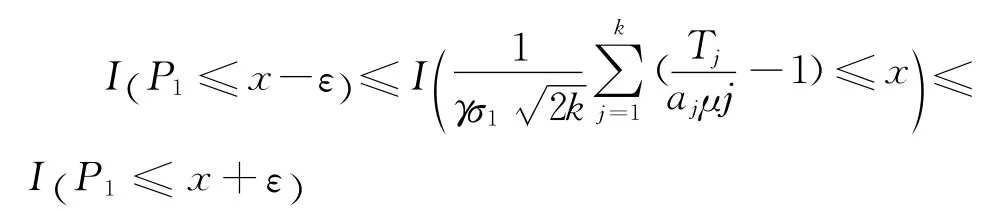
这样由式（4）可知式（3）成立，于是证明了引理3。

2 定理的证明

注意到式（2）等价于

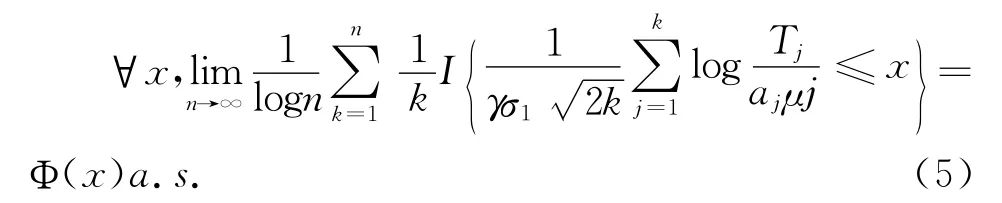
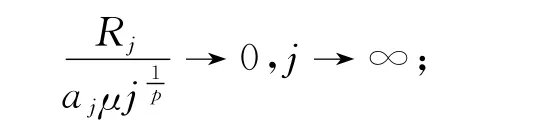
又由引理1知，对于充分大的j，有

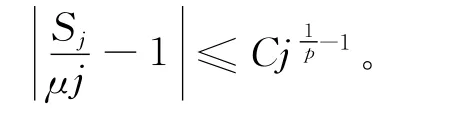
于是，对于充分大的j，有

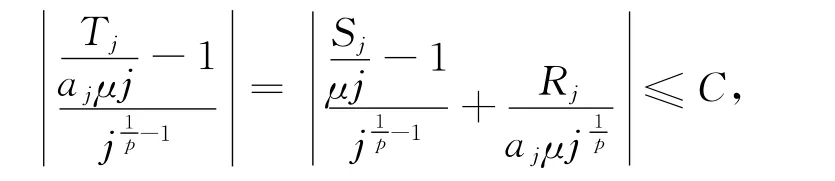
且当x→0时，log（1＋x）＝x＋O（x2），故有

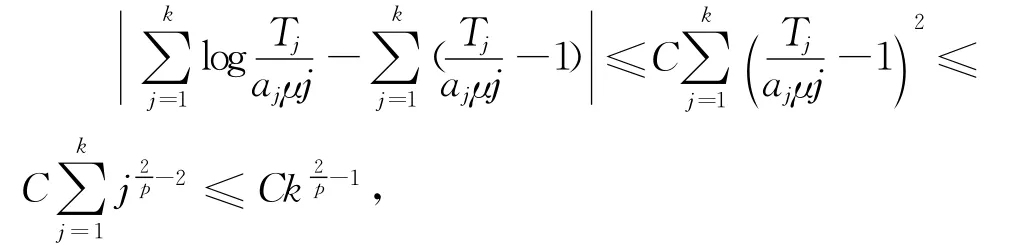
于是，对几乎所有的样本点ω和任意小的ε＞0，存在正整数N2＝N2（ω，ε，x），使得当k＞N2时有

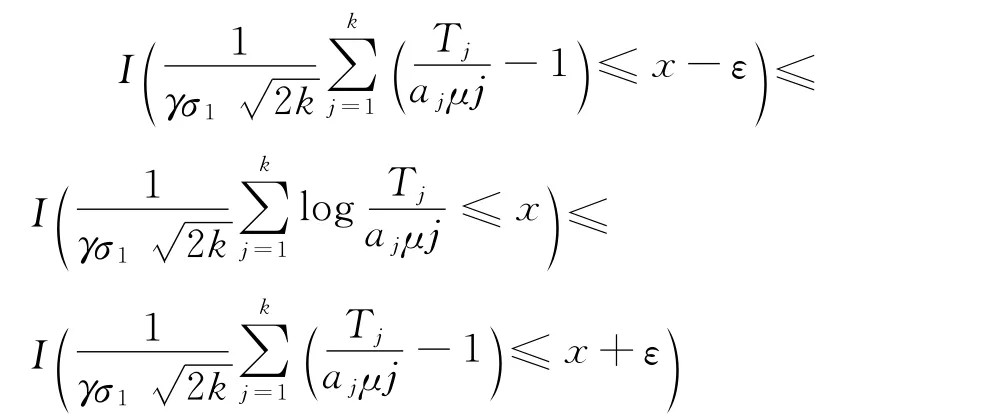
由引理3即知式（5）成立，这样就证明了定理。

［1］Schatte P.On strong versions of the central limit theorem［J］.Math.Nachr.，1988，137：249－256.

［2］邱瑾，陆传荣.一类统计量的乘积的渐近性质和几乎处处中心极限定理［J］.数学物理学报，2013，33（A）：3，475－482.

［3］Alam K，Saxena K M L.Positive dependence in multivariate distributions［J］.Comm.Statist.Theory Math，1981，A10（12）：1183－1196.

［4］LI Yun－xia，WANG Jian－feng.An almost sure limit theorem for products of sums under association［J］.Statist.Probab.Lett.，2008，78（4）：367－375.