SHANKAR B. M.

Department of Mathematics, PES Institute of Technology, Bangalore 560 085, India, E-mail: bmshankar@pes.edu KUMAR Jai

ISRO Satellite Centre, Bangalore 560 017, India

SHIVAKUMARA I. S.

Department of Mathematics, Bangalore University, Bangalore 560 001, India

NG Chiu-On (吴朝安)

Department of Mechanical Engineering, The University of Hong Kong, Hong Kong, China

Stability of fluid flow in a Brinkman porous medium-A numerical study*

SHANKAR B. M.

Department of Mathematics, PES Institute of Technology, Bangalore 560 085, India, E-mail: bmshankar@pes.edu KUMAR Jai

ISRO Satellite Centre, Bangalore 560 017, India

SHIVAKUMARA I. S.

Department of Mathematics, Bangalore University, Bangalore 560 001, India

NG Chiu-On (吴朝安)

Department of Mechanical Engineering, The University of Hong Kong, Hong Kong, China

(Received November 27, 2013, Revised May 5, 2014)

The stability of fluid flow in a horizontal layer of Brinkman porous medium with fluid viscosity different from effective viscosity is investigated. A modified Orr-Sommerfeld equation is derived and solved numerically using the Chebyshev collocation method. The critical Reynolds numbercRe, the critical wave numbercα and the critical wave speedcc are computed for various values of porous parameter and ratio of viscosities. Based on these parameters, the stability characteristics of the system are discussed in detail. Streamlines are presented for selected values of parameters at their critical state.

Brinkman model, Chebyshev collocation method, hydrodynamic stability, modified Orr-Sommerfeld equation

Introduction

The stability of fluid flows in a horizontal channel has been studied extensively and the copious literature available on this topic has been well documented in the book by Drazin and Reid[1]. The interesting finding is that the Poiseuille flow in a horizontal channel becomes unstable to infinitesimal disturbances when the Reynolds number exceeds the critical value 5 772. The corresponding problem in a porous medium has attracted limited attention of researchers despite its wide range of applications in geothermal operations, petroleum industries, thermal insulation and in the design of solid-matrix heat exchangers to mention a few. In particular, with the advent of hyperporous materials there has been a substantial increase in interest in the study of stability of fluid flows through porous media in recent years as it throws light on the onset of macroscopic turbulence in porous media[2].

The hydrodynamic stability of flow of an incompressible fluid through a plane-parallel channel or circular duct filled with a saturated sparsely packed porous medium has been discussed on the basis of an analogy with a magneto-hydrodynamic problem by Nield[3]. Awartani and Hamdan[4]considered the stability of plane, parallel fully developed flow through porous channels and studied the effects of porous matrix and the microscopic inertia. The influence of slip boundary conditions on the modal and nonmodal stability of pressure-driven channel flows was studied by Lauga and Cossu[5]. By employing the Brinkman model with fluid viscosity same as effective viscosity, Makinde[6]investigated the temporal development of small disturbances in a pressure-driven fluid flow through a channel filled with a saturated porous medium. The critical stability parameters were obtained for a wide range of porous medium shape factor parameter. Besides, Makinde and Motsa[7]analyzed small disturbance stability of hydromagnetic steady flow between two parallel plates at a very small magnetic Reynolds number, while Makinde and Mhone[8]investigated the temporal stability of magneto-hydrodynamic Jeffery-Hamel flows at very small magnetic Reynolds number.

Fig.1 Physical configuration

1. Mathematical formulation

We consider the flow of an incompressible viscous fluid through a layer of sparsely packed porous medium of thickness 2h, which is driven by an external pressure gradient. The bounding surfaces of the porous layer are considered to be rigid and a Cartesian coordinate system is chosen such that the origin is at the middle of the porous layer as shown in Fig.1.

The governing equations are

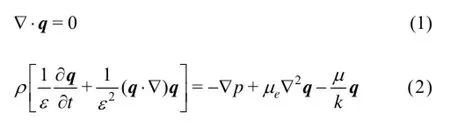
where q=(u,0,w) the velocity vector, ρ the fluid density, p the pressure, μethe effective viscosity, μ the viscosity of the fluid, k the permeability and ε the porosity of the porous medium. Let us render the above equations dimensionless using the quantities

Substituting Eq.(9) into Eqs.(4) and (5), linearizingand restricting our attention to two-dimensional disturbances, we obtain (after discarding the asterisks for simplicity)

To discuss the stability of the system, we use the normal mode solution of the form

where =d/dDz is the differential operator. First, the pressure p is eliminated from the momentum equations by operating D on Eq.(15), multiplying Eq.(16) by iα and subtracting the resulting equations and then a stream function (,,)x z tψ is introduced through

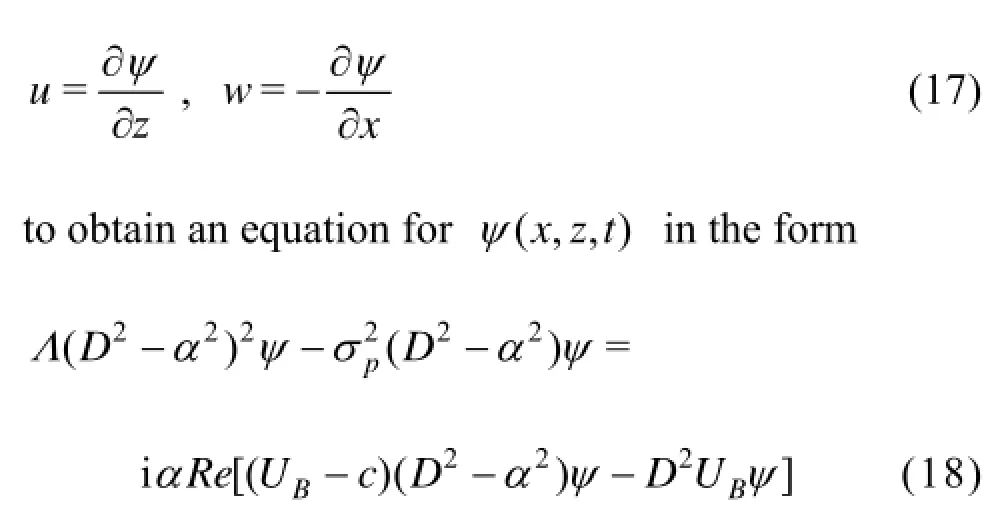
Equation (18) is the required stability equation which is the modified form of Orr-Sommerfeld equation and reduces to the one obtained for an ordinary viscous fluid if σp=0 and Λ=1.

The boundaries are rigid and the appropriate boundary conditions are

2. Method of solution

Equation (18) together with the boundary conditions (19) constitutes an eigenvalue problem which has to be solved numerically. The resulting eigenvalue problem is solved using the Chebyshev collocation method.

Table 1 Order of polynomial independence for σp=0.5, Re=20000, α=1 and Λ=1

The thk order Chebyshev polynomial is given by

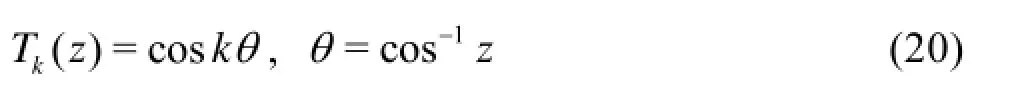
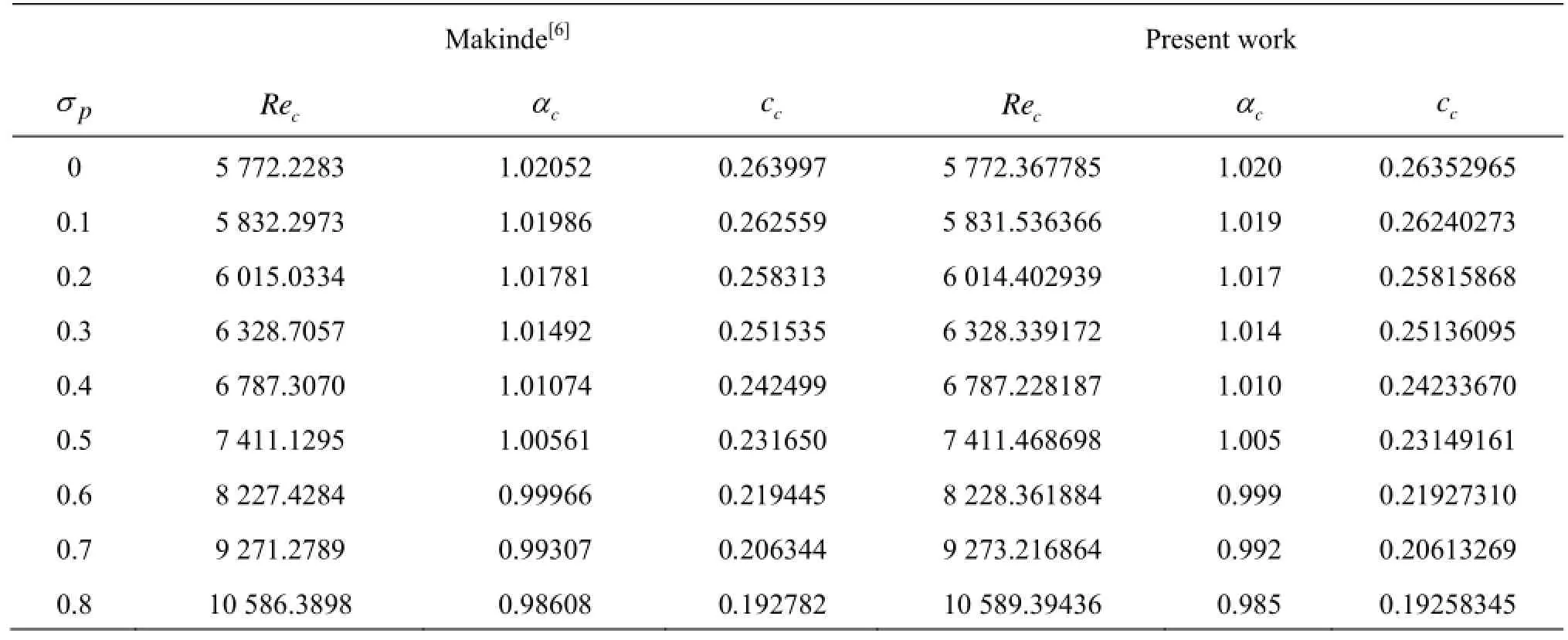
Table 2 Comparison of critical stability parameters for values of A=Reε2(-dpb/dx) =2 and Λ=1

The Chebyshev collocation points are given by

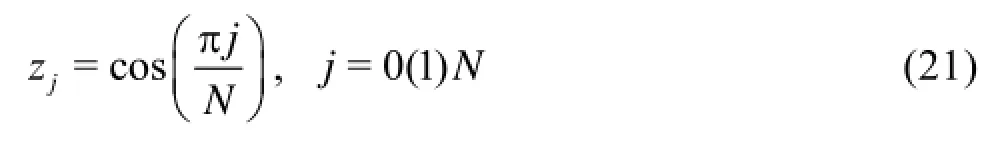
Here, the upper and lower wall boundaries correspond to j=0 and N, respectively. The field variable ψ can be approximated in terms of the Chebyshev variable as follows

The governing Eqs.(18) and (19) are discretized in terms of the Chebyshev variable z to get

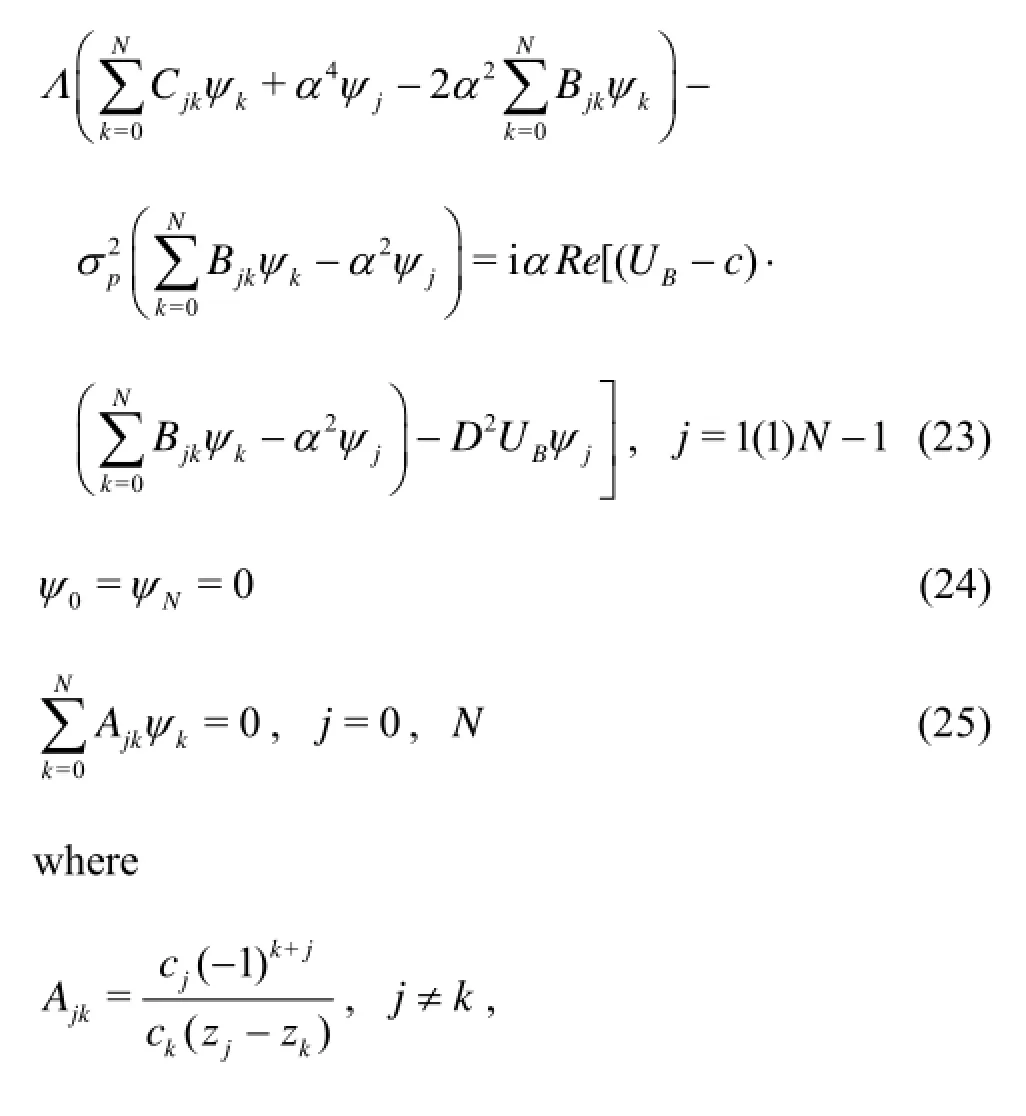
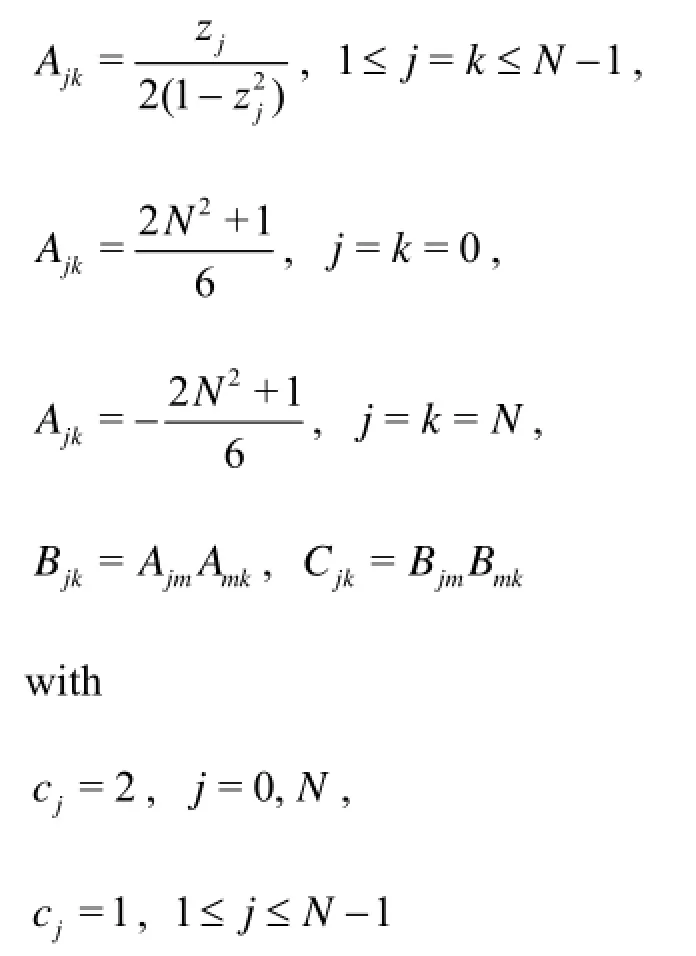
The above equations form the following system of linear algebraic equations

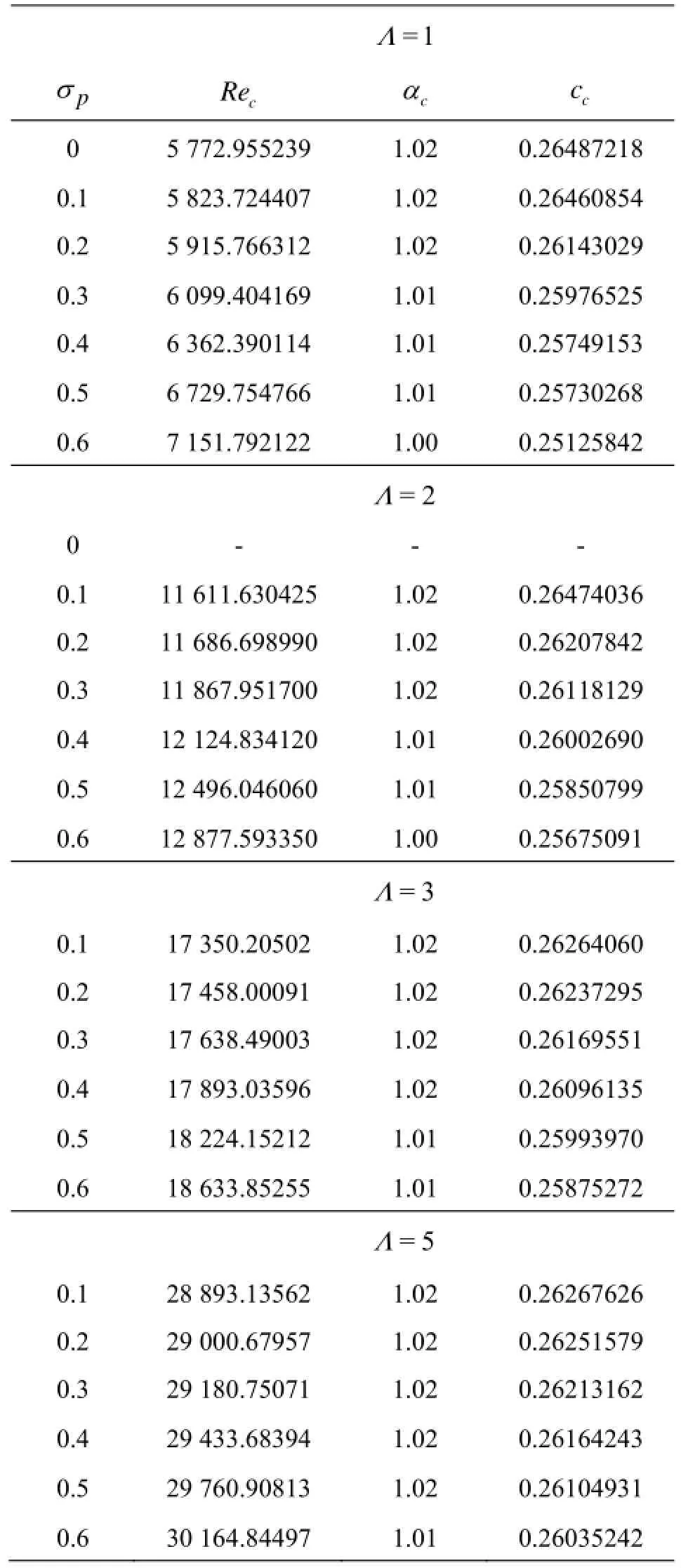
Table 3 Variation of Rec, αcand ccfor different values of σpand Λ

For fixed values of Λ, σpand Re, the values of c which ensure a non-trivial solution of Eq.(28) are obtained as the eigenvalues of the matrix B-1A From N+1 eigenvalues c(1),c(2),…,c( N+1), the one having the largest imaginary part of (c( p), say) is selected. In order to obtain the neutral stability curve, the value of Re for which the imaginary part of c( p) vanishes is sought. Let this value of Re be Req. The lowest point of Reqas a function of α gives the critical Reynolds number Recand the critical wave number αc. The real part of c( p) corresponding to Recand αcgives the critical wave speed cc. This procedure is repeated for various values of Λ and σp.

3. Results and discussion

The stability of fluid flow in a horizontal layer of Brinkman porous medium with fluid viscosity different from effective viscosity is investigated using the Chebyshev collocation method. To know the accuracy of the method employed, it is instructive to look at the wave speed as a function of order of Chebyshev polynomials. Table 1 illustrates this aspect for different orders of Chebyshev polynomials ranging from 1 to 100. It is observed that four digit point accuracy was achieved by retaining 51 terms in Eq.(22). As the number of terms increases in Eq.(22), the results are found to remain consistent and the accuracy improved up to 7 digits and 10 digits for N=80 and N=100, respectively. In the present study, the results are presented by taking N=80 in Eq.(22). To compare our results with those of Makinde[6], the results obtained for different values of porous parameter for a fixed value of A=Reε2(-dpb/dx)=2 and Λ=1 are tabulated in Table 2. The results are in good agreement and confirm the validity of numerical method employed.

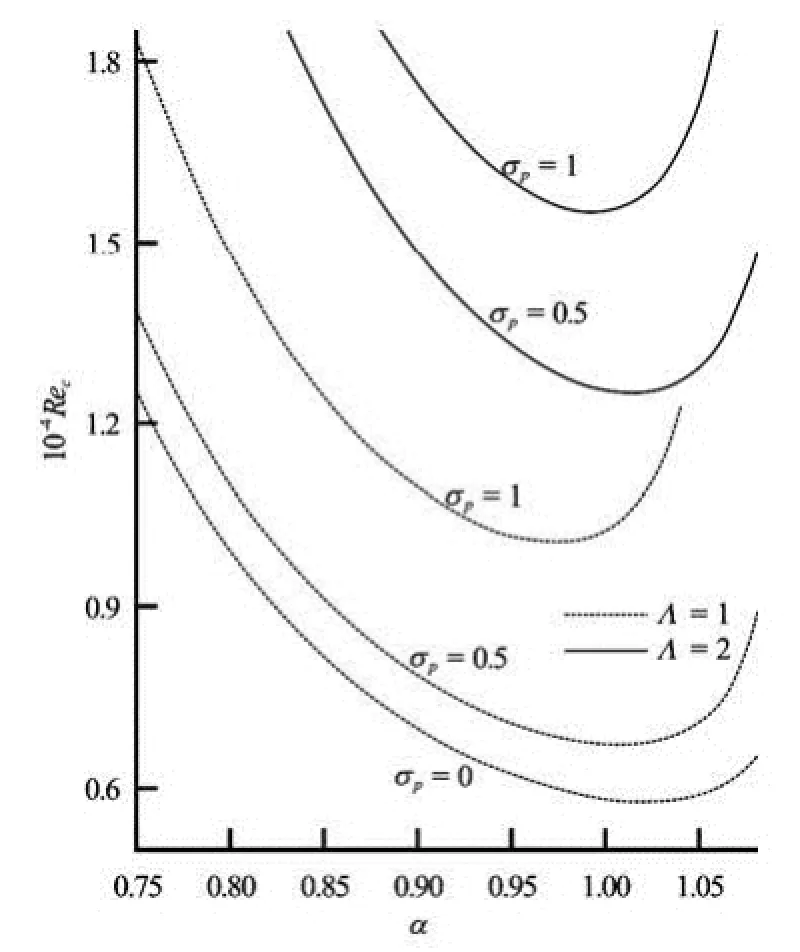
Fig.2 Neutral curves for different values of pσ and Λ

Fig.3 Variation of pσ for two values of Λ

As was pointed out in the introduction, the Brinkman model rests on an effective viscosity μedifferent from fluid viscosity μ denoted through Λ in dimensionless form and it has a determinative influence on the stability of the system. The critical stability parameters computed for various values of Λ=1, 2, 3 and 5 as well as porous parameter σpare tabulated in Table 3. The results for σp=0 and Λ=1 in Table 3 correspond to the stability of classical plane-Poiseuille flow. For this case, it is seen that the critical Reynolds number Rec=5772.955239, the critical wave number αc=1.02 and the critical wave speed cc=0.264872176035885which are in excellent agreement with those reported in the literature[1]. From the table it is obvious that increasing Λ is to increase Recsignificantly though not αcand cc. Thus increase in Λ has a stabilizing effect on the fluid flow due to increase in the viscous diffusion. Besides, increase in the porous parameter is to increase Recand thus it has a stabilizing effect on the fluid flow due to decrease in the permeability of the porous medium.

The neutral stability curves are displayed in Fig.2 for different values of σpand for two values of Λ=1 and 2. The portion below each neutral curve corresponds to stable region and the region above corresponds to instability one. It may be noted that, increase in σpand Λ is to increase the region of stability. The lowest curve in the figure corresponds to the classical plane-Poiseuille flow case.

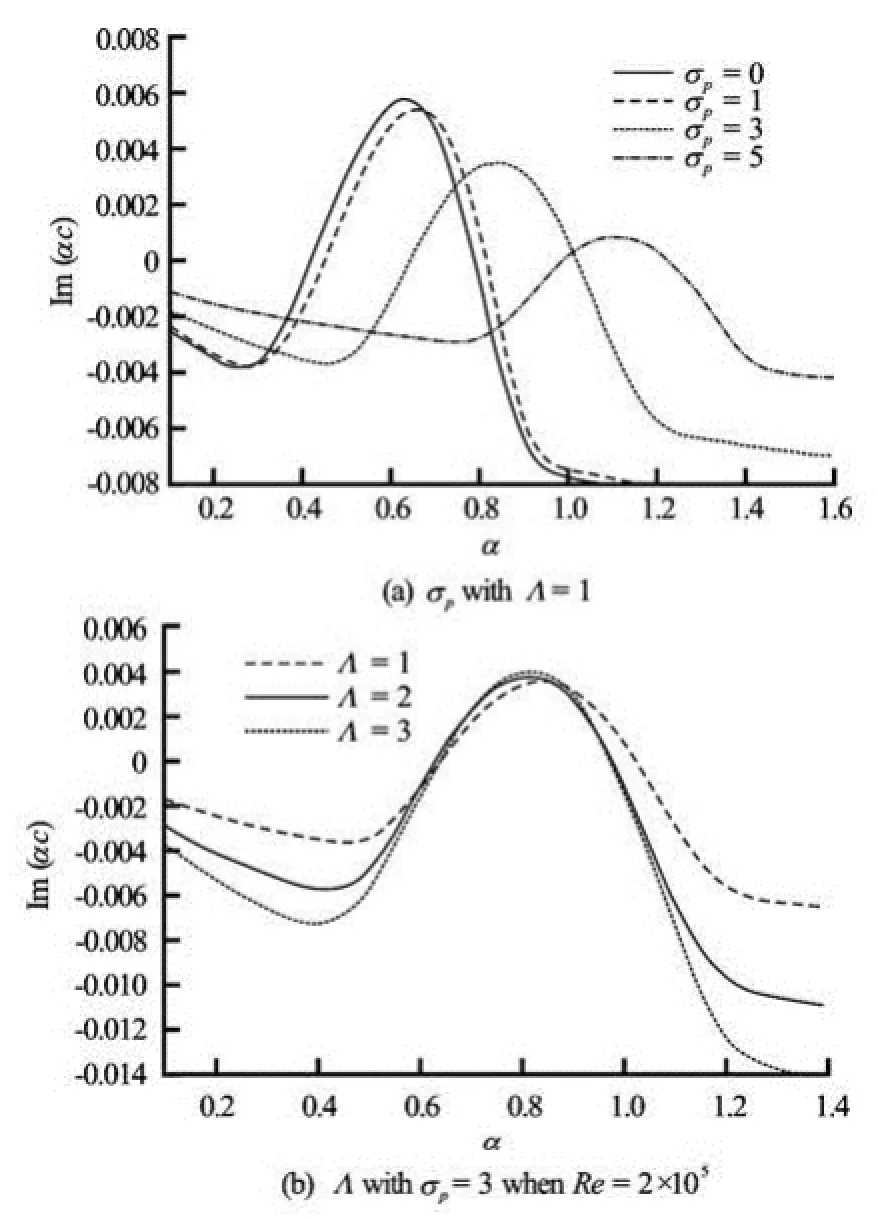
Fig.4 Variation of growth rate Im(αc) against α for different values

Figures 3(a), 3(b) and 3(c), respectively, show the variation of Rec, αcand ccas a function of porous parameter σpfor two values of Λ=1 and 2. It is observed that increase in σpand Λ is to reinforce stability on the system. The critical wave number exhibits a decreasing trend initially with σpbut increases with further increase in σp. Although initially the critical wave number for Λ=2 are higher than thoseof Λ=1, the trend gets reversed with increasing values of σp. The critical wave speed decreases with increasing porous parameter (σp=0 to 10) and remains constant as σpincreases further. Moreover, the critical wave speed decreases with increasing Λ and becomes independent of ratio of viscosities with increasing porous parameter.

Fig.5 Streamlines for =1Λ

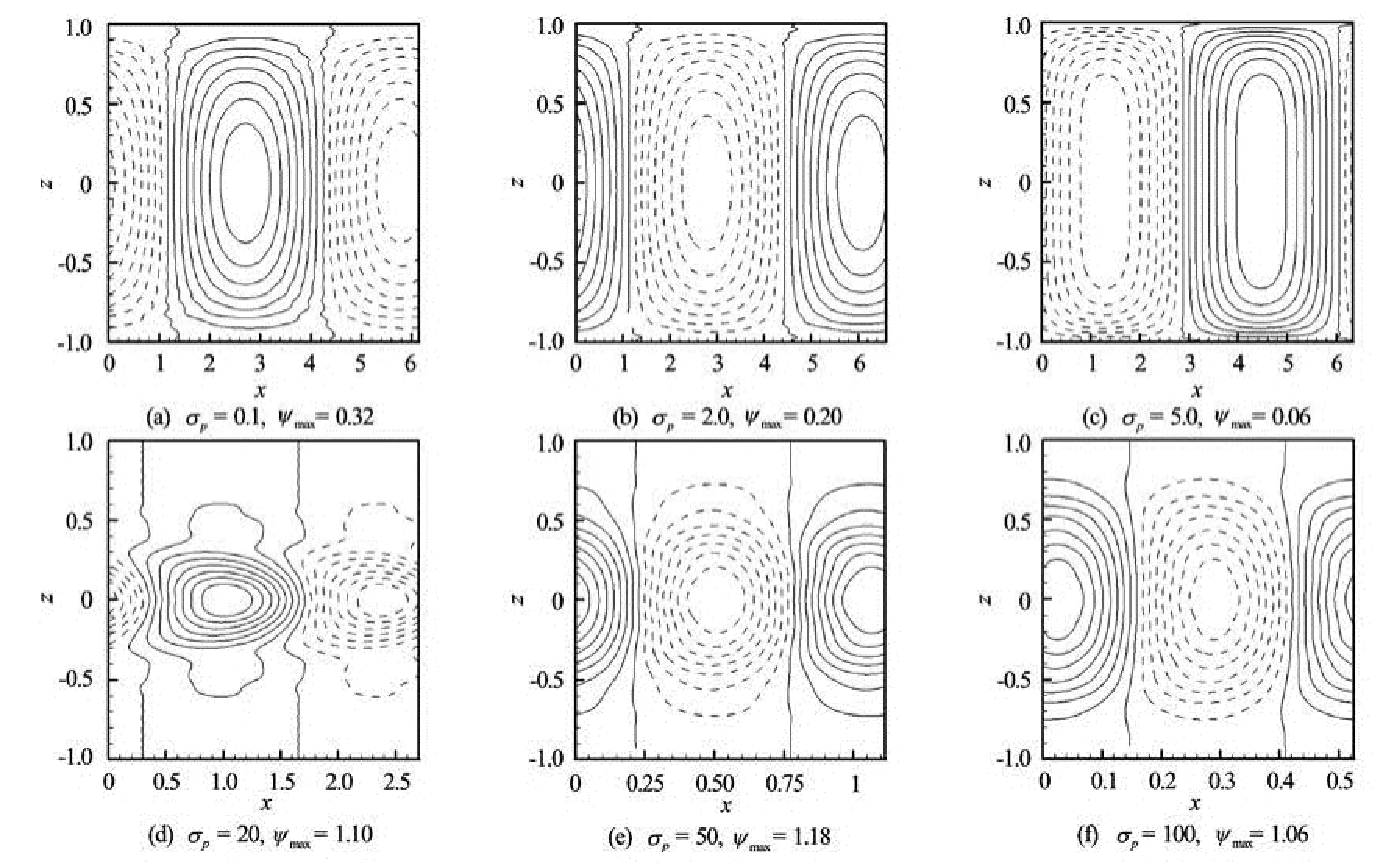
Fig.6 Streamlines for =2Λ

The variation in the growth rate of the most unstable mode against the wave number for different values of porous parameter with Λ=1 and for different values of ratio of viscosities with σp=3 is illustrated in Figs.4(a) and 4(b), respectively. It is observed that increase in the value of porous parameter is to suppre-ss the disturbances and thus its effect is to eliminate the growth of small disturbances in the flow. Although similar is the effect with increasing the value of ratio of viscosities at lower and higher wave number regions, an opposite kind of behavior could be seen at intermediate values of wave number.

Figures 5 and 6 show the streamlines for different values of σpfor Λ=1 and 2, respectively at their critical state. In the figures, dashed and solid lines represent negative and positive values, of ψ, respectively. It is observed that there is a significant variation in the streamlines pattern with varying σpand Λ. As the value of σpincreases from 0 to 5, the strength of secondary flow decreases but flow profile remains same. In this regime, convective cells are unicellular and cells are spread throughout the domain. Figure 5(d) indicates that for σp=20, secondary flow becomes double-cellular but flow is only near to walls of the channel. But it is not true for Λ=2 for the same σp. As the value of σpincreases further the flow strength again increases and convective cells become unicellular. The streamlines pattern illustrated in Fig.6 for Λ=2 exhibits a similar behavior.

4. Conclusion

The temporal development of infinitesimal disturbances in a horizontal layer of Brinkman porous medium with fluid viscosity different from effective viscosity has been studied numerically using the Chebyshev collocation method. It is found that the ratio of viscosities has a profound effect on the stability of the system and increase in its value is to stabilize the fluid flow. Nonetheless, its effect on the critical wave number and the critical wave speed is found to be insignificant. Besides, increase in the value of porous parameter has stabilizing effect on the fluid flow. The secondary flow for =Λ1 and 2 is spread throughout the domain at lower values ofpσ but confined in the middle of the domain at higher values. Secondary flow pattern remains the same for both values of viscosity ratios considered here.

Acknowledgements

The author B. M. S. wishes to thank the Head of the Department of Science and Humanities, Principal and the Management of the College for Encouragement. The authors wish to thank the reviewers for their useful suggestions.

[1] DRAZIN P. G., REID W. H. Hydrodynamic stability[M]. Cambridge, UK: Cambridge University Press, 2004.

[2] INGHAM D. B., POP I. Transport phenomena in porous media II[M]. Oxford, UK: Elsevier Science, 2002, 198-230.

[3] NIELD D. A. The stability of flow in a channel or duct occupied by a porous medium[J]. International Journal of Heat and Mass Transfer, 2003, 46(22): 4351-4354.

[4] AWARTANI M. M., HAMDAN M. H. Fully developed flow through a porous channel bounded by flat plates[J]. Applied Mathematics and Computation, 2005, 169(2): 749-757.

[5] LAUGA E., COSSU C. A note on the stability of slip channel flows[J]. Physics of Fluids, 2005, 17(8): 088106.

[6] MAKINDE O. D. On the Chebyshev collocation spectral approach to stability of fluid flow in a porous medium[J]. International Journal for Numerical Methods in Fluids, 2009, 59(7): 791-799.

[7] MAKINDE O. D., MOTSA S. S. Hydromagnetic stability of plane-Poiseuille flow using Chebyshev spectral collocation method[J]. Journal of Institute of Mathe-

[8] MAKINDE O. D., MHONE P. Y. Temporal stability of matics and Computer Sciences, 2001, 12(2): 175-183. small disturbances in MHD Jeffery-Hamel flows[J]. Computers and Mathematics with Applications, 2007, 53(1): 128-136.

[9] MAKINDE O. D., MHONE P. Y. On temporal stability analysis for hydromagnetic flow in a channel filled with a saturated porous medium[J]. Flow, Turbulence and Combustion, 2009, 83(1): 21-32.

[10] RUDRAIAH N., SHANKAR B. M. and NG C. O. Electrohydrodynamic stability of couple stress fluid flow in a channel occupied by a porous medium[J]. Special Topics and Reviews in Porous Media-An International Journal, 2011, 2(1): 11-22.

[11] COUTINHO J. E. A., De LEMOS M. J. S. Laminar flow with combustion in inert porous media[J]. International Communications in Heat and Mass Transfer, 2012, 39(7): 896-903.

[12] SUNDARAVADIVELU K., TSO C. P. Influence of viscosity variations on the forced convection flow through two types of heterogeneous porous media with isoflux boundary condition[J]. International Journal of Heat and Mass Transfer, 2003, 46(13): 2329-2339.

[13] VALDES-PARADA F. J., OCHOA-TAPIA J. A. and ALVAREZ-RAMIREZ J. On the effective viscosity for the Darcy-Brinkman equation[J]. Physica A-Statistical Mechanics and Its Applications, 2007, 385(1): 69-79.

[14] KRASNOV D. S., ZIENICKE E. and ZIKANOV O. et al. Numerical study of the instability of the Hartmann layer[J]. Journal of Fluid Mechanics, 2004, 504: 183-211.

[15] GOLUB G. H., Van Der VORST H. A. Eigenvalue computation in the 20th century[J]. Journal of Computational and Applied Mathematics, 2000, 123(1-2): 35-65.

10.1016/S1001-6058(14)60076-7

* Project supported by the Research Grants Council of the Hong Kong Special Administrative Region, China (Grant No. HKU 715510E).

Biography: SHANKAR B. M. (1985-), Male, Ph. D.,

Assistant Professor

NG Chiu-On,

E-mail: cong@hku.hk