程晓亮

(吉林师范大学 数学学院,吉林 四平 136000)

0 引言

在Poincaré1907年工作的基础上，S.Bochner，C.Fefferman，S.S.Chern-S.Ji，X.Huang-S.Ji 分别于1943年，1974年，1996年和1998年研究了Cn中域上的双全纯映照与其边界上的CR映照的等价性[1-3].从而，建立了研究单位球上的逆紧全纯映照问题与研究单位球面上的CR映照问题的桥梁.1977年,Alexander证明了多元复欧式空间Cn中的单位球Bn到Bn上的逆紧全纯映照F是Bn上的自同构，1979年，S.M.Webster证明了具有三次连续可微边界的Bn到Bn+1(n>2)的逆紧全纯映照一定是线性嵌入，1982年，J.Faran分类了具有连续可微边界的B2到B3上的有理逆紧全纯映照等价于Whitney映照或者另一简单映照[4-6].

20世纪90年代以来,X.Huang,S.Ji,J.P.D’Angelo等众多学者研究了一般的单位球Bn到BN上的逆紧全纯映照与单位球面上CR映照问题，对逆紧全纯单项式、多项式和有理映照进行了部分的分类，证明了B2到BN上的任意二次有理逆紧全纯映照必然等价于B2到B5上的二次有理逆紧全纯映照，证明了B2到BN上的二次有理逆紧全纯映照必然等价于B2到B5上的二次多项式逆紧全纯映照等一系列结果[7-15].在多元复分析中即使对较低维数的单位球间的逆紧全纯映照，写出其多项式映照的显示表达式也不是平凡的事.

1 B2到B4的逆紧全纯映照

设C为复数域，其n重笛卡尔积Cn={(z1,z2,…，zn)|zi∈C,i=1,2,…，n}在标准欧式度量下构成n维复欧式空间.

又Bn={(z1,z2,…，zn)||z1|2+|z2|2+…+|zn|2<1，(z1,z2,…,zn)∈Cn}为Cn中单位球.下面我们讨论的映照其定义域均为二维单位球B2={(z,w)||z|2+|w|2<1，(z,w)∈C2}，其目标空间为四维单位球B4={(z1，z2，z3,z4||z1|2+|z2|2+|z3|2+|z4|2<1，(z1,z2,z3,z4)∈C4}.

相应的单位球面记为

∂B2={(z,w)||z|2+|w|2=1,(z,w)∈C2}，

∂B4={(z1,z2,z3,z4)||z1|2+|z2|2+|z3|2+|z4|2=1，(z1,z2,z3,z4)∈C4}．

事实上，为了研究单位球间的逆紧全纯映照，Whitney， D′Angelo，J.Faran等构造了一些B2到B4上的逆紧全纯单项式映照的实例.

证明根据逆紧全纯映照的定义，只需验证该映照是∂B2到∂B4上的映照.

代入|z|2+|w|2=1，有

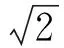
下面构造一族B2到B4上的逆紧全纯多项式映照，并加以证明.

2 定理及其证明

定理1设多项式族

f(z,w)=(g1,g2,g3,g4)，

则f(z,w)是B2到B4上的逆紧全纯多项式映照.

证明

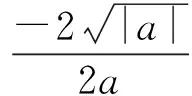
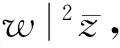
证毕.

[1]H.Jacobowitz.An introduction to CR structures[M].American Mathematical Society,Providence,Rhode Island,1990.

[2]S.Bochner.Analytic and meromorphic continuation by means of Green’s formula[J].Ann.of Math,1943 (2)：652～673.

[3]C.Fefferman.The Bergman kernel and biholomorphic mappings of pseudoconvex domains[J].Invent.Math,1974(6):1～65.

[4]H.Alexander.Proper holomorphic maps in Cn[J].Indiana Univ.Math.Journal,1977(4): 137～146.

[5]F.Forstneric.Proper holomorphic maps from balls[J].Duke Math.J,1986(2):427～441.

[6]J.Faran.Maps from the two ball to the three ball[J].Invent.Math,1982(3):441～475.

[7]X.Huang.On a linearity problem of proper holomorphic mappings between balls in complex spaces of different dimensions[J].J.Diff.Geom,1999(5):13～33.

[8]X.Huang,S.Ji.Mapping Bninto B2n-1[J].Invent Math,2001(2):219～250.

[9]J.P.D’Angelo.Proper holomorphic mappings between balls of different dimensions[J].Mich.Math.J,1988(1):83～90.

[10]J.P.D’Angelo.Polynomial proper holomorphic mappings between balls,II[J].Michigan Math.J,1991(1):53～65.

[11]Z.Chen,S.Ji,D.Xu.Rational proper holomorphic mappings from Bninto BNwith degree 2[J].Science in China: Series A Mathematics,2006 ,(11):1504～1522.

[12]S.Ji,Y.Zhang.Classification of rational proper holomorphic mappings from B2into BNwith degree 2[J].Science ChinaMathematics,2009， (12):2647～2667.

[13]J.Faran,X.Huang,S.Ji,Y.Zhang.Rational and polynomial maps between balls[J].Pure and applied Mathematics Quarterly,2010 (3):829～842.

[14]X.Cheng,S.Ji.Linearity and second fundamental forms for proper holomorphic maps from Bn+1to B4n-3[J].J.Geom.Anal，2012(4):977～1006.

[15]X.Cheng,S.Ji,W.Liu.CR Submanifolds in the Sphere and Their Gauss Maps[J].Science ChinaMathematics,2013(5):1041～1049.