吕海炜, 李映辉, 李中华, 李 亮

（1.西南交通大学 力学与工程学院，成都 610031；2.中国石油宝鸡石油机械有限责任公司，宝鸡 721002）

0 引言

物体由轴向运动诱发产生的横向振动[1-3]，对系统的振动频率和稳定性有很大影响，而且可能导致运动失稳。有研究表明，为了改善鸭式飞机（V-173）的横向稳定性，通常在其垂直尾翼下安装阻尼夹层板[3]。这是一个典型高速飞行黏弹性阻尼夹层板的例子，其他飞行夹层结构还有例如飞机蒙皮、航天器展开附件、高速飞行导弹外壳等。由轴向运动引起横向振动并导致失稳的问题有广泛背景，因此对超声速气流下黏弹性夹层壁板的颤振进行研究具有重要的工程应用价值。

壁板颤振问题研究始于20世纪50年代，学者们使用不同方法对该问题进行了研究。Dowell[4]对1970年以前学者们在壁板颤振分析中所做的工作进行了全面总结，主要包括使用的结构理论和气动力理论，同时还详细分析了上述各种理论的缺点并提出了相应的改进方法；Deman 和Dowell[5]基于二维不可压缩涡格气动力理论从理论及实验上研究了两端固支两端自由的二维壁板的极限环振动和线性颤振边界；Jinsoo 和Younhyuck[6]使用非定常三维面法研究了机翼的超声速颤振；Bogdan 等[7]基于von-Karmen 大变形理论和线性活塞理论，使用 有限差分法、Galerkin 法及正交分解法研究了非定常超声速气流下壁板的非线性振动；Plaut 等[8]研究了各态历经静态高斯随机载荷的长弹性板在超声速气流下的稳定性；Bismarck-Nasr 和Bones[9]使用摄动法得到固支平板的极限环振动解，研究了结构阻尼对非线性壁板颤振的迟滞影响；Beldica 等[10]作了大量关于黏弹性壁板颤振的研究，主要关注材料的性能和结构的蠕变寿命时间；Kiiko[11]使用B-G 法和平均法研究了黏弹性矩形板的动力稳定性及黏性系数对临界参数的影响；Gordnier 和Visbal[12]使用数值算法研究了非线性壁板颤振的三维黏弹性解；Kyo-Nam 和Woo-Seok[13]基于哈密顿原理及线性活塞理论得到了复合材料壁板的超声速颤振方程，研究了迟滞和气动阻尼对颤振的影响；Bolotin 等[14]研究了初始条件对非线性弹性壁板的后临界行为的影响，主要关注弹性壁板分叉边界和混沌吸引子；张云峰和刘占生[15]研究了黏弹性材料壁板在超声速来流作用下颤振时的分叉及混沌等复杂动力学特性；肖艳平等[16]基于Kelvin-voigt 黏弹性本构模型，根据von-Karmen 大应变-位移关系和一阶活塞气动力理论，建立了二维黏弹性壁板颤振方程，采用数值方法分析了黏弹性阻尼、面内压力及壁板几何尺寸对黏弹性壁板颤振的影响，并研究了黏弹性壁板颤振时的分叉及混沌特性；李映辉 等[17]基于薄板小变形理论和一阶气动力活塞理论建立了三维黏弹性夹层壁板的气动弹性颤振方程，并用Galerkin 截断方法研究了系统的不同参数对颤振特性的影响。

由上可见，研究超声速气流下弹性结构和黏弹性结构颤振方面的文献相当多，但对黏弹性阻尼夹层结构颤振研究较少。鉴于此，本文将研究超声速气流下黏弹性阻尼夹层结构的颤振特性。

1 黏弹性夹层板颤振方程

图1为超声速气流下黏弹性夹层板的模型，其几何尺寸和材料参数与实际的轴向运动黏弹性夹层板一致，不同的是夹层板上表面有沿x方向的超声速气流时，夹层板将会受气动力作用。

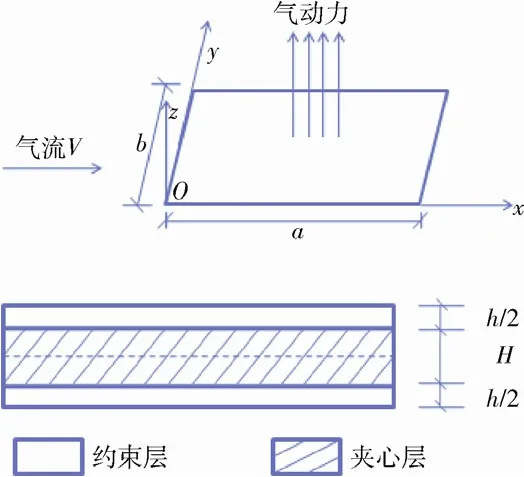
图1 黏弹性夹层壁板模型Fig.1 Model of the viscoelastic sandwich panel

在文献[17]中若考虑几何非线性，即黏弹性夹层板应变εx、εy、γxy与挠度w的关系为：

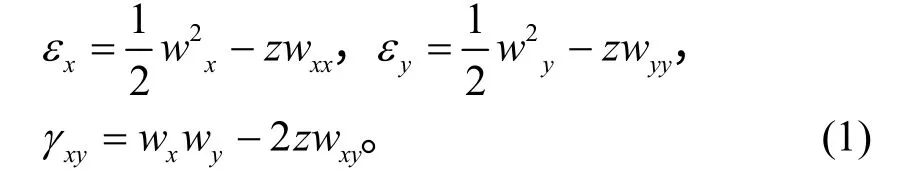
且超声速气流作用下产生的气动载荷p采用三阶活塞理论[18]可表示为

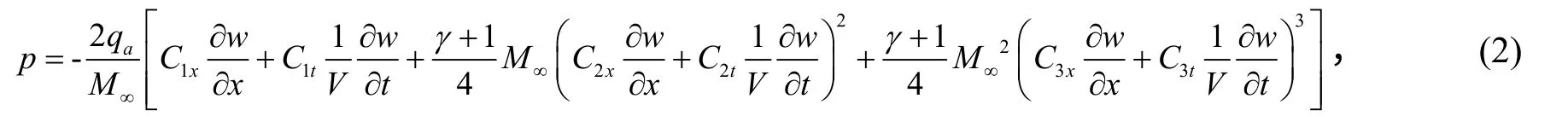
其中：qa=ρ∞V2/2 表示动压，ρ∞为来流空气密度；M∞为马赫数；V为来流速度；Cit和Cix(i=1, 2, 3)取0或1，就可分别讨论气动力相应子项对壁板气动弹性稳定性的影响。

则可得超声速气流下黏弹性夹层壁板颤振的非线性振动方程为

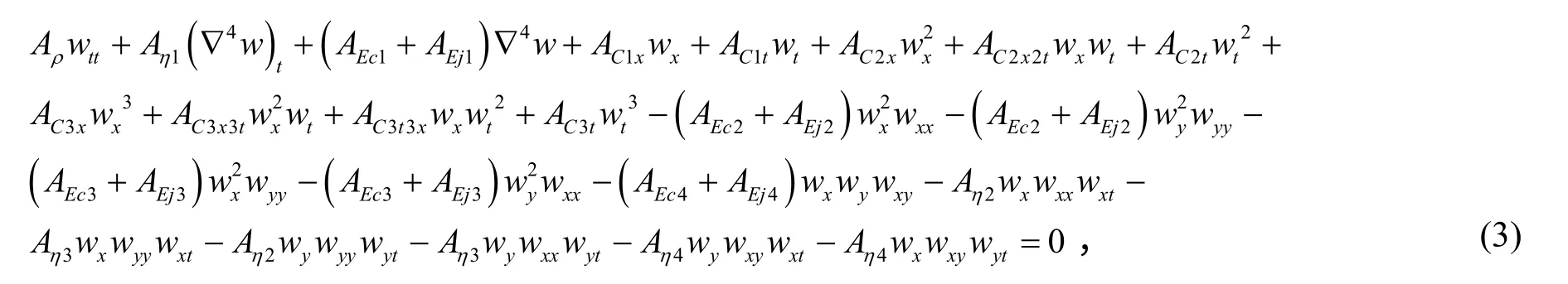
其系数见文后附录。

2 Galerkin 离散

对四边简支壁板，边界条件为

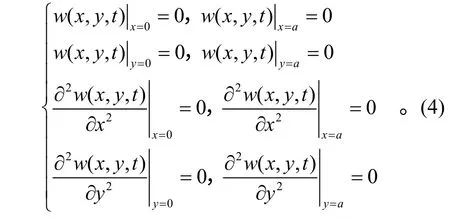
设方程(3)的解形式为

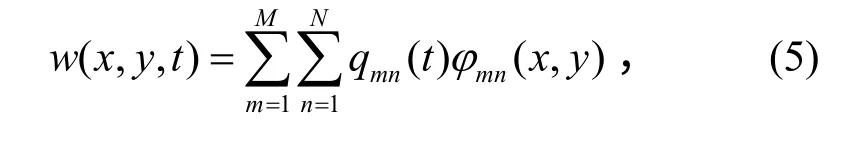
其中：φmn(x,y)是满足边界条件的试函数；M、N为 截断阶数。在四边简支条件下通常取

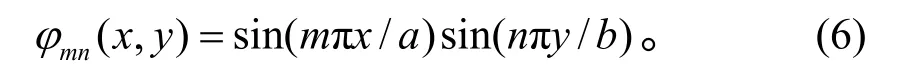
将式(5)代入方程(3)，得系统的残差R(x,y,t)（详见文献[19]）。使用Galerkin 方法，得

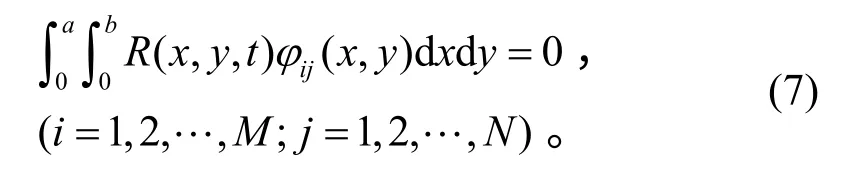
2.1 一阶非线性分析

2.1.1 一阶截断方程

由文献[18]可知，由于壁板的两边被简支，又与来流垂直，高阶模态不易被激发，在y方向的截断取一阶模态就可以体现此方向上变形的影响，故在垂直来流y方向上，N值取为1。

令M=1，得到一阶截断方程。令x1=q11，x2=，得到二维一阶常微分方程组：

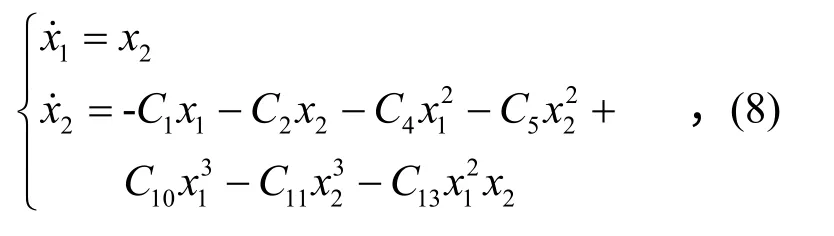
其系数见附录。

2.1.2 系统的平衡点及其稳定性 系统的平衡点为

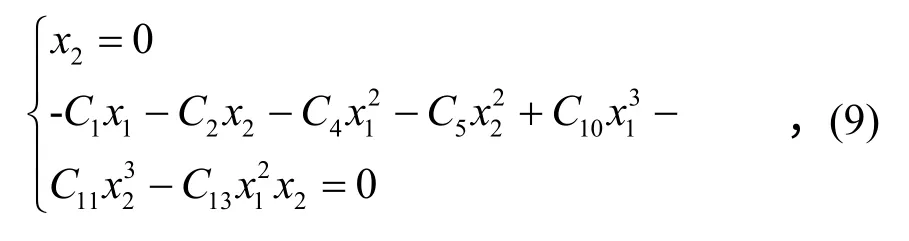
求得方程(8)有3 个平衡点，分别为：

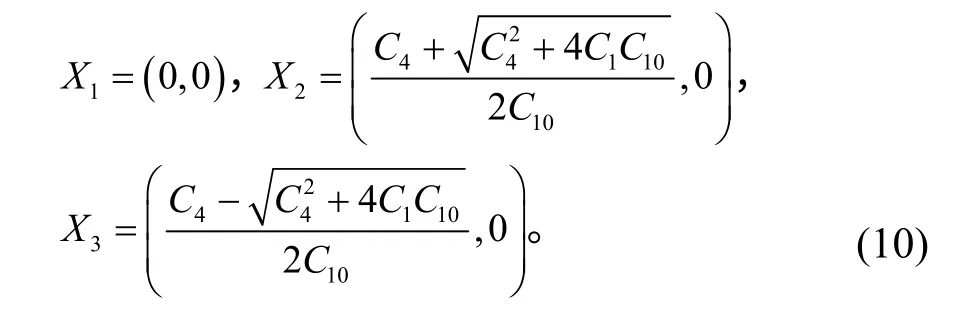
要使平衡点X2和X3有意义，须满足即来流速度应满足

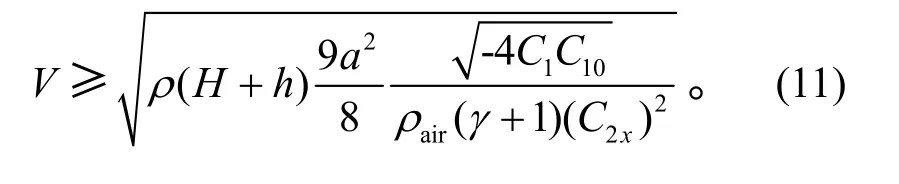
当来流速度超过此速度时，系统发生静态分叉，平衡点的个数将由1 个变为3 个。

式(8)的Jacobi 矩阵为

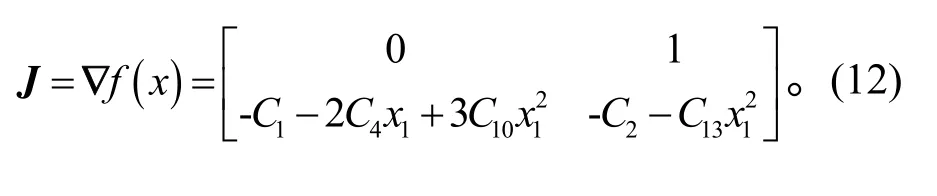
X1=(0,0)处的特征方程为

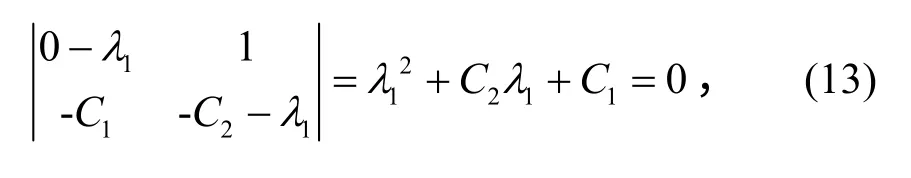
其中λ1为X1的特征根，求得

λ1=令C22- 4C1= 0，得系统的临界来流速度为

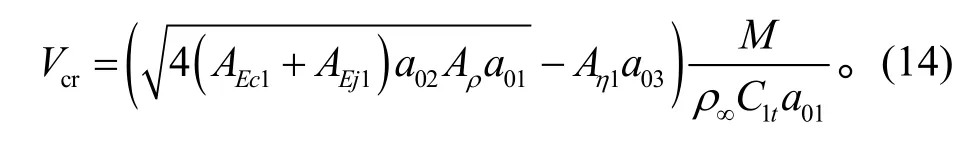
由C1＞0，C2＞0 可知该平衡点的两个特征根均具有负实部，所以是稳定的。

与讨论平衡点X1的计算方法一样，可计算平衡点X2、X3处Jacobi 矩阵的特征值，从而判断其稳定性。

2.1.3 数值模拟

超声速气流下黏弹性夹层壁板的几何参数见表1，材料参数见表2。气动力参数为：马赫数M∞=5，比热比γ=1.4，C1x=C1t=C2x=C2t=C3x=C3t=1。

表1 黏弹性夹层板几何参数Tabel 1 Geometrical size of viscoelastic sandwich panel

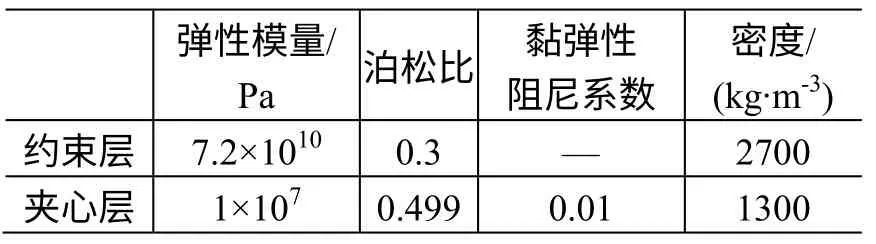
表2 黏弹性夹层板材料参数Tabel 2 Materials parameters of viscoelastic sandwich panel

图2给出了平衡点随来流速度变化的分叉图。从图2中可以看到，当速度小于7571 m/s 时，系统只有一个平衡点X1；当速度大于7571 m/s 时，系统的平衡点个数由1 个变为3 个。

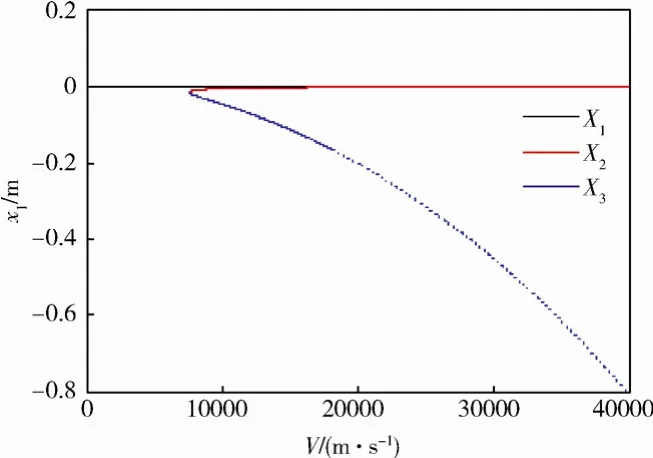
图2 平衡点随来流速度变化Fig.2 The equilibrium points against the flow speed

图3为平衡点X1的特征值λ1随来流速度变化情况。从图中看到，当来流速度小于27 036 m/s 时，随着来流速度的增加，特征值λ1的虚部绝对值逐渐减小，实部（始终为负）绝对值逐渐增大，故平衡点X1为稳定的焦点；当来流速度大于27 036 m/s时，特征值虚部为0，实部则分为两支，但数值均小于0，说明此时平衡点仍然是稳定的，只是平衡点类型由稳定的焦点变为稳定的结点。

图4为平衡点X2的特征值λ2随来流速度变化情况。从图中看到，特征值λ2虚部始终为0，且为一正一负，说明平衡点X2为不稳定的鞍点。

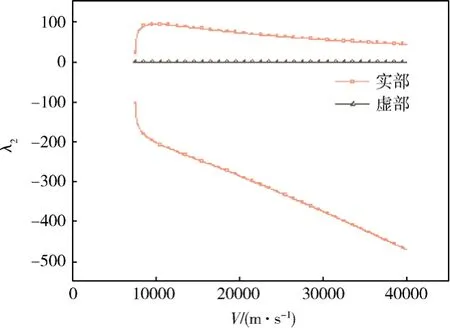
图4 特征值λ2 随来流速度变化Fig.4 The eigenvalue (λ2) against the flow speed

图5为特征值λ3随来流速度变化情况。因特征值λ3实部与虚部绝对值相差较大，在图5中不能完全反映λ3实部的真实走向，故单独画出其实部随来流速度变化图（图6）。从图5和图6看到，特征值λ3虚部绝对值随来流速度增大而增大，当来流速度在区间(7571, 18 161) m/s 中，实部为负数，平衡点X3为稳定的焦点；当来流速度等于18 161 m/s 时，实部等于0，特征值为纯虚数，此时平衡点X3为中心；当来流速度超过18 161m/s，特征值实部变为正数，并随来流速度的增大而增大，此时平衡点X3的类型为不稳定焦点。

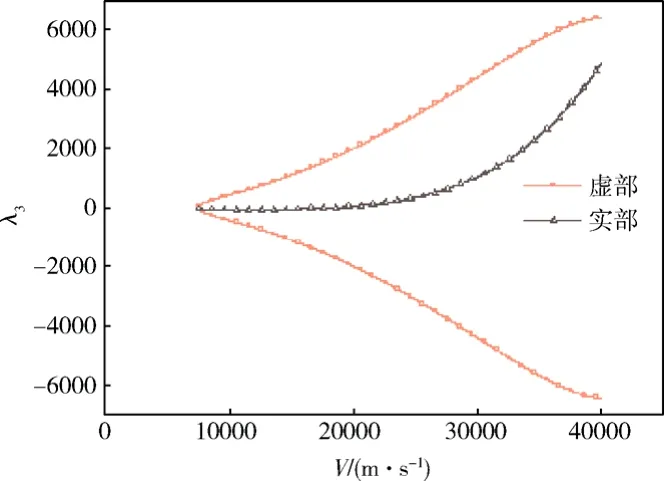
图5 特征值λ3 随来流速度变化Fig.5 The eigenvalue (λ3) against the flow speed

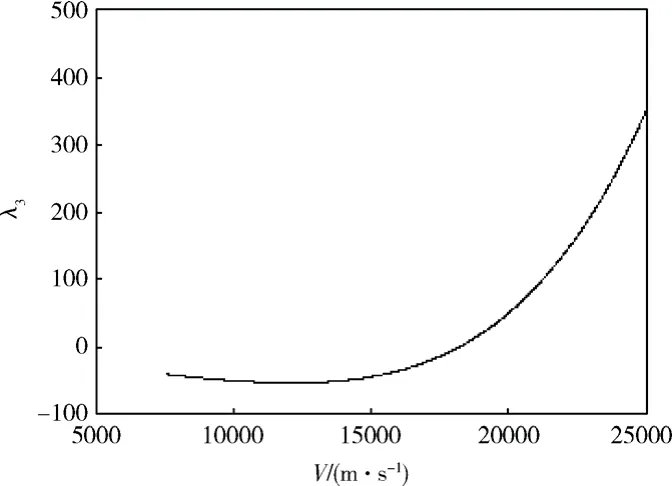
图6 特征值λ3 实部随来流速度变化Fig.6 The real part of eigenvalue (λ3) against the flow speed

表3给出了关键来流速度下平衡点的特征值及其平衡点类型。

表3 关键来流速度下平衡点的特征值及其类型Table 3 The eigenvalue at the equilibrium point and its type under typical flow speeds

2.2 二阶非线性分析

2.2.1 二阶截断方程

令M=2，得二阶截断方程组。令则有

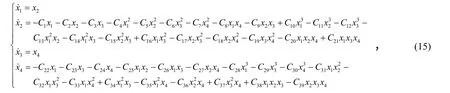
其中相关系数C1，C2，．．．，C39见文后附录。将式(15)写为矢量形式为=f(x)，x∈R4。

2.2.2 系统发生Hopf 分叉的临界来流速度

由f(x)=0，即可求得系统的平衡点。显然X0= [0，0，0，0]是系统的平衡点。在X0处的Jacobi矩阵为

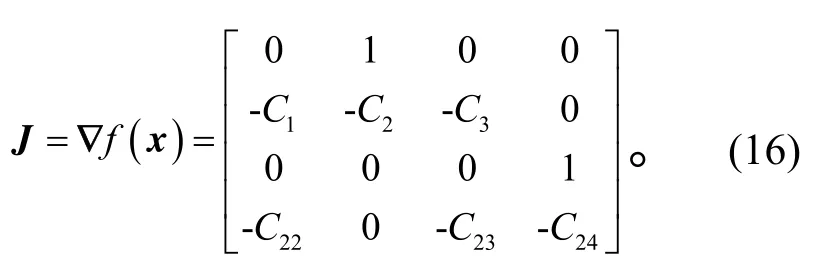
由分叉理论，考虑式(16)的特征值可得发生分叉的边界曲线方程，则其特征方程为

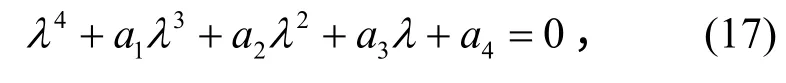
其中：

由于马赫数M∞、来流速度、黏弹性系数大于0，可知a1＞0，a2＞0，a3＞0，a4＞0。式(18)的Hurwitz行列式为

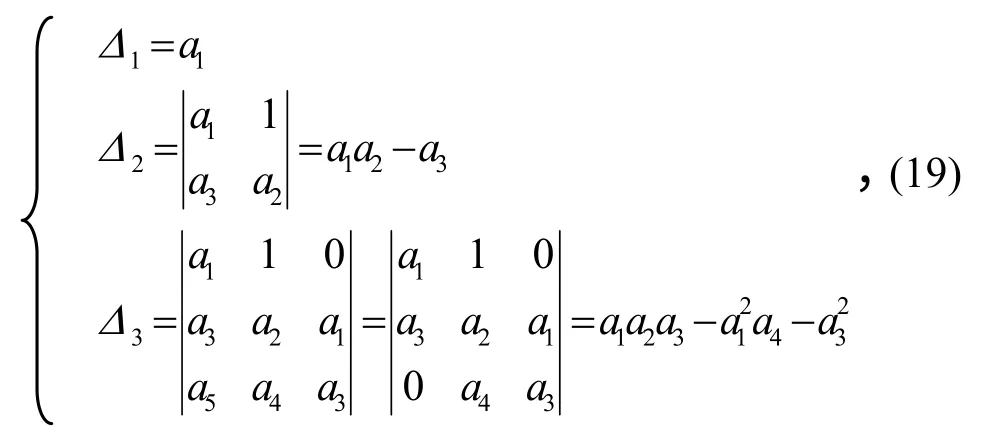
其中Δ1＞0，Δ2＞0，令Δ3=0，可解出临界来流速度Vcr。

2.2.3 数值模拟

2.2.3.1 平衡点的稳定性

非零平衡点的稳定性也可通过上述方法判断，因f(x)为高阶非线性方程组，无法求其解析解，本文通过数值方法求其数值解。所使用的几何参数见表1，材料参数见表2。

图7给出了在平衡点X0处Δ3随来流速度变化图。数值分析结果表明，随着来流速度的变化，系统始终只有平衡点X0。可以看到当来流速度为1700 m/s时，Δ3=0。当来流速度未达到临界来流速度时，Δ3＞0，根据Hurwitz 定理判断在此区间的平衡点X0是稳定的焦点；当来流速度为1700 m/s 时，Δ3=0，此时平衡点为稳定极限环；超过临界速度后Δ3＜0，平衡点变为不稳定焦点。表4给出了关键来流速度 下平衡点X0处Jacobi 矩阵的特征值。

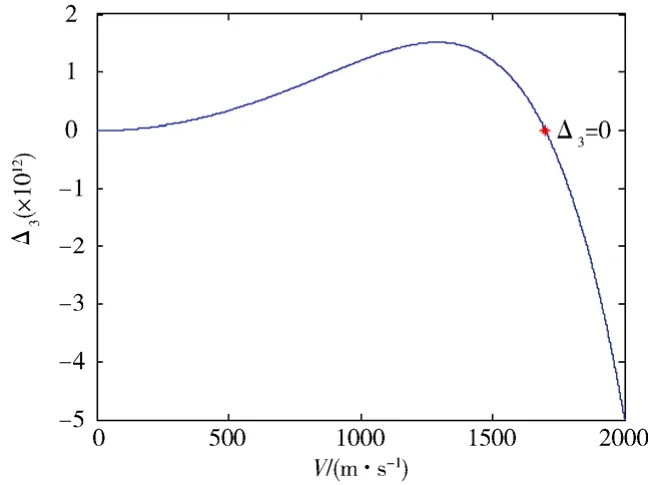
图7 Δ3 随来流速度变化Fig.7 Δ3 against the flow speed

表4 关键来流速度下平衡点X0 特征值及类型Table 4 The eigenvalue at X0 and its stability under different flow speeds

2.2.3.2 Hopf 分叉图

图8给出了二阶截断下系统随来流速度变化的Hopf 分叉图，其中图8(b)为来流速度在[1600, 2000]m/s 区域的分叉图。

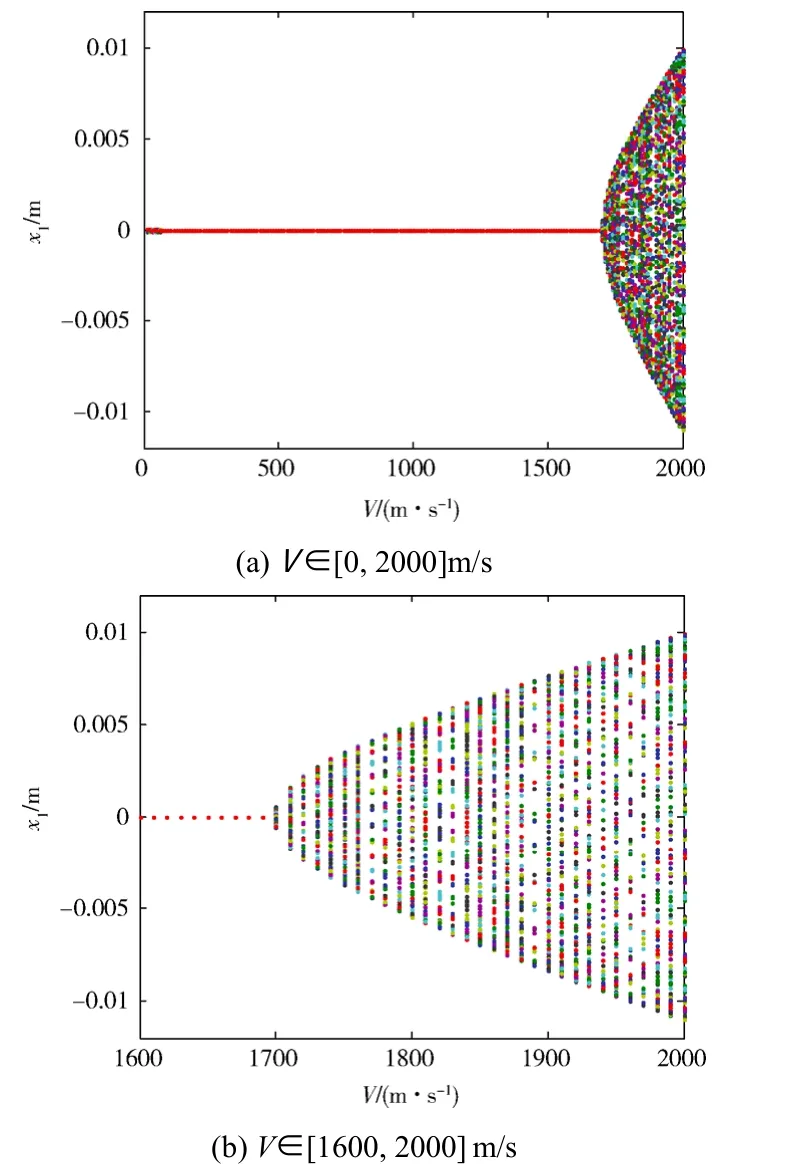
图8 二阶截断下系统随来流速度分叉图Fig.8 Bifurcation diagram under the second order truncation

2.2.3.3 不同来流速度下系统的时间历程图和 相图

当V＜1700 m/s 时，系统仅有稳定的平衡点X0，不论初值大小，最后都趋于此平衡点。图9、图10给出了二阶截断下来流速度V＝1500 m/s、1690 m/s，初值取(0.000 01, 0.01, 0.000 01, 0.01)时系统的时间历程图和相图。可以看到系统作衰减运动，说明系统是稳定的。

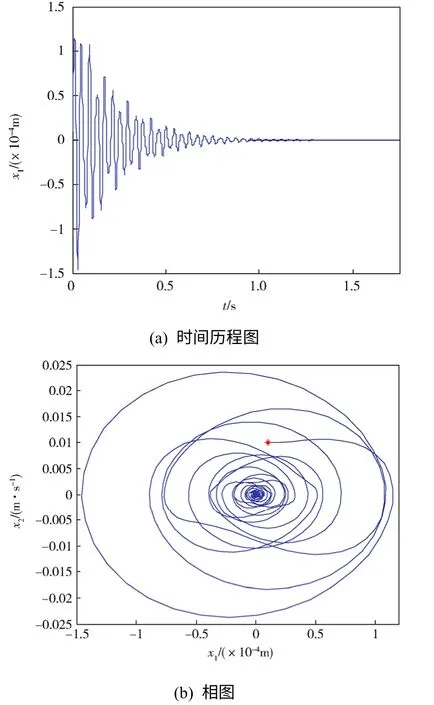
图9 二阶截断下来流速度V=1500 m/s 时系统时间 历程图和相图 （其中红色*号表示初始点，绿色+号表示终结点，下同）Fig.9 The time history and phase portrait of the system when V=1500 m/s

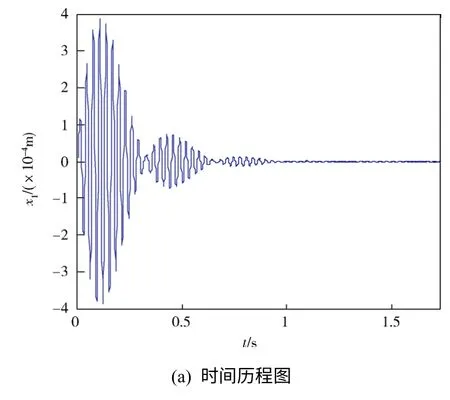
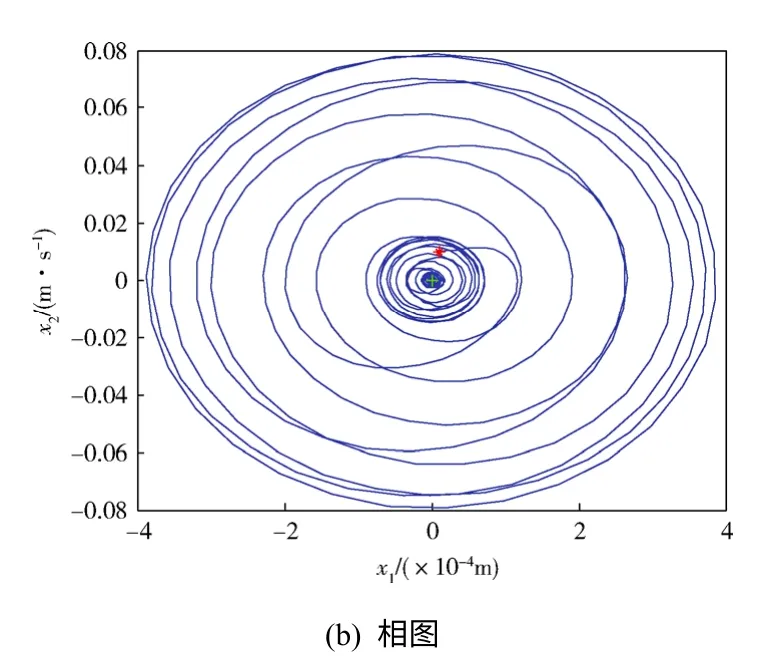
图10 二阶截断下来流速度V=1690 m/s 时系统时间 历程图和相图Fig.10 The time history and phase portrait of the system when V=1690 m/s

当V≥1700 m/s时，平衡点X0变得不稳定；但由于发生Hopf分叉产生稳定的极限环，轨线均趋于稳定的极限环。图11、图12分别给出了来流速度V=1700 m/s、2000 m/s，初值为(0.000 01, 0.01, 0.000 01, 0.01)时系统的时间历程图，可以看出，当速度大于等于 1700 m/s时，系统作周期运动。

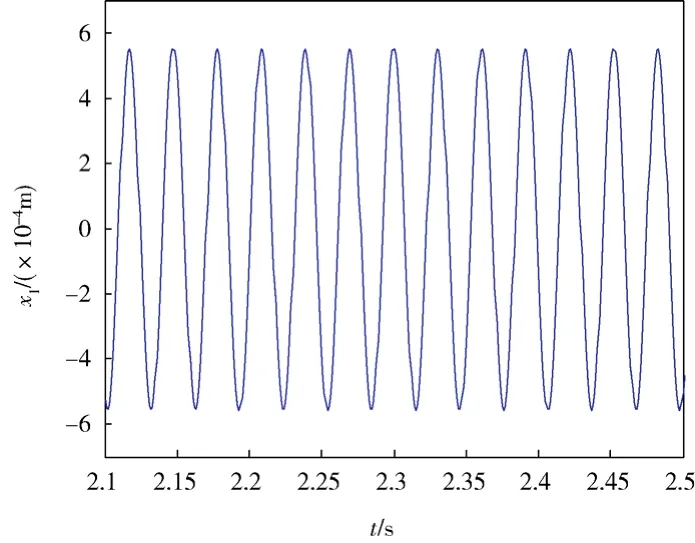
图11 二阶截断下来流速度V=1700 m/s 时系统时间历程图Fig.11 The time history of the system when V=1700 m/s

图12 二阶截断下来流速度V=2000 m/s 系统时间历程图Fig.12 The time history of the system when V=2000 m/s

3 结束语

本文基于von-Karmen 薄板大挠度理论、Kelvin-Voigt 黏弹性本构方程和非线性活塞理论，建立了超声速黏弹性夹层板颤振非线性方程，并使用Galerkin 方法研究该方程。对非线性系统主要研究了随着来流速度的变化，系统的平衡点及稳定性变化情况，得到如下结论：

1）对于一阶截断，系统在来流速度小于临界来流速度7571 m/s 时只有一个平衡点，且平衡点类型为稳定焦点；当来流速度超过临界来流速度后，系统的平衡点个数，由1 个变为3 个。平衡点X2始终为不稳定的鞍点；平衡点X3在来流速度 18 161 m/s 处稳定性发生改变，由稳定的焦点变为不稳定焦点。

2）对于二阶截断，得到系统发生Hopf 分叉时的临界速度为1700 m/s。使用数值方法研究了黏弹性夹层壁板随来流速度变化的动力学行为：来流速度在临界速度前，系统作稳定的衰减运动；临界速度后，系统产生周期运动。

研究表明，对同一系统采用不同的截断，得到的临界速度差别相当大。应该说，所取的截断阶数越高，得到的结果越符合实际。

（References）

[1]Mote C D Jr.A study of band saw vibration[J].Journal of the Franklin Institute, 1965, 279(6)∶430-444

[2]Mote C D Jr.Dynamic stability of axially moving band[J].Journal of the Franklin Institue, 1968, 285(5)∶329-346

[3]Eun H B, Hwang M S, Park W J, et al.Lateral stability verification of a canard air plane with and without a vertical panel[J].Transactions of Nanjing University of Aeronautics and Astronautics, 2003, 20(2)∶125-133

[4]Dowell E H.Panel flutter∶a review of the aeroelastic stability of plates and shells[J].AIAA Journal, 1970, 8(3)∶385-399

[5]Deman T, Dowell E H.Limit cycle oscillations of two-dimensional panels in low subsonic flow[J].International Journal of Non-Linear Mechanics, 2002, 37(7)∶1199-1209

[6]Jinsoo C, Younhyuck C.Supersonic flutter analysis of wings using an unsteady 3D panel method[J].Computers and Fluids, 2001, 30(2)∶237-256

[7]Bogdan I E, Liaosha S T, Michael P P.Coherent structures and their influence on the dynamics of aeroelastic panel[J].International Journal of Non-Linear Mechanics, 2004, 39(6)∶977-991

[8]Plaut R H, Infante E F.On the stability of continuous systems subjected to random excitations[J].Journal of Applied Mechanics, 1970, 37(3)∶623-628

[9]Bismarck-Nasr M N, Bones C A.Damping effects in nonlinear panel flutter[J].AIAA Journal, 2000, 38(4)∶711-713

[10]Beldica C E, Hilton H H, Kubair D.Viscoelastic panel flutter-stability, probabilities of failure and survival times[C]//Proceedings of the 42ndAIAA/ASME/ASCE/ AHS/ASC Structures, Structural Dynamics and Materials Conference.Seattle, WA, USA, 2001∶3423-3433

[11]Kiiko A.Flutter of a viscoelastic plate[J].Journal of Application Mathematics and Mechanics, 1996, 60(1)∶167-170

[12]Gordnier R E, Visbal M R.Development of three- dimensional viscous aeroelastic solver nonlinear panel flutter[J].Journal of Fluids and Structures, 2002, 16(4)∶497-527

[13]Kyo-Nam K, Woo-Seok H．Effects of hysteretic and aerodynamic damping on supersonic panel flutter of composite plates[J]．Journal of Sound and Vibration, 2004, 273(3)∶569-583

[14]Bolotin V V, Grishko A A, Kounadis A N, et al.Influence of initial conditions on the post-critical behavior of a nonlinear aeroelastic system[J].Nonlinear Dynamics, 1998, 15(1)∶63-81

[15]张云峰, 刘占生.粘弹壁板颤振的非线性动力特性[J].推进技术, 2007, 28(1)∶103-107 Zhang Yunfeng, Liu Zhansheng.Nonlinear dynamic analysis of viscoelastic panel flutter[J].Journal of Propulsion Technology, 2007, 28(1)∶103-107

[16]肖艳平, 杨翊仁, 叶献辉.三维粘弹壁板颤振分析[J].振动与冲击, 2011, 30(1)∶82-86 Xiao Yanping, Yang Yiren,Ye Xianhui.Flutter analysis for a three-dimensional viscoelastic panel[J].Journal of Vibration and Shock, 2011, 30(1)∶82-86

[17]李映辉, 李中华.超声速下粘弹性夹层壁板颤振分析[J].力学季刊, 2012, 33(3)∶449-455 Li Yinghui, Li Zhonghua.Flutteranalysis of viscoelastic sandwich panel under supersonic speed[J].Chinese Quarterly of Mechanics, 2012, 33(3)∶449-455

[18]叶献辉.壁板非线性气动弹性颤振及稳定性研究[D].成都∶西南交通大学博士学位论文, 2008

[19]李中华.轴向运动黏弹性夹层板振动分析[D].成都∶西南交通大学硕士学位论文, 2012

附 录

且