一维具有次近邻相互作用海森堡链中的量子关联
2013-10-28黄军林章青袍黄瑶瑶范楚辉
黄军林,章青袍,黄瑶瑶,范楚辉,孙 哲
(杭州师范大学理学院,浙江 杭州 310036)
一维具有次近邻相互作用海森堡链中的量子关联
黄军林,章青袍,黄瑶瑶,范楚辉,孙 哲
(杭州师范大学理学院,浙江 杭州 310036)
运用Quantum discord(QD)的概念,研究了一维带有次近邻相互作用的自旋1/2海森堡链中的量子关联特性.根据该系统的SU(2)以及Z2对称性,其约化密度矩阵具有简单的“X”型,从而解析得到QD的几何度量(GMQD)的表达式,并发现GMQD与两格点关联函数的关系,进而获得GMQD与能量本征值的关系.对于4格点和6格点情况,研究得到GMQD对于系统参数的依赖关系.通过数值和解析结果,发现GMQD在有限系统体系内是探测一级相变和无穷级相变的十分有效的工具.
量子失协;几何度量;量子相变;海森堡自旋链
0 引 言
作为量子信息与量子计算的核心概念,量子关联是目前最受关注的研究课题之一.通常,人们都认为量子计算器件的计算能力来源于量子纠缠——量子力学中最重要的非经典特性;但是最近,人们发现在量子纠缠之外,还存在着另外的非经典关联——Quantum discord(QD),其定义为总的互信息与经典互信息之间的差值[1].已有研究发现,QD能够提供更为丰富的具有非经典关联的量子态,例如,一些可分离态的QD并不等于零[2-3].事实上,只有QD为零才是经典关联的充要条件[4],所以,那些具有非零QD的态对于量子计算机而言,都是有价值的[5].因此,QD完全可能成为一种新的量子计算源——并且相较于量子纠缠更容易制备,在实验室内更易保存.
最近,人们对QD的研究热情越来越高[6-11].但是,即使有着种种优点,对QD的研究仍存在着一个很大困难——很难对其进行解析计算.甚至于对两比特系统,也仅仅只有诸如“X”态[12]等极少类型能够得到解析结果.源于此,Dakic等研究了两格点系统存在非零QD的充要条件,并提出了适用于任意两比特系统的QD的几何度量(GMQD)的概念[9].GMQD的提出大大简化了对QD的计算.
在量子多体关联系统中量子相变是一种非常重要而奇特的现象.作为一种量子临界现象,量子相变发生在绝对零度的条件下——此时,热涨落完全消失,从而不会有热力学相变发生.因此,量子相变是仅仅由系统参数的改变——诸如一个外加磁场,或耦合常数的改变——而引起的量子涨落.量子相变反映了系统基态结构的变化,因此,很容易意识到,那些与系统基态以及系统本征态密切相关的量子概念完全可能用来侦测量子相变的发生.
同样是一种量子关联,我们很自然地考虑QD与量子相变之间的联系.最近,人们开始利用QD的概念来研究探测QPT.有研究表明,在有限温度下,QD在量子临界点附近也有特殊的行为[13].而另一方面,环境中的量子临界性对于QD的动力学演化也有着重要影响[4,14].在部分量子相变的典型模型中,人们发现,经典关联与量子关联均对量子相变有所反映[15].所有的这些都说明,QD对于探测量子相变而言,是一种有效的工具.
本文将利用QD研究一维具有次近邻相互作用的自旋1/2海森堡链的量子相变.该模型是一种存在相互作用竞争的多体模型,对诸如CuGeO3的一类材料的结构有着很好的描述[16].该模型有两个重要的量子相变过程[17-19]:一级相变和无穷级相变.一级相变发生在基态能级的交叉点,而无穷级相变则与第一激发态能级交叉有密切关系,可由第一激发态保真度来进行探测[20].但是,对于该系统量子关联特性还少有研究,所以本文将研究该系统基态及第一激发态的QD和GMQD,并利用其对量子相变进行探测.
1 Quantum Discord及其几何度量
1.1 Quantum Discord

在经典情况下,很显然,二者是相等的.然而,对于量子情况,则又不同.量子信息学中,用Von Neumann熵取代了经典情况下的Shannon熵,即H(S)=H(ρS)=-TrSρSlogρS,那么,I(S:A)=H(S)+H(A)-H(S,A),描述了系统S与仪器A之间的所有关联,包括经典关联与量子关联.而另一种定义J(X:Y)=H(X)-H(X|Y)则与经典情况有所区别.因为基于量子力学理论,如果S与A有量子关联,那么我们对A的测量将会导致态的坍缩,从而破坏这种关联性.所以,该定义得到的结果只能是经典关联而非量子关联.Harold Ollivier等定义了QD:

(1)

1.2QD的几何度量
由于QD的定义中存在着最优测量的问题,使其解析计算变得十分复杂与繁琐,甚至是不可能.目前也仅对于少数特殊形式的状态能够得到解析结果,包括Werner态、Bell态及X态等.而对于高维度甚至大多数2×2系统而言,都是很难得到解析结果的.为了解决这一问题,2010年,Borivoje Dakic等提出了QD的几何度量[9],即所需的态与所有QD为零的态之间的最小距离:Dg(ρ)=min||ρ-χ||2,其中,χ代表所有QD为零的态,对于两比特系统,可以表示为χ=p1|ψ1〉〈ψ1|⊗ρ1+p2|ψ2〉〈ψ2|⊗ρ2,其中|ψ1〉和|ψ2〉是两个正交态.由于任意的一个两比特密度矩阵都可以利用所谓的布洛赫基矢展开,表示为
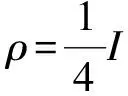
(2)
其中系数矩阵:
xi=Tr(σi⊗Iρ),yi=Tr(ρI⊗σi),
(3)
Tij=Tr(ρσi⊗σj),
(4)
其中:I为单位矩阵,σi是泡利矩阵.那么将密度矩阵ρ和χ都表示为布洛赫形式之后,代入GMQD的定义式,就得到

(5)

2 具有次近邻相互作用的一维海森堡链的GMQD
次近邻相互作用的一维海森堡链的哈密顿量为
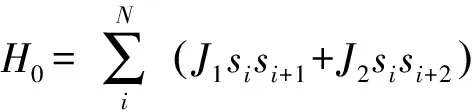
(6)
其中:N表示总格点数,下标i表示第i个格点,s为自旋算符,包括Sx,Sy,Sz3个分量,分别用泡利矩阵表示,J1,J2分别代表近邻及次近邻相互作用系数.选取周期性边界条件.对于本模型,仅仅在J2/J1=0及J2/J1=1/2时能够得到精确的解析解.同时,该模型存在两个重要的相变点:一级相变点Jc1=0.5及无穷级相变点Jc2≈0.241,(JC=J2/J1).在Jc1=0.5处,系统为Majumdar-Ghosh模型,此时系统基态的耦合自旋为零,是简并的,可以看作由最近邻两格点间的自旋单态等概率叠加而成(对于偶数格点以及无穷格点情况满足上述讨论).该点是基态能级交叉点,是由平移不变性破缺引起的,因此为一级相变点.

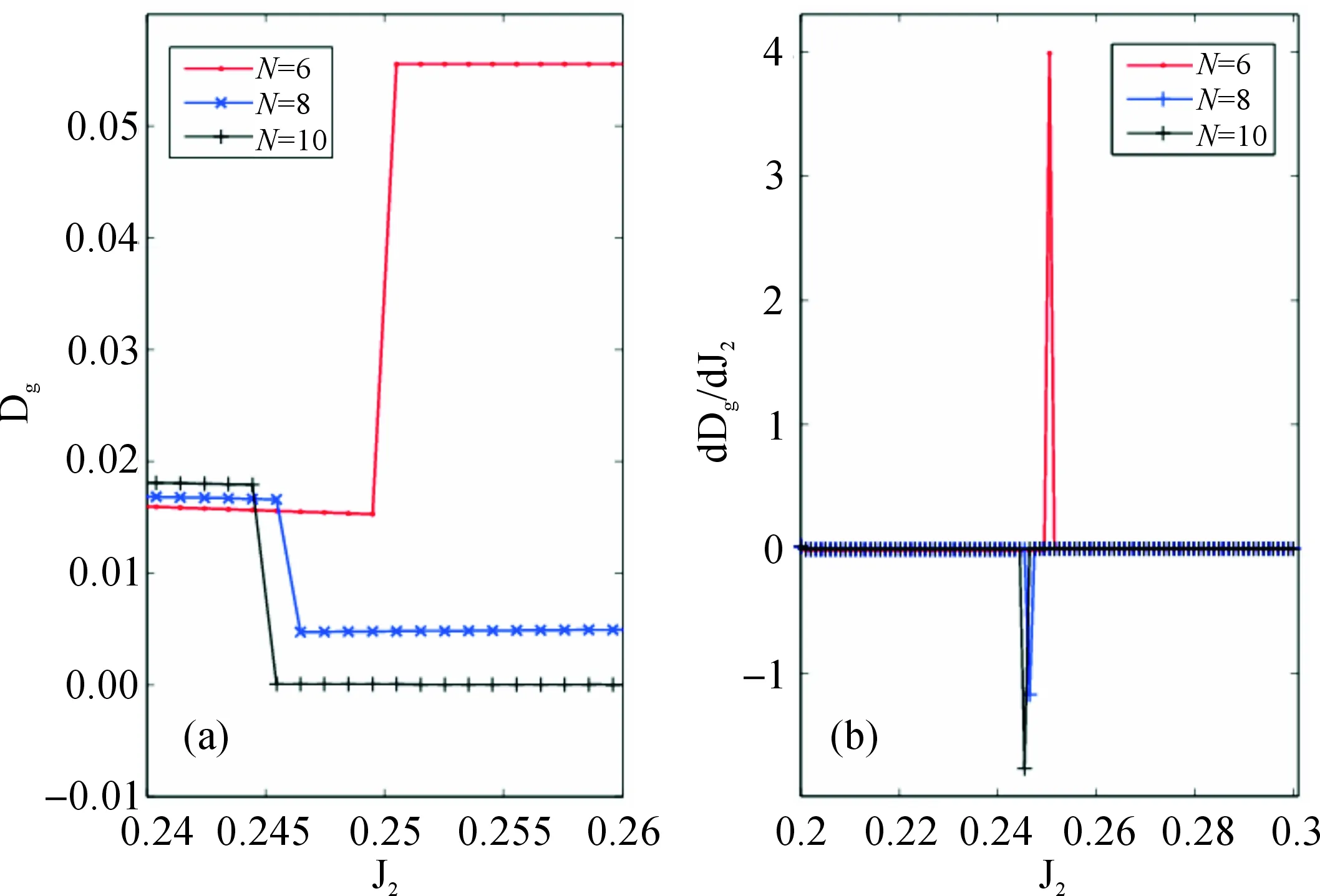
图1 自旋-1/2次近邻相互作用海森堡模型不同格点数的低能级能谱图Fig. 1 Low-level energy spectrum of the spin-1/2 Heisenberg chain with NNN interaction for different system sizes N=4,6,8,10.
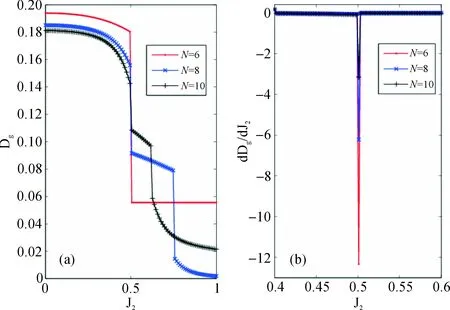
而在Jc2≈0.241处,系统将发生Berezinskii-Kosterlitz-Thouless(BKT)型相变,即自旋由流体序转向二聚序.这种相变是由最近邻相互作用及次近邻相互作用之间的竞争所导致的:当J2/J1 图1给出了不同格点数系统随J2参数变化的低能级图(此处均默认J1=1).很显然,对于不同的格点数N=4、6、8、10,基态能级均在J2=0.5处发生了交叉,这与已知的一级量子相变点是精确对应的.而第一激发态能级随着格点数的增加,能级交叉点逐渐由J2≈0.26左移到J2≈0.244.由此可以预见当系统格点数增加至无限时,系统第一激发态能级交叉点将趋近于BKT相变点J2≈0.241.由此可见,系统的量子相变与系统能级结构的根本性变化是密切相关的,从而相关的量子本征态在量子相变点将呈现出特别的量子特性. (7) (8) (9) 将其代入式(5),得到 (10) 其中,k1=4(a-b)2,k2=k3=4c2,故 (11) (12) (13) 该公式适用于具有与J1-J2模型相同对称性的海森堡系统的一般情况,例如XXX型及二聚型海森堡链. 将以上结果代入式(12),可以得到最近邻格点约化密度矩阵元 (14) 与次近邻格点约化密度矩阵元 (15) 分别将式(14)、(15)代入到式(11)中,就得到最近邻格点的GMQD与系统内能的关系式 (16) 以及次近邻格点的GMQD与系统内能的关系式 (17) 以上的结果可以理解为:由于系统的GMQD直接依赖于密度矩阵的矩阵元,因此,GMQD的奇异行为也是由密度矩阵的矩阵元所引起的.而当系统发生量子相变时,系统基态的变化将引起密度矩阵的变化,从而导致GMQD的奇异行为.而通过费曼-海尔曼法则得到的GMQD与系统内能之间的关系可以发现,在临界点附近能量的不连续行为,也将在GMQD的变化中得到体现.而作为量子相变的有力判别工具之一的系统能量,与系统的GMQD是有密切联系的.上述结论不仅适用于基态情况,对于低激发态的情况也是适用的. 3.1 四格点情况的解析计算 由于边界条件的存在,系统的哈密顿量具有平移不变性,所以有[H,T]=0,其中,T为平移算符[21],定义为T|ψ1…ψm〉=|ψmψ1…ψm-1〉.因为[H,Jz]=0,因此利用上述平移算符,就可以将4格点情况下的16维Hilbert空间分成几个子空间,分别对应相同自旋翻转数,从而将其约化为低维度的矩阵,可以解析处理问题. (18) 对于这样一个2维矩阵,很容易得到它的本征值:E1=J2+1,E2=J2-2,E3=J2-1,E4=-3J2,E5=-J2.综合以上结果,可以得到基态能量:当J2≤0.5时,Eg=-2+J2;当J2≥0.5时,Eg=-3J2.第一激发态能量为:当J2≤0.25时,E1st=-1+J2;当0.25≤J2≤0.5时,E1st=-3J2;当J2≥0.5时,E1st=-2+J2.将基态能量与第一激发态能量分别代入GMQD与系统内能关系式(16),就得到系统GMQD的解析结果,对于基态有 (19) 而对于第一激发态有 (20) 显然,基态情况下,系统的GMQD在0.5左右是不连续的,而对于第一激发态情况,则有2个不连续点:0.25及0.5.这与已知的系统量子临界点有一定的对应性. 3.2 六格点情况的解析计算 (21) 当0.25≤J2<0.5时, (22) 当J2≥0.5时, (23) 显然,在J2=0.25及J2=0.5两个点左右,系统的第一激发态能量发生了突变,GMQD在该点也体现出了不连续的特性,如图2-图4所示. 图2 自旋-1/2次近邻相互作用海森堡模型不同格点数的基态最近邻格点GMQD图(右侧为其导数)Fig. 2 NN-site GMQD of the ground state versus coupling for different system sizes N= 6, 8, 10 图3 自旋-1/2格点次近邻相互作用海森堡模型不同格点数的第一激发态最近邻格点GMQD图(右侧为其导数)Fig. 3 NN-site GMQD of the first excited states versus coupling J2 for different system sizes N= 6, 8, 10 图4 自旋-1/2格点次近邻相互作用海森堡模型不同格点数的第一激发态次近邻格点GMQD图(右侧为其导数)Fig. 4 NNN-site GMQD of the first excited states versus coupling J2 for different system sizes N= 6, 8, 10 从以上数值计算结果中可以看到:对于基态情况,GMQD的突变点均在J2=0.5处,从图2右侧的导数图可以更清晰地看到一个尖峰,这意味着该点处GMQD的不连续性;而对于第一激发态而言,随着格点数的增加,GMQD的突变点逐渐向左移动,意味着当格点数增加至无穷大时,GMQD的突变点将趋近于J2=0.241.从图3、图4右侧的导数图可以更清晰地看到尖峰的移动,随着格点数越来越多,移动的幅度越来越小.次近邻GMQD与最近邻GMQD的不同之处只是在于,6格点情况GMQD有突然增大现象,而8、10格点情况有突然减小现象.在J2=0.241这一点,系统将发生著名的Berezinskii-Kosterlitz-Thouless(BKT)型相变,即自旋由流体序转向二聚序.这种相变是由最近邻相互作用及次近邻相互作用之间的竞争所导致的:当J2 运用GMQD研究了一维带有次近邻相互作用的自旋1/2海森堡链中基态以及第一激发态的量子关联特性.由于该系统具有SU(2)以及Z2对称性,可以解析得到GMQD与两格点关联函数的关系,进而得到GMQD与能量本征值的关系. 对于4格点情况和6格点情况,通过获得基态和第一激发态本征能量的解析结果,得到GMQD依赖于系统参数的解析结果,从中可以精确反映出第一个临界点位置Jc1=0.5.并且通过数值方法研究第一激发态的最近邻和次近邻格点的GMQD,发现当系统从6格点增加到10格点的过程中,GMQD的突变点逐渐趋近于第二个量子相变点Jc2≈0.241. 需要强调的是,虽然二体QD(或GMQD)的方法仅仅在有限尺度系统中有效,但这对于一般的理论和实验研究中仍然具有实际意义.利用QD(或GMQD)研究其他类型量子相变的系统中的量子关联问题是值得大家继续探索的. [1] Ollivier H ,Zurek W H. Quantum discord: a measure of the quantumness of correlations[J]. Phys Rev Lett, 2001,88(1):1-4. [2] Henderson L, Vedral V. Classical quantum and total correlations[J].J Phys A, 2001,34(25):6899-6905. [3] Luo Shunlong. Quantum discord for two-qubit systems[J]. Phys Rev A, 2008,77(4):1-6. [4] Liu Benqiong, Shao Bin, Zou Jian. Quantum discord for a central two-qubit system coupled to anXY-spin-chain environment[J]. Phys Rev A,2010,82(6):1-7. [5] Datta A ,Vidal G. Role of entanglement and correlations in mixed-state quantum computation[J]. Phys Rev A,2007,75(4):1-5. [6] Cen Lixiang, Li Xinqi, Shao Jiushu,etal. Quantifying quantum discord and entanglement of formation via unified purifications[J]. Phys Rev A,2011,83(5):1-4. [7] Li Bo, Wang Zhixi, Fei Shaoming. Quantum discord and geometry for a class of two-qubit states[J]. Phys Rev A,2011,83(2):1-5. [8] Li Zhenni, Jin Jiasen, Yu Changshui. Probing quantum entanglement, quantum discord, classical correlation, and the quantum state without disturbing them[J].Phys Rev A,2011,83(1):1-5. [9] Daki B, Vedral V, Brukner C. Necessary and sufficient condition for nonzero quantum discord[J]. Phys Rev Lett,2010,105(19):1-4. [10] Rulli C C ,Sarandy M S. Global quantum discord in multipartite systems[J]. Phys Rev A,2011,84(4):1-6. [11] Ali M, Rau A R P, Alber G. Quantum discord for two-qubitXstates[J]. Phys Rev A,2010,81(4):1-7. [12] Chen Qing, Zhang Chengjie, Yu Sixia,etal. Quantum discord of two-qubitXstates[J]. Phys Rev A,2011,84(4):1-5. [13] Werlang T, Ribeiro G A P, Rigolin G. Spotlighting quantum critical points via quantum correlations at finite temperatures[J]. Phys Rev A,2011,83(6):1-16. [14] Sun Zhe, Lu Xiaoming,Song Lijun. Quantum discord induced by a spin chain with quantum phase transition[J]. J Phys B,2010,43(21):1-8. [15] Sarandy M S. Classical correlation and quantum discord in critical systems[J]. Phys Rev A,2009,80(2):1-9. [16] Hase M, Terasaki I, Uchinokura K. Observation of the spin-Peierls transition in linear Cu2+(spin-1/2) chains in an inorganic compound CuGeO3[J]. Phys Rev Lett,1993,70(23):3651-3654. [17] Majumdar C K ,Ghosh D K. On next-nearest-neighbor interaction in linear chain. I[J]. J Math Phys,1969,10(8):1388-1398. [18] Majumdar C K. Antiferromagnetic model with known ground state[J]. J Phys C,1970,3(4):911-915. [19] Haldane F D M. Spontaneous dimerization in theS=1/2 Heisenberg antiferromagnetic chain with competing interactions[J]. Phys Rev B,1982,25(7):4925-4928. [20] Chen Shu, Wang Li, Gu Shijian,etal. Fidelity and quantum phase transition for the Heisenberg chain with next-nearest-neighbor interaction[J]. Phys Rev E,2007,76(6):1-4. [21] Wang Xiaoguang. Analytical results for entanglement in the five-qubit anisotropic Heisenberg model[J]. Physics Letters A,2004,329(6):439-444. QuqntumCorrelationintheHelsenbergSpinChainwithNext-nearest-neighbourInteraction HUANG Junlin, ZHANG Qingpao, HUANG Yaoyao, FAN Chuhui, SUN Zhe (College of Science, Hangzhou Normal University, Hangzhou 310036, China) This article studied the quantum correlation in the spin-1/2 antiferromagnetic Heisenberg spin chain with next-nearest-neighbor interaction by the concept of the quantum discord(QD). Due to theSU(2)symmetry andZ2symmetry, this article analytically calculated the GMQD in thisX-type state, found the relations between GMQD and the two sublattice correlation functions, and obtained the relationship between GMQD and energy eigenvalue. Based on the 4-sublattice and 6-sublattice cases, the results show that GMQD is determined by system parameters, and GMQD is an effective tool in detecting both the first-order and the infinite-order quantum-phase-transition points in the finite systems. quantum discord; geometric measure; quantum phase transition; Heisenberg spin chain 2013-04-03 2010年国家自然基金青年科学基金项目(11005027);杭州师范大学优秀中青年教师支持计划(HNUEYT 2011-01-011). 孙 哲(1981—),男,副教授,博士,主要从事量子信息理论、量子光学、凝聚态理论研究.E-mail: sunzhe_hznu@163.com 10.3969/j.issn.1674-232X.2013.04.016 O413.1MSC201081P40;65F15 A 1674-232X(2013)04-0365-08
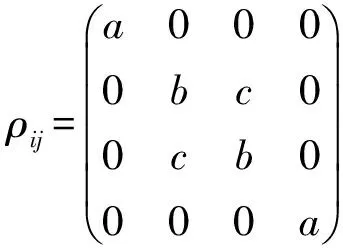
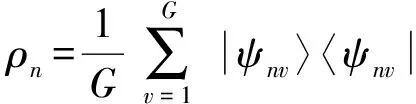


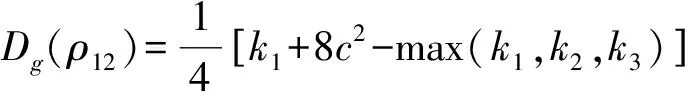



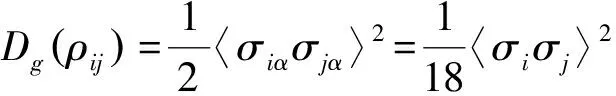




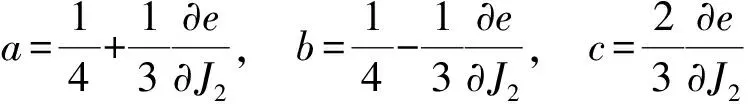

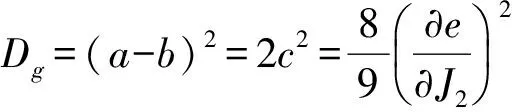
3 四格点以及六格点情况的解析计算
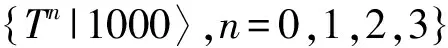
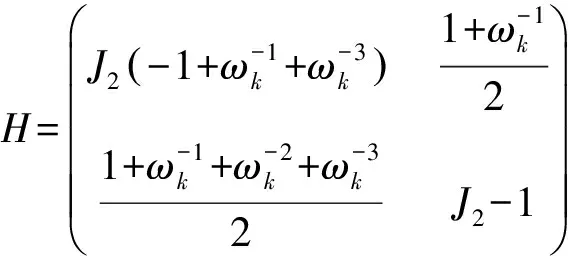

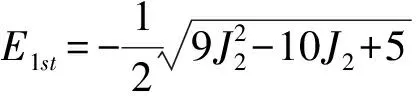




4 结 论
