马 彪

(杭州师范大学理学院,浙江 杭州 310036)

J-周期环及其扩张

马 彪

(杭州师范大学理学院,浙江 杭州 310036)

定义了J-周期环,推广了周期环.首先,讨论J-周期环的一些基本性质,如J-周期环的商环、子环以及J-周期环与周期环的关系.然后,给出J-周期环的一些扩张,并证明环的J-周期性与其上的幂级数环、广义矩阵环、上三角矩阵环的J-周期性是等价的.

周期环;J-周期环;Jacobson根;广义矩阵环;扩张

1 基本性质

设R是含单位元1的结合环,N(R),J(R),C(R)和U(R)分别表示环R中所有幂零元组成的集合,R的Jacobson根,R的中心和R中所有可逆元.环中元素x叫做potent元,如果存在整数n>1使得xn=x成立.环R叫做potent环,如果R中元素都是potent元.Jacobson[1]证明了所有的potent环都是交换环. 如果存在两个不相等的正整数m,n使得xm=xn成立，则环中元素x叫做周期元.如果R中元素都是周期元,则环R叫做周期环.显然,周期环是potent环的推广,但周期环可以是不交换的,例如M2(Z2).周期环的一个经典刻画由Chacron[2]给出,其指出一个环R是周期环当且仅当对R任意的元素x都存在一个正整数q和一个整系数多项式f(t)∈Z[t]使得xq=xq+1f(x).不难验证,x-xk∈N(R)能够得到xq=xq+1f(x),而x-xk∈N(R)又等价于xm-xn∈N(R).因此,环R是周期环当且仅当存在不同的正整数m,n使得xm-xn∈N(R).在上述条件中用J(R)代替N(R),我们得到新的一类环,它包含了所有的周期环.

定义1环R叫做J-周期环,如果对任意一个x∈R存在两个不同的正整数m,n使得

xm-xn∈J(R).

注该定义等价于说R是J-周期环当且仅当R/J(R)是周期环.

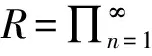
引理1J-周期环的同态像是J-周期环.

证明设π:R→S为环R到环S的满同态,其中R为J-周期环.如果x∈J(R),那么对任意的r∈R有1-xr∈U(R).于是对任意的s∈S,1-π(x)s∈U(S),所以有π(J(R))⊆J(S).对任意的s∈S存在r∈R使得π(r)=s.由R是J-周期环知存在不同的正整数m,n使得rm-rn∈J(R).因此,sm-sn=π(rm-rn)∈J(S),即S是一个J-周期环.

引理2环R是J-周期环当且仅当对R中任意的x都存在正整数n,k使得(x-xn)k∈J(R).

推论1一个环R是周期环当且仅当R是J-周期环且J(R)是诣零的.

证明设R是一个J-周期环并且J(R)是诣零的,那么对任意的x∈R存在不同的正整数m,n使得xm-xn∈J(R)⊆N(R),所以R是周期环.反过来,如果R是周期环,则J(R)是诣零的[3].

推论2设R是一个J-周期环并且R是除环,则R是一个域.

证明R是除环则J(R)=0.因此,R是一个周期的除环.由文献[3]，R是一个域.

环R的一个理想I叫做约化理想,如果由a2∈I能够得到a∈I.显然,I是一个约化理想当且仅当R/I是一个约化环.

推论3设R是一个J-周期环,如果J(R)是一个约化理想则R/J(R)是交换环.

证明如果J(R)是一个约化理想,那么R/J(R)是约化环.由引理2,R/J(R)是一个potent环,因此是交换环.

推论4设R是一个J-周期环,如果J(R)是一个约化理想并且J(R)⊆C(R),则R是交换环.

证明如果R满足上述条件,由引理2，对任意的x∈R存在正整数k使得x-xk∈J(R)⊆C(R).由文献[4],R是交换环.

设R是一个周期环,S是R的一个子环,则对任意的s∈S,存在不同的正整数m,n使得sm-sn∈J(R).因此,对任意的r∈R有1-(sm-sn)r∈U(R).特别的,对任意的s′∈S有1-(sm-sn)s′∈U(R),但1-(sm-sn)s′未必是S中的可逆元.所以J-周期环的一个子环未必是J-周期环.当然,如果1-(sm-sn)s′∈U(S),那么S一定是J-周期环.自然地,我们得到下面的定理.

定理1设R是一个J-周期环,S是R的一个子环.对s∈S,如果s∈U(R)就有s∈U(S),那么S是一个J-周期环.

设e是环R中的一个幂等元,集合eRe关于R中的加法和乘法构成一个环,叫做R的corner环,其单位元为e.下面的定理给出了J-周期环与其corner环的关系.

定理2环R是J-周期环当且仅当对R中任意的幂等元e,eRe是J-周期环.

证明如果R是J-周期环,那么对任意的eae∈eRe⊆R,存在不同的正整数m,n使得(eae)m-(eae)n∈J(R).因为J(eRe)=eJ(R)e,且(eae)m-(eae)n∈eJ(R)e=J(eRe),所以eRe是J-周期环.反过来,如果对任意的幂等元e有eRe是J-周期环,那么取e=1立即得到R是J-周期环.

2 扩 张

定理3环R是J-周期环当且仅当幂级数环R[[x]]是J-周期环.

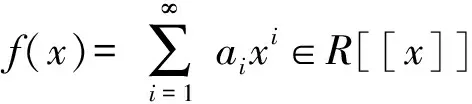
引理3设R是任意一个环,则R[[x]]/(xn)≅Sn(R),其中

证明定义映射φ:R[[x]]→Sn(R)为

其中f(x)=a0+a1x+…+an-1xn-1+….不难验证φ是环R[[x]]到环Sn(R)的一个满同态.因为

由环同构定理,R[[x]]/(xn)≅Sn(R).

推论5对于环R,下面的说法等价:

1)R是J-周期环.

2)R[[x]]是J-周期环.

3)Sn(R)是J-周期环.

证明1)⟹2)，由定理3可得.2)⟹3)，由定理3、引理3及引理1可得.3)⟹1)，对任意的r∈R,令

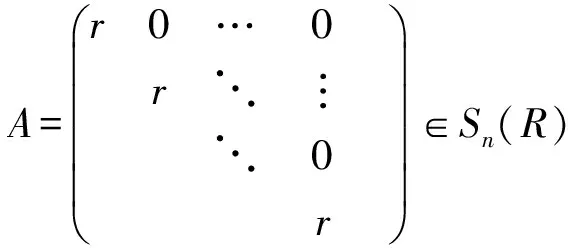
那么存在不同的正整数m,n使得Am-An∈J(Sn(R)).因为

所以rm-rn∈J(R),因此R是一个J-周期环.

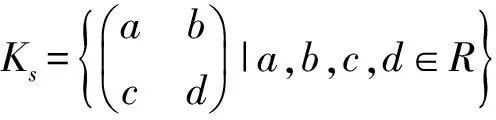
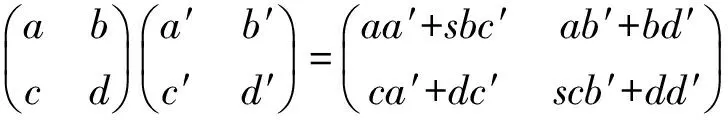
构成一个环,叫做R上关于乘子s的广义矩阵环.

引理4[6]设R是一个环,Ks是R上关于乘子s的广义矩阵环.则

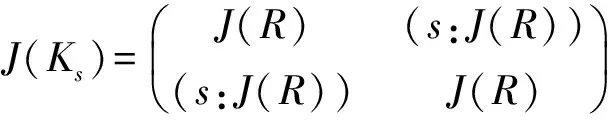
其中(s:J(R))={r∈R|rs∈J(R)}.特别地,如果s∈C(R)∩J(R),那么

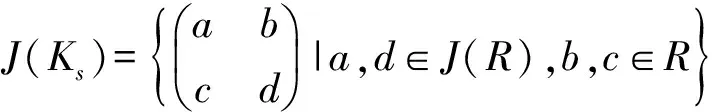
下面关于周期元的引理可以在文献[7]中找到证明.为了方便读者阅读,我们给出一个比较简单的证明.

引理5对任意的两个周期元a,b,存在不同的正整数k,l使得ak=al且bk=bl.

证明设a,b为周期元,那么存在正整数n,s≥1使得an+s=an以及正整数m,t≥1使得bm+t=bm.两个式子两边分别乘am和bn得到an+m+s=an+m且bm+n+t=bm+n.令k=m+n+st,l=m+n,则

ak=am+n+st=am+n+sas(t-1)=am+n+s(t-1)=…=am+n=al

且

bk=bm+n+st=bm+n+tb(s-1)t=bm+n+(s-1)t=…=bm+n=bl.

因为s,t≥1,所以k,l是不相等的正整数,这样就证明了引理.

显然,引理5的结论可以推广到任意有限个周期元的情形.

定理4设R是一个环,s∈C(R)∩J(R),则R是J-周期环当且仅当Ks也是J-周期环.

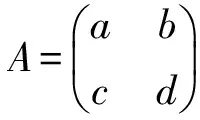
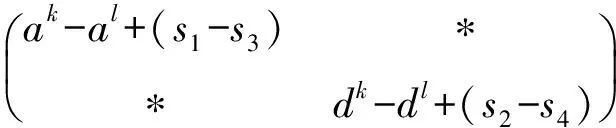
其中s1,s2,s3,s4∈J(R).因为ak-al∈J(R)且dk-dl∈J(R)，利用引理4可得Ak-Al∈J(Ks),因此Ks是J-周期环.

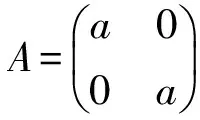
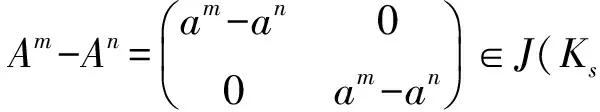
由引理4,am-an∈J(R),因此R是J-周期环.

对任意的环R,设n>1为一固定的正整数,记Tn(R)为R上所有n阶上三角矩阵组成的集合.Tn(R)关于通常的矩阵加法和乘法构成一个环,称为R上的n阶上三角矩阵环.利用引理5,还可以证明J-周期环的上三角矩阵环也是J-周期环.

定理5环R是J-周期环当且仅当Tn(R)也是J-周期环.

证明设R是J-周期环.对任意固定的正整数n>1,Tn(R)为R上的n阶上三角矩阵环.对任意的

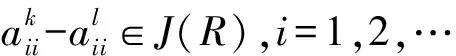
因为

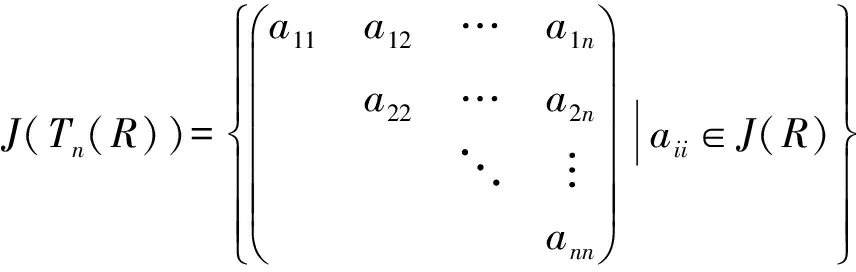
所以Ak-Al∈J(Tn(R)).这表明Tn(R)是J-周期环.

反过来,设Tn(R)是周期环.对任意的x∈R,令X=diag{r,r,…,r}∈Tn(R).因为Tn(R)是J-周期环,所以存在不同的正整数m,n使得Xm-Xn∈J(Tn(R)),从而rm-rn∈J(R).因此R是周期环.

推论6环R是J-周期环当且仅当R的平凡扩张也是J-周期环.

由引理5立即可以得到,任意有限个J-周期环的直和也是J-周期环.下面证明有限个J-周期环的直和的一类子环也是J-周期环.

定理6设R1,R2是J-周期环,则R1,R2的亚直和R也是J-周期环.

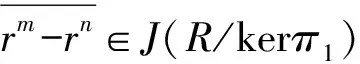
下面考虑J-周期环的另一类扩张,这类扩张和子环有关.

定义3[8].设D是一个环,C是D的一个子环,记

R[D,C]={(d1,d2,…,dn,c,c,…)|di∈D,c∈C,n≥1},

则R[D,C]关于对应分量的加法和乘法构成一个环.

引理6[8]设D是一个环,C是D的一个子环,则J(R[D,C])=R[J(D),J(C)∩J(D)].

定理7设D是一个环,C是D的一个子环,则R[D,C]是J-周期环当且仅当C,D都是J-周期环并且对每个a∈J(C)存在正整数n使得an∈J(D).

证明设R[D,C]是一个J-周期环.对任意的d∈D和c∈C,分别令x=(d,0,…)∈R[D,C]和y=(c,c,…)∈R[D,C].那么存在两对不同的正整数m,n和s,t分别使得xm-xn∈J(R[D,C])和ys-yt∈J(R[D,C]).由引理6有dm-dn∈J(D)及cs-ct∈J(D)∩J(C).因此,D和C都是J-周期环.如果a∈J(C),令z=(a,a,…),那么存在不同的正整数k,l使得zk-zl∈J(R[D,C]).所以ak-al∈J(D).不妨设l>k,则ak(1-al-k)∈J(D).因为a∈J(C),所以1-al-k∈U(R),因此有ak∈J(D).

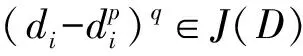
[1] Jacobson N. Structure of rings,AMS Colloq Publ Vol 37[M]. Providence R I: American Mathematical Society,1964:217.

[2] Chacron M. On a theorem of Herstein[J]. Canad J Math,1969,21:1348-1353.

[3] Grosen J, Tominaga H, Yaqub A. On weakly periodic rings, periodic rings and commutativity theorems[J]. Math J Okayama Univ,1990,32:77-81.

[4] Herstein I N. A generalization of a theorem of Jacobson III[J]. Amer J Math,1953,75:105-111.

[5] Krylov P A. Isomorphism of generalized matrix rings[J]. Algebra Logic,2008,47(4):258-262.

[6] Krylov P A, Tuganbaev A A. Modules over formal matrix rings[J]. J Math Sci,2010,171(2):248-295.

[7] Itani H W. Structure of rings with conditions involving periodic, potent, and central elements[D]. Beirut: American University of Beirut,2009.

[8] 程恭品.环R[D,C]的结构及其刻画[D].南京:东南大学,2006.

J-periodicRingandExtensions

MA Biao

(College of Science, Hangzhou Normal University, Hangzhou 310036, China)

This paper definedJ-periodic ring which generalized the concept of periodic ring. Firstly, some elementary properties ofJ-periodic rings were studied, such as the quotient rings and subrings ofJ-periodic rings as well as the relationship betweenJ-periodic rings and periodic rings. Then some extensions ofJ-periodic rings were provided, and the equivalence of theJ-periodicity of a ring and theJ-periodicity of the power series ring, generalized matrix ring and upper triangular matrix ring over it was proved.

periodic ring;J-periodic ring; Jacobson radical; generalized matrix ring; extension

2013-03-20

杭州师范大学创新种子基金项目.

马彪(1989—),男,基础数学专业硕士研究生,主要从事代数研究.E-mail: 1989mabiao@sina.com

10.3969/j.issn.1674-232X.2013.04.014

O153.3MSC201013M05

A

1674-232X(2013)04-0354-05