吴倩 聂建栋 卫红凯

(1．海军工程大学振动与噪声研究所，船舶振动噪声重点实验室，武汉 430033)(2．海军驻武汉四三八厂军事代表室，武汉 430033)(3．海军工程大学电子工程学院，武汉 430033)

分数阶Fourier变换域极值搜索的混沌优化算法研究

吴倩1†聂建栋2卫红凯3

(1．海军工程大学振动与噪声研究所，船舶振动噪声重点实验室，武汉 430033)(2．海军驻武汉四三八厂军事代表室，武汉 430033)(3．海军工程大学电子工程学院，武汉 430033)

正如傅里叶变换采用正弦基，单频信号能够在频域形成峰值，分数阶Fourier变换采用线性调频基，线性调频(LFM)信号能够在分数阶Fourier域上实现聚焦，利用此聚焦性通过搜索峰值可实现LFM信号检测和参数估计．通常采用步进式搜索方法，效率低下．为了克服该缺点，通过对分数阶Fourier域优化问题本质的研究，将混沌优化算法引入到分数阶Fourier域极值搜索中．仿真结果表明:本文的方法优于传统的步进式搜索法．

混沌优化算法， 分数阶Fourier变换， 极值搜索

引言

传统的傅立叶变换(FFT)采用正弦基，适合于处理平稳信号．但实际中，许多信号的统计特性往往随时间变化，表现出非平稳特性．为了表征非平稳信号的时变特征，需要寻求新的时频分析工具，分数阶 Fourier变换(FRFT)［1］－［3］是近年来基于此出现的一种新的信号处理方法．FRFT采用线性调频基，特别适合于处理 Chirp类信号．线性调频(LFM)信号在特定的分数阶Fourier域上能够实现聚焦，称为LFM信号在分数阶Fourier域具有聚焦性．常用此聚焦特性检测在通信、雷达、声纳等领域中应用广泛的LFM信号．

目前，常用的LFM信号检测方法是步进法［4］－［6］．即设定参数步长，在分数阶 Fourier 域二维平面对LFM信号进行步进搜索．但步进式搜索算法效率低下，尤其是当精度要求高时，更是如此．通常离散采样信号经FRFT后，除了对应LFM信号的最大峰值外，在分数阶Fourier域平面还会出现多个局部峰值．因此，分数阶Fourier域的极值搜索本质上是全局寻优问题．混沌优化算法［7］－［10］是近年来出现的一种全局优化算法，该法利用混沌的遍历性进行搜索，具有所需函数信息少、不依赖于初始值等优点．因此，本文将混沌优化算法引入到FRFT中，提出了一种基于混沌优化算法的分数阶Fourier域极值优化算法，从而实现LFM信号的检测．通过仿真实例，验证了本文所提方法的效率优于传统的步进式搜索方法．

1 分数阶Fourier域优化问题描述

分数阶 Fourier变换由 Namias于1980年提出［1］，可理解为信号在时频平面的旋转算子．其定义如下:

其中，Kp(u，t)为核函数，如式(2)所示:

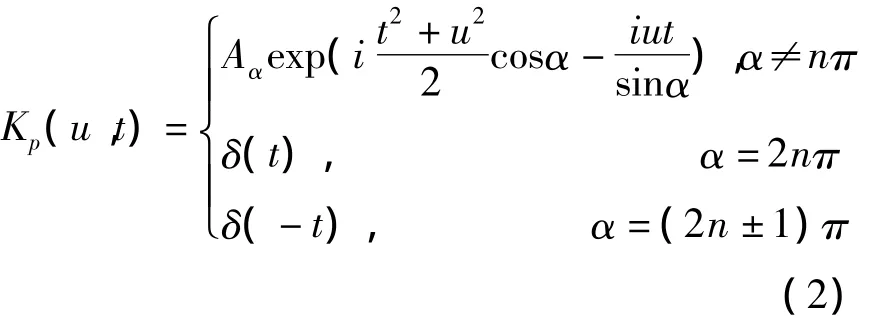
信号在分数阶Fourier域上的旋转角度为:α=pπ/2，Aα为相应的幅度因子，其表达式为:Aα=

实际中，信号由离散化采样值表示．因此，需要将连续分数阶Fourier变换离散化，本文采用Ozaktas［3］提出的离散化快速算法，即:则分数阶Fourier域二维极值搜索问题可描述为:

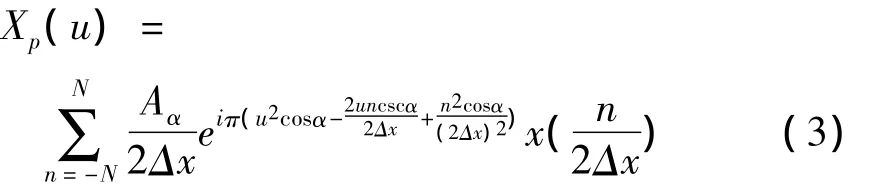
在分数阶Fourier域二维平面(p，u)内，寻找合适的(p0，u0)，使得分数阶Fourier域目标函数f(p，u)=|Xp(u)|2达到最大，其数学表达式为:

由式(3)和(4)可知，分数阶Fourier域目标函数形式复杂，为多个二维复杂指数函数的非线性叠加．这使得信号经FRFT后，目标函数呈现出非凸、多峰等特性．进一步增加了分数阶Fourier域二维寻优的难度．

2 混沌优化算法

混沌是存在于非线性动力学系统中的一种普遍的行为．混沌的变化过程看似杂乱无章，实则有其内在的规律性．混沌变量具有随机性、遍历性、规律性等特点．利用混沌变量的遍历性作为函数极值搜索过程中避免陷入局部极小值的优化机制，李兵［9］等提出了一种新的全局优化算法－混沌优化算法．

混沌优化算法的基本思想是根据一定的混沌映射，产生混沌序列，通过载波方式将混沌序列载入到参变量区间，并比较各序列的目标函数值．通常以一定步数内，函数值不发生变化作为终止条件，以满足终止条件时的当前值作为最优值输出．其基本步骤为:

(1)根据具体待优化问题，得到解空间，并根据一定的混沌映射，产生各解空间的混沌序列，各混沌序列数为M，同时令计数变量m=1．

(2)一次载波．设解空间维数为D，以y=［y1，…，yD］表示解空间向量，各变量yd|d=1，…，D范围为ad到bd．将各解空间的混沌序列通过下式所示的载波方式载入到各解空间变量所对应的范围内．

其中，xdm对应第d(d=1，…，D)维解空间的第m(m=1，…，M)个混沌变量．

(3)选择合适的度量函数f，并计算ym(第m个混沌变量对应的解向量)的度量函数值f(ym)．当初始状态即m=1时，以其对应的y1及f(y1)作为初始最好解fb及最佳变量yb．否则，将ym与fb比较，找出其中的最佳值，与此对应，将最佳变量yb做相应变化．

(4)判断是否达到设定搜索步数，若是，则往下运行步骤(5)．否则，计数变量m增加1，运行步骤(2)－(4)．

(5)缩小搜索空间，并对混沌变量进行二次载波，继续搜索，，将当前搜索值与以前搜索的历史最好解比较，若当前值由于历史最好解，则将当前值作为最好解，同时更新最佳变量．

(6)判断是否满足终止条件，若满足，则停止运算，并以当前解作为最优解输出，否则，重复步骤(5)，继续进行搜索．

对于分数阶Fourier域极值寻优问题，以式(4)中的最小化目标函数作为混沌优化算法中度量函数．典型的混沌映射序列有式(6)所示的Logistic映射、式(7)所示无限折叠映射等．由于无限折叠映射的遍历性更均匀，因此，本文中采用无限折叠映射．

算法流程如图1所示．

图1 混沌优化算法流程图Fig．1 The schedule of chaos optimization algorithm

3 仿真实例

下面通过几个实例来说明混沌优化算法的良好性能．

1、信号x(t)=ei2πf0t+iπμt2+w(t)，t∈［0，T］．信号脉宽T=0．1s，采样频率fs=2500Hz，带宽为 150 －300Hz．w(t)是高斯白噪声，信噪比 －5dB．步进法(直接法)和混沌优化算法的优化结果如表1所示．

表1 0．1s脉宽时直接法与混沌优化算法性能比较Table 1 Comparison of the results for step－based method and chaos optimization algorithm with 0．1s pulse width

2、信号x(t)=ei2πf0t+iπμt2+w(t)，t∈［0，T］．信号脉宽T=0．2s，采样频率fs=2500Hz，带宽为 150 －350Hz．w(t)是高斯白噪声，信噪比 －5dB．步进法(直接法)和混沌优化算法的优化结果如表2所示．

表2 0．2s脉宽时直接法与混沌优化算法性能比较Table 2 Comparison of the results for step－based method and chaos optimization algorithm with 0．2s pulse width

3、信号x(t)=+w(t)，t∈［0，T］．信号脉宽T=0．4s，采样频率fs=2500Hz，带宽为 150 －370Hz．w(t)是高斯白噪声，信噪比 －5dB．步进法(直接法)和混沌优化算法的优化结果如表3所示．

表3 0．4s脉宽时直接法与混沌优化算法性能比较Table 3 Comparison of the results for step－based method and chaos optimization algorithm with 0．4s pulse width

4、信号x(t)=+w(t)，t∈［0，T］．信号脉宽T=0．6s，采样频率fs=2500Hz，带宽为150－360Hz．w(t)是高斯白噪声，信噪比 －5dB．步进法(直接法)和混沌优化算法的优化结果如表4所示．

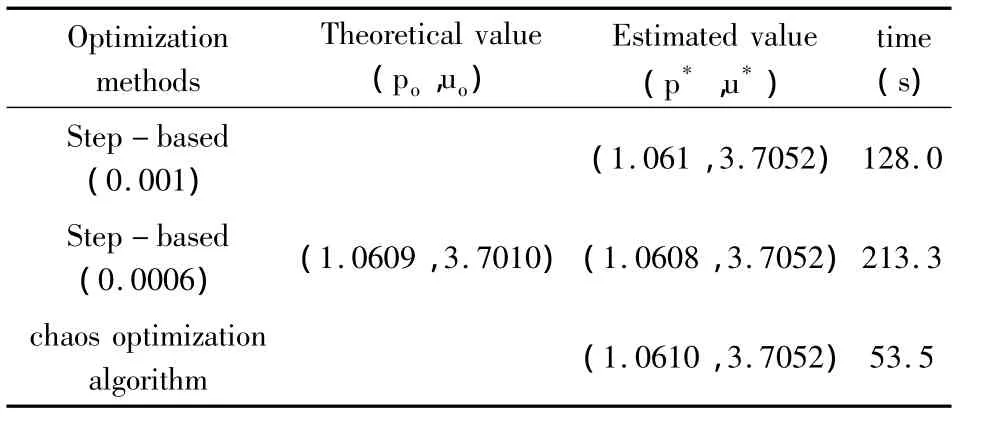
表4 0．6s脉宽时直接法与混沌优化算法性能比较Table 4 Comparison of the results for step－based method and chaos optimization algorithm with 0．6s pulse width

表1－4中，估计值和理论值有偏差，这是由于信号的离散化采样及噪声的影响导致的．直接法的计算时间和估计精度与步长有关，随着步长的增加，尽管其估计精度提高，但以牺牲运算效率为代价．混沌优化算法不仅耗时少于直接法，且其精度高．

4 结束语

本文通过研究分数阶Fourier域极值优化问题的本质，将混沌优化算法引入到分数阶Fourier域极值搜索中，和传统步进式搜索算法相比，提高了搜索速度和精度．

研究表明:

(1)线性调频信号在分数阶Fourier域具有聚焦性，其目标函数表现出非凸、多峰等特性，增加了极值搜索的难度．

(2)混沌优化算法利用混沌的遍历性进行全局搜索，分数阶Fourier域极值搜索中采用混沌算法，其搜索效率和精度优于传统步进式搜索算法

(3)文中思想对于混沌在优化领域的应用，提供了典型案例，具有推广价值．

1 Namias V．The fractional order Fourier transform and its application to quantum mechanics．Journal of the Institute of Mathematics and its Applications，1980，25(3)，241 ～265

2 Ozaktas H M，Mendlovic D．Fractional Fourier transforms and their optical implementation．Journal of the Optical Society America A，1993，10(12)，2522～2531

3 Ozaktas H M，Arikan O，Kutay A．Digital computation of the fractional fourier transform．IEEE Transactions on Signal Processing，1996，44，2141～2150

4 张淑宁，赵惠昌，吴冰．基于分数阶傅立叶变换的伪码体制引信线性调频干扰抑制技术．兵工学报，2006，27(1):32～36(Zhang S N，Zhao H C，Wu B．LFM interference excision technique in pseudo～random code fuse based on fractional Fourier transform．Acta Armamentarll，2006，27(1):32～36(in Chinese))

5 赵兆，是湘全．一种基于分数阶Fourier变换的雷达运动目标检测算法．电讯技术，2007，47(4):95～98(Zhao Z，Shi X Q．A moving targets detection algorithm based on fractional Fourier transform．Telecommunicaiton Engineering，2007，47(4):95～98(in Chinese))

6 董永强，陶然，周思永，王越．含未知参数的多分量Chirp信号的分数阶傅里叶分析．北京理工大学学报，1999，19(5):612～616(Dong Y Q，Tao R，Zhou S Y，Wang Y．The fractional Fourier analysis of multicomponent chirp signals with unknown parameters．Journal of Beijing Insti-tute of Technology，1999，19(5):612 ～ 616(in Chinese))

7 Liu S S，Hou Z J．Weighted gradient direction based chaos optimization algorithm for nonlinear programming problem．In:Proceedings of 4th World Congress on Intelligent，Control and Automation，2002，1779～1783

8 高雷阜，胡行华．不同混沌序列对全局最优解的搜索影响．辽宁工程技术大学学报(自然科学版)，2008，27(4):629～631(Gao L F，Hu X H．Effect of different chaotic sequences on seeking overall optimal solution．Journal of Liaoning Technical University(Natural Science)，2008，27(4):629～631(in Chinese))

9 李兵，蒋慰孙．混沌优化方法及其应用．控制理论与应用，1997，14(4):613～615(Li B，Jiang W S．Chaos optimization method and its application．Control Theory and Application，1997，14(4):613～615(in Chinese))

10 单梁，强浩，李军，王执铨．基于Tent映射的混沌优化算法．控制与决策，2005，20(2):179～182(Shan L，Qiang H，Li J，Wang Z Q．Chaotic optimization algorithm based on tent map．Control and Decision，2005，20(2):179～182(in Chinese))

† Corresponding author E－mail:wuqian0930@qq．com

STUDY OF CHAOS OPTIMIZATION ALGORITHM IN THE FOURIER DOMAIN FOR EXTREMUM SEARCHING

Wu Qian1†Nie Jiandong2Wei Hongkai3
(1．Institute of Noise＆Vibration，National Key Laboratory on Ship Vibration＆Noise，Navy Engineering University，Wuhan430033，China)(2．Navy military delegate section office of438factory，Wuhan430033，China)(3．Electronic Engineering College，Navy Engineering University，Wuhan430033，China)

As the sinusoidal signal can be concentrated in the Fourier domain due to the orthonormal sine basis of the Fourier transform．The linear frequency modulation(LFM)signal can be concentrated in the fractional Fourier domain due to its orthonormal chirped basis of the fractional Fourier transform．So the detection and parameter estimation of LFM signal is usually completed by step－based searching method for extremum searching in the fractional Fourier domain．In order to resolve the disadvantage of inefficiency of step－based searching method，Chaos optimization algorithm is introduced to the fractional Fourier transform for extremum searching based on the study for the nature of fractional Fourier optimization problem．Simulation results show that the performance of Chaos optimization algorithm is better than that of the traditional step－based method．

chaos optimization algorithm， fractional Fourier transform， extremum searching

24 April 2013，

5 June 2013．

10．6052/1672－6553－2013－056

2013－04－24 收到第 1 稿，2013－06－05 收到修改稿．

E－mail:wuqian0930@qq．com