宋端 刘世兴

(1．辽东学院影像物理教研室，丹东 118001)(2．辽宁大学物理学院，沈阳 110036)

Birkhoff意义下Hojman－Urrutia方程的离散变分计算*

宋端1刘世兴2†

(1．辽东学院影像物理教研室，丹东 118001)(2．辽宁大学物理学院，沈阳 110036)

在Birkhoff框架下，采用离散变分方法研究了非Hamilton系统－Hojman－Urrutia方程的数值解法，并通过和传统的Runge－Kutta方法进行比较，说明了在Birkhoff框架下研究这类不具有简单辛结构的非Hamilton系统可以得到更可靠和精确的数值结果．

Birkhoff方程， Hojman－Urrutia方程， 非Hamilton系统， 离散变分计算

引言

Hamilton系统具有简单的辛结构，自动满足自伴随性质，可以用来描述耗散可忽略的保守动力学系统，并在动力学系统的保结构算法研究中具有重要意义［1，2，3］．但是对于本质非自伴随的动力学系统，在保持实验室可观测量或动力学函数物理意义不变的情况下，则不能表示为Hamilton系统．虽然通过Darboux变换，可以实现简单的辛结构表示，但是此时的实验室可观测量或动力学函数已经失去了直接的物理意义，我们称这类不能表示为简单Hamilton方程的动力学系统为非Hamilton系统［4］．对于非Hamilton系统，由于不具有简单的辛结构，Hamilton系统的保辛算法已经不再适用，因此需要找到一种较理想的数值算法来数值求解这类非Hamilton系统的运动方程问题．

本文以 Hojman－Urrutia(H－U)方程［5－7］为例，在Birkhoff意义下，将H－U方程表示为自治Birkhoff方程的形式，并采用离散变分方法，给出研究这类非Hamilton系统的数值积分子．通过数值实验说明了在Birkhoff框架下研究非Hamilton系统的几何数值积分问题是合理和有效的，从而为非Hamilton系统的几何数值积分问题研究开辟了一条新的途径．

1 Hojman－Urrutia 方程的 Birkhoff表示

Hojman和Urrutia于1981年在J．Math．Phys．上发表了一篇文章，在该文中，他们给出了如下的方程［6，7］:

称为Hojman－Urrutia方程．该方程在关于Lagrange逆问题和Hamilton逆问题的研究以及Birkhoff力学的发展过程中起着重要的作用［7］．

取如下初始条件:

则方程(1)有如下的解析解:

方程(1)看似简单，却不能表示成Lagrange方程或Hamilton正则方程的形式，因此其是一个典型的非Hamilton系统问题，其一阶形式没有辛结构．但是在Birkhoff力学框架下，该方程可以表示为满足自伴随条件的Birkhoff方程的形式，具有简单的辛结构．如果取a1=x，a2=y，a3=x，a4=y，利用Hojman方法可以构造该系统的 Birkhoff表示［5，6］

对应的Birkhoff方程为:

从所得到的Birkhoff函数和 Birkhoff函数组(4)可以看出，H－U方程的Birkhoff表示方程(5)是自治Birkhoff方程．

2 离散自治Birkhoff方程和变分积分子

给定构型空间为M2n，其坐标为{aμ}(μ=1，…，2n)，设自治Birkhoff函数B:M2n→R和Birkhoff函数组Rμ:M2n→R，从而定义如下Pfaff作用量:

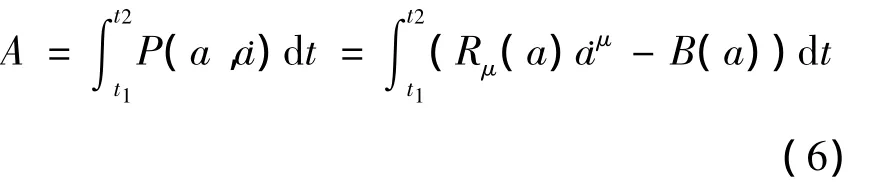
这里P(a，a)为Pfaff函数．利用等时变分原理δA=0，并考虑端点条件 δa(t1)= δa(t2)=0，可以得到如下自治 Birkhoff方程［6，8］:

则由方程(7)所描述的系统被称为自治Birkhoff系统［8］．

取离散空间为M×M，并取定时间步长h∈R，定义离散Pfaff函数Pd:M×M×R→R，从而给出离散作用泛函为［9，10］:

利用离散变分计算δAd=0，并考虑端点条件δa0=δaN=0，则可以得到如下离散自治Birkhoff方程:

这里，DB为离散Birkhoff映射，写成坐标形式如下:

这里DiPd(i=1，2)表示对Pd中第i个变量的偏导数．如果取

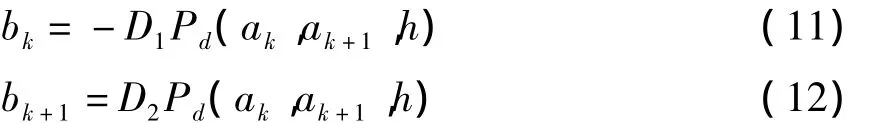
作为中间变量，通过求解隐式方程(11)可以得到ak+1，然后求解显式方程(12)，则得到映射(ak，bk)→(ak+1，bk+1)，即给出系统随时间的演化．可以证明，映射保持离散 Birkhoff辛形式［9］，从而方程(11)和(12)给出了计算自治Birkhoff系统的Birkhoff辛积分子．可以采用许多方法离散Pfaff函数，如中点格式，Verlet方法，Runge－Kutta方法等［11］．本文采用Euler中点格式来离散Pfaff函数．

3 Hojman－Urrutia方程的离散变分计算

由H－U方程的 Birkhoff表示(4)式可以得到H－U方程所对应的Pfaff函数:

从而利用Euler中点格式可以得到离散Pfaff函数:

利用(11)和(12)式可以得到如下表达式

从方程组(15)可以求解出(i=1，…，4)，将其代入方程组(16)，则得到(i=1，…，4)，这样就得到了Hojman－Urrutia方程的数值解，从而得出系统随时间的演化．

这里取时间步长h=0．0001，在上面的初始条件(2)下，对 H－U 方程(1)采用2 阶 Runge－Kutta方法，对H－U方程对应的等价Birkhoff方程(4)采用本文所给的离散变分方法分别进行数值计算，并比较两种框架下所得结果的误差，如图1和图2所示．

图1 x的相对误差Fig．1 The relative error of x

图2 y的相对误差Fig．2 The relative error of y

图1和图2分别表示计算所得的x和y的相对误差，实线表示在Birkhoff框架下采用离散变分方法算得的结果，而点线表示在原方程框架下采用2阶R－K方法算得的结果，从图中可以看出，在Birkhoff框架下，采用离散变分方法算得的数值误差更小，结果要优于在原方程框架下算得的结果．

4 结论

通过对Hojman－Urrutia方程的数值研究，说明在求解这类不能表示成Hamilton方程或Lagrange方程的非Hamilton系统的数值解时，为了得到更好的数值结果，可以将该系统的运动方程转化为具有自伴随特性的Birkhoff方程的形式，从而在Birkhoff框架下研究非Hamilton系统的数值积分问题，以得到更加可靠、精确的数值结果．

1 冯康，秦孟兆．哈密尔顿系统的辛几何算法．杭州:浙江科学技术出版社，2003(Feng K，Qin M Z．Symplectic geometric algorithms for hamiltonian systems．Hangzhou:Zhejiang Science and Technology Press，2003(in Chinese))

2 Hairer E，Lubich C，Wanner G．Geometric numerical integration structure－preserving algorithms for ordinary differential equations．Springer，2002

3 高强，钟万勰．Hamilton系统的保辛守恒积分算法．动力学与控制学报，2009，7(3):193～199(Gao Q，Zhong W X．The symplectic and energy preserving method for the integration of hamilton system．Jouranal of Dynamics and Control，2009，7(3):193 ～ 199)

4 刘畅，宋端，刘世兴，郭永新．非齐次Hamilton系统的Birkhoff表示．中国科学:物理学、力学、天文学，2013，43(3):541～548(Liu C，Song D，Liu S X，Guo Y X．Birkhoffian representation of non－homogenous Hamiltonian systems．Scientia Sinica Physica，Mechanica and Astronomica，2013，43(3):541～548(in Chinese))

5 梅凤翔，刘瑞，罗勇．高等分析力学．北京:北京理工大学出版社，1991(Mei F X，Liu D，Luo Y．Advanced analytical mechanics．Beijing:Beijing Institute of Technology Press，1991(in Chinese))

6 梅凤翔，史荣昌，张永发，吴惠彬．Birkhoff系统动力学．北京:北京理工大学出版，1996(Mei F X，Shi R C，Zhang Y F and Wu H B．Dynamics of birkhoff systems．Beijing:Beijing Institute of Technology Press，1996(in Chinese))

7 梅凤翔．关于Whittaker方程和Hojman－Urrutia方程．力学与实践．2012，34:62～63(Mei F X．About whittaker equation and Hojman－Urrutia equation．Mechanics in Engineering，2012，34:62～63(in Chinese))

8 Santilli R M ．Foundations of theoretical mechanicsⅡ:Birkhoffian generalization of Hamiltonian mechanics．New York:Spring－verlag，1983

9 Liu S X，Liu C，Guo Y X．Geometric formulations and variational integrators of discrete autonomous Birkhoff systems．Chinese Physics B，2011，20(3):034501

10 刘世兴，刘畅，郭永新．Birkhoff意义下Henon－Heiles方程的离散变分计算．物理学报，2011(6):060000(Liu S X，Liu C，Guo Y X．Discrete variational calculation of Henon－Heiles equation in the Birkhoffian sense．Acta Physica Sinica，2011，60(6):060000(in Chinese))

11 Marsden J E，West M．Discrete mechanics and variational integrators．Acta Numerica，2001，357～514

*The Project supported by the National Natural Science Foundation of China(11202090，11172120，10932002)

† Corresponding author E－mail:liushixing@lnu．edu．cn

DISCRETE VARIATIONAL CALCULATION OF HOJMAN-URRUTIA EQUATION IN THE BIRKHOFFIAN SENSE*

Song Duan1Liu Shixing2†Guo Yongxin1，2
(1．Eastern Liaoning University，Physics of medical imaging department，dandong118001，China)(2．College of Physics，Liaoning University，Shenyang110036，China)

By using the discrete variatonal method in the framework of Birkhoffian systems，this paper researched the numerical algorithms of Hojman－Urrutia equation，which is a non－Hamiltonian system．Compared with Runge－Kutta method，the numerical results show that the more reliable and accurate numerical results can be obtained when the non－Hamilton systems that have not simple symplectic structure are studied in the Birkhoffian sense．

Birkhoff’s equations， Hojman－Urrutia equation， non － Hamilton system， discrete variational methods

17 September 2012，

16 April 2013．

10．6052/1672－6553－2013－060

2012－09－17 收到第 1 稿，2013－04－16 收到修改稿．

*国家自然科学基金资助项目(11202090，11172120，10932002)

E－mail:liushixing@lnu．edu．cn