LIU Xi-min (刘喜敏)

Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China

Traffic and Transportation Engineering College and Key Laboratory of Road Structure and Material of Communication Ministry, Changsha University of Science and Technology, Changsha 410114, China,

E-mail: roadtrafficuliu@126.com

LU Shou-feng (卢守峰)

Traffic and Transportation Engineering College, Changsha University of Science and Technology, Changsha 410114, China

(Received October 31, 2012, Revised February 18, 2013)

Applying the maximum information principle to cell transmission model of traffic flow*

LIU Xi-min (刘喜敏)

Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China

Traffic and Transportation Engineering College and Key Laboratory of Road Structure and Material of Communication Ministry, Changsha University of Science and Technology, Changsha 410114, China,

E-mail: roadtrafficuliu@126.com

LU Shou-feng (卢守峰)

Traffic and Transportation Engineering College, Changsha University of Science and Technology, Changsha 410114, China

(Received October 31, 2012, Revised February 18, 2013)

This paper integrates the maximum information principle with the Cell Transmission Model (CTM) to formulate the velocity distribution evolution of vehicle traffic flow. The proposed discrete traffic kinetic model uses the cell transmission model to calculate the macroscopic variables of the vehicle transmission, and the maximum information principle to examine the velocity distribution in each cell. The velocity distribution based on maximum information principle is solved by the Lagrange multiplier method. The advantage of the proposed model is that it can simultaneously calculate the hydrodynamic variables and velocity distribution at the cell level. An example shows how the proposed model works. The proposed model is a hybrid traffic simulation model, which can be used to understand the self-organization phenomena in traffic flows and predict the traffic evolution.

kinetic traffic model, Cell Transmission Model (CTM), maximum information principle, traffic flow, velocity distribution

Introduction

The models for vehicular traffic flows can be divided into macroscopic, mesoscopic and microscopic ones. For the macroscopic model, the related variables are directly the velocity, density and flow flux. For the mesoscopic model, the main concern is the velocity distribution. For the microscopic model, the first concern is the microscopic driving behavior. In the present paper, we focus ourselves on the mesoscopic model.

Until now, the approaches to the evolution equations of velocity distribution can be summarized as three ones. The first approach is the Boltzmann-like treatments, which was initiated from a pioneered mesoscopic model. The second one is to use encounter rate and table of games, which is called the methods of discrete mathematical kinetic theory. The third one is to construct the lattice Boltzmann model of velocity distribution. The details can be referred to Ref.[1].

Vehicular traffic can be modeled as a system of interacting particles driven far from equilibrium. Using statistical physics methods to study vehicular traffic offers the possibility to examine various fundamental aspects of this kind of truly non-equilibrium systems[2]. Because phase transitions, hysteresis effects, and other nonlinear effects of synergetics determine spatiotemporal traffic pattern features, spatiotemporal traffic phenomena may be considered an aspect of synergetics[3,4]. Different classes of spatialtemporal patterns in traffic flows can be considered as different phases of the system. Kerner[5]modeled synergetic phenomena in spatial-temporal patterns as phase transition and defined a synchronized flow phase. Phase transitions in traffic flows on multilaneroads were also studied in the framework of his threephase traffic theory proposed by Kerner and Klenov[6,7].

Microscopic approach of synergetics has been applied to model jamming transition in traffic flows based on the Lorentz system. Synergetic scheme was proposed to describe the jamming transition in traffic flows, taking into account the internal fluctuations of characteristic acceleration/braking time[8]. On the basis of Ref.[8], the influence of the characteristic acceleration/braking time in the most probable headway deviation from its optimal value was studied, and headway deviation characterizing a phase transition was showed[9]. The homotopy perturbation method, the variational iteration method[10]and the differential transformation method[11]were used to give approximations to the governing equations offered in Refs.[8,9], and these three methods could provide highly accurate analytical solutions.

Recently, the macroscopic approach of synergetics has been used to model complex social systems. The integration of the macroscopic approach of synergetics and the continuity equation was used to model residential mobility macroscopically[12]. In this paper, we attempt to use the maximum information principle, a macroscopic approach of synergetics, to calculate the velocity distribution. The feature of this method is to use the macroscopic variables of traffic flow to derive the velocity distribution, without modeling the microscopic vehicle interactions.

1. Synergetics

Synergetics is initiated by Haken[13]in 1969, which dealt with complex systems, i.e., systems composed of many individual parts that are able to spontaneously form spatial, temporal or functional structures by means of self-organization. Synergetics has formed two theoretical branches: microscopic or mesoscopic approach and macroscopic approach. For the former approach, the concepts of instability, order parameters and slaving are used, which can be cast into a rigorous mathematical form, and one could show the emergence of structures and concomitantly of new qualities at a macroscopic level. For the latter approach[14], the maximum information principle is used, which is an analogy with thermodynamics. This approach treats complex systems by means of macroscopically observed quantities, and then determines the microscopic structure of the processes which give rise to the macroscopic structure. The maximum information principle claims that the probability distribution is the most possible probability distribution when the information is maximized. In this paper, we use the macroscopic approach to study the velocity distribution evolution of traffic flow.

2. Cell transmission model

The Lighthill-Whitham-Richards (LWR) model is a first-order hydrodynamic model of traffic flows, and a macroscopic approach that provides good approximation of traffic flow evolution in realistic networks. Many numerical methods have been developed to solve related problems with the LWR model. One approach is to solve the Riemann problem by applying the Godunov method. Another approach is to use the demand and supply functions[15,16], which turns out to be a variant of the Godunov method. The third approach is the wave tracking resolution scheme[17]. The Godunov discretization scheme is efficient as it has been proved that the flow is constant during a time step. The transmission flow can be easily calculated using the following formula

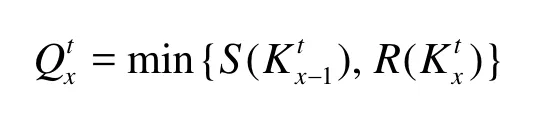
whereSandRare the demand and supply functions, respectively defined by

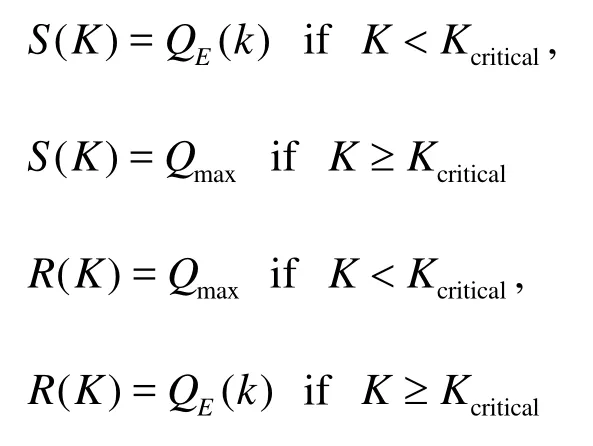
With the transmission flow, we can write the density updating formula as

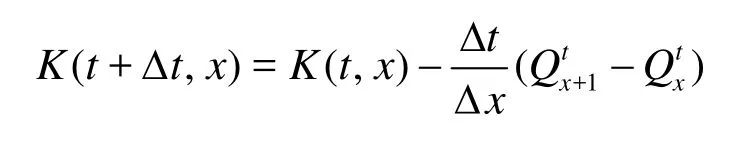
The Cell Transmission Model (CTM) transforms the differential equations in the LWR model into simple difference equations. In the CTM, a road is divided into homogeneous and interconnected segments, referred to as cells, and piecewise linear relationships are assumed between flow and density at the cell level.

3. Proposed traffic kinetic model

Let flow flux and density for traffic flow be given. We wish we could derive the probability distribution of speed. In other words, we start from the macroscopic world and wish to draw conclusions about the microscopic world. In synergetics, a measure for the amount of information is connected with the number of possible events (realizations). There is an overwhelming probability of finding that the realizedprobability distribution has the greatest possibilities, and thus the greatest amount of information. This principle has been proved to be fundamental for application to realistic systems in physics, chemistry and biology. Thus, maximum information of traffic flow means the corresponding speed probability distribution has the greatest possibilities to occur.

The objective function is to maximize the amount of information. An expression for the per information is defined as

whereiPis the relative frequency of the occurrence of possible speed.

The constraints are

Differentiating it with respect toiP, and setting the resulting expression equal to zero, we obtain

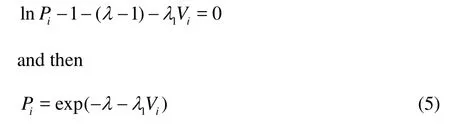
Inserting Eq.(5) into Eq.(3) leads to

which allows us to determineλonce1λis determined.

Let

Then eλ=Zorλ=lnZ. Inserting Eq.(5) into Eq.(2) gives

Taking the logarithm on its both sides

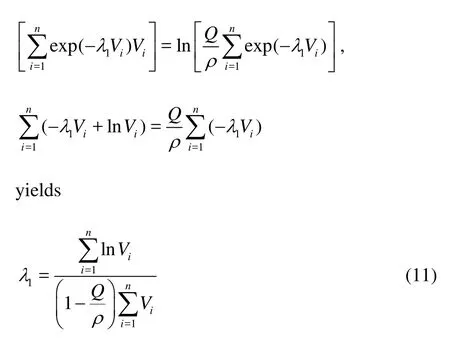
Thus, according to Eq.(11) we can calculate1λ, thenZandλ. According to Eq.(5), we can calculateiP. According to Eq.(10), we can calculateSmax.

4. Example

We simulate the speed distribution evolution for congestion spreading on the road with 1 km length using the proposed model. We discretize the road into cells with the same length of 50 m. The number of cell is twenty. The direction of traffic flow is from cell 1 to cell 20. The cell discretization is illustrated in Fig.1.

Fig.1 Cell discretization

The initial density on the road is discontinuous as follows:

The cell density is 5.35 veh/cell asx＜500 m, and the cell density is 1.95 veh/cell asx＞500 m. The initial condition shows that the first 500 m section has higher density, and traffic congestion will spread to the downstream.

The volume-density relation is

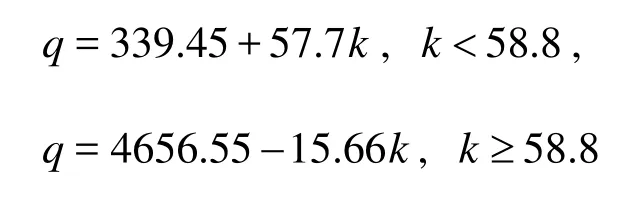
wherekis the density,qis the flow flax andxis the position. The jam density is set as 224.3 veh/km, i.e., 11.2 veh/cell.

The speed ranges from 1 km/h to 120 km/h, which are discretized into 24 classes, and the discretization step is 5 km/h. The cell 1 and cell 20 are respectively set as the source cell and the destination cell, in which the density and speed distributions remain unchanged. The number of vehicles distribution in the cell 1 and cell 20 are illustrated in Fig.2. The initial number of vehicles distribution from the cell 2 to the cell 10 is the same as the number of vehicles distribution in the cell 1. The initial number of vehicles distribution from the cell 11 to the cell 19 is the same as the number of vehicles distribution in the cell 20.

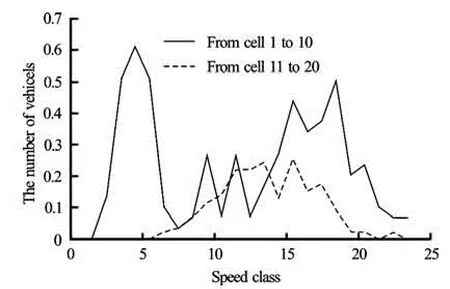
Fig.2 The number of vehicles distribution

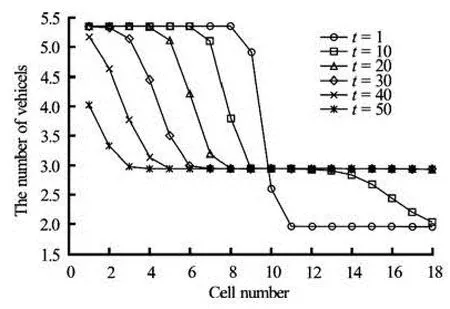
Fig.3 Cell density evolution

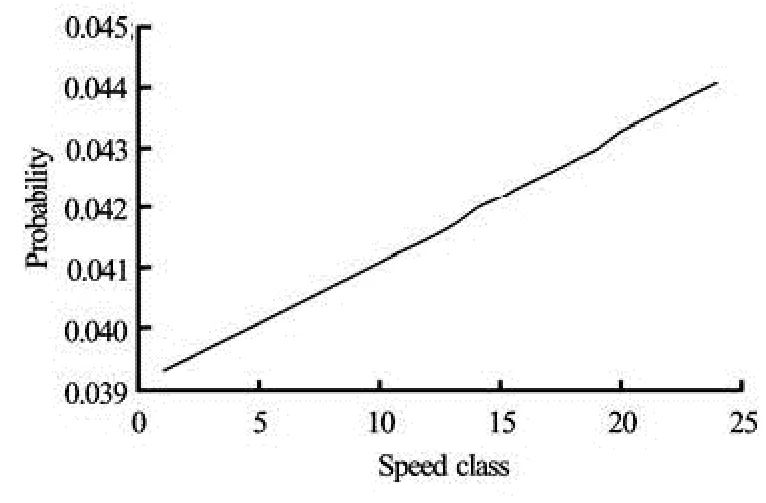
Fig.4 Speed distribution at equilibrium

The vehicle transmission between the cells is cal-culated by the CTM. The speed distribution evolution from the cell 2 to the cell 19 is calculated by the traffic kinetic model proposed in this paper. The time step is taken as 2 s. The obtained cell density evolution is illustrated in Fig.3. Discontinuous initial density evolves to an equilibrium one after some time and the density is almost the same for each cell. When traffic flow evolves to the equilibrium state, the equilibrium speed distribution is the same in each cell, which is illustrated in Fig.4. The evolution of the Lagrange multiplierλand the maximum information are respectively illustrated in Figs.5 and 6. The maximum information in cells, i.e., from the cell 2 to the cell 10, in which the initial density is high and then gradually decreases as the order number of cell density decreases. However, the maximum information for cells, i.e., from the cell 11 to the cell 19, in which the initial density is low, does not increase as the cell order increases.

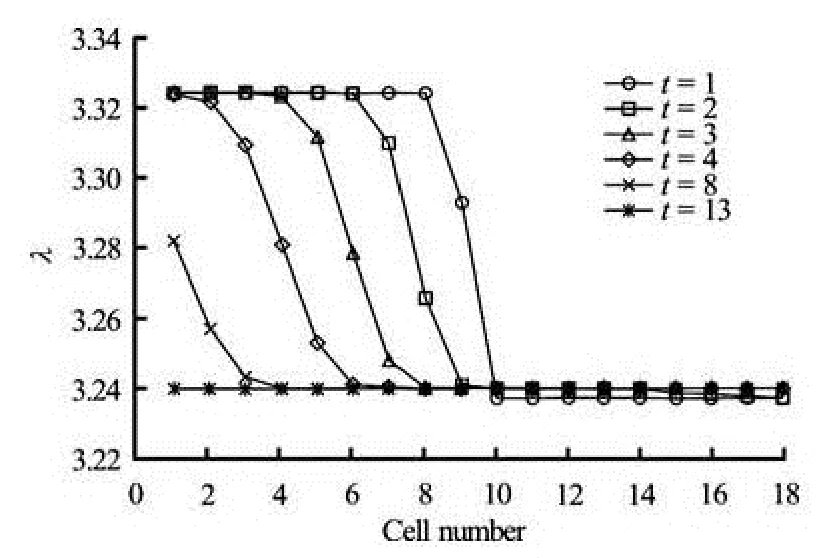
Fig.5 Evolution ofλin cells from 1 to 18

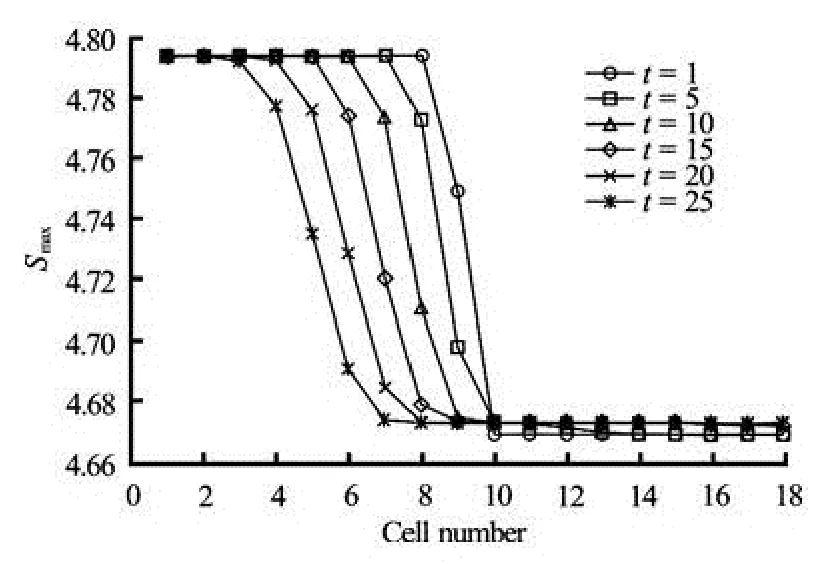
Fig.6 Evolution of maximum informationSmaxin cells from 1 to 18

5. Conclusion

In this paper, we have proposed a discrete traffic kinetic model which integrates the CTM with the maximum information principle. The presented model can deduce the speed distribution based on the macroscopic average speed, which is a better attempt to deduce the mesoscopic state from the macroscopic variables. The model provides a way to study the relation between information and traffic flow situation. An example shows the relation between maximum information and the density. As the density is higher than the critical density, the maximum information of speed distribution decreases with decreasing density. As the density is lower than the critical density, the maximum information of speed distribution remains almost unchanged for different densities.

Acknowledgement

This work was supported by the Open Fund of Key Laboratory of Road Structure and Material of Ministry of Transport, Changsha University of Science and Technology (Grant No. kfj100206).

[1] LU S., DAI S. and LIU X. A discrete traffic kinetic model-Integrating the lagged cell transmission and continuous traffic kinetic models[J]. Transportation Research Part C: Emerging Technologies, 2011, 19(2): 196-205.

[2] CHOWDHURY D., SANTEN L. and SCHADSCHEIDER A. Statistical physics of vehicular traffic and some related systems[J]. Physics Reports, 2000, 329(4-6): 199-329.

[3] KERNER B. The physics of traffic: Empirical freeway pattern features, engineering applications, and theory[M]. Berlin: Springer, 2004.

[4] KERNER B. Introduction to modern traffic flow theory and control[M]. Berlin: Springer, 2009.

[5] KERNER B. Synchronized flow as a new traffic phase and related problems for traffic flow modeling[J]. Mathematical and Computer Modelling, 2002, 35(5): 481-508.

[6] KERNER B., KLENOV S. Phase transitions in traffic flow on multilane roads[J]. Physics Review E, 2009, 80(5): 056101.

[7] KERNER B., KLENOV S. A theory of traffic congestion at moving bottlenecks[J]. Journal of Physics A: Mathematical and Theoretical, 2010, 43(42): 425101.

[8] OLEMSKOI A. I., KHOMENKO A. V. Synergetic theory for jamming transition in traffic flow[J]. Physics Review E, 2001, 63: 1-4.

[9] KHOMENKO A., KHARCHENKO D. and YUSHCHENKO O. Jamming transition with fluctuations of characteristic acceleration/braking time[J]. Bulletin of Lviv University, 2004, 37: 44-56.

[10] GANJI S. S., BARARI A. and NAJAFI M. et al. Analytical evaluation of jamming transition problem[J]. Canadian Journal of Physics, 2011, 89(6): 729-738.

[11] GANJI S. S., BARARI A. and IBSEN L. B. et al. Differential transform method for mathematical modeling of jamming transition problem in traffic congestion flow[J]. Central European Journal of Operations Research, 2012, 20(1): 87-100.

[12] RAJARAM R., CASTELLANI B. Modeling complex systems macroscopically: Case/agent-based modeling, synergetics, and the continuity equation[J]. Complexity, 2012, 18(2): 8-17.

[13] HAKEN H. Synergetics, Introduction and advancedtopics[M]. New York: Springer, 2004.

[14] HAKEN H. Information and self-organization: A macroscopic approach to complex systems, third enlarged edition[M]. New York: Springer, 2006.

[15] DAGANZO C. F. The cell transmission model: A dynamic representation of highway traffic consistent with the hydrodynamic theory[J]. Transportation Research B, 1994, 28(4): 269-287.

[16] LEBACQUE J. P. The Godunov scheme and what it means for first order traffic flow models[C]. Proceedings of the 13th International Symposium on Transportation and Traffic Theory. Lyon, France, 1996, 647-677.

[17] HENN V. Wave-based resolution scheme for the hydrodynamic LWR traffic flow model[C]. Proceedings of Traffic and Granular Flow’03. Delft, The Netherlands, 2005, 105-124.

10.1016/S1001-6058(13)60418-7

* Project supported by the National Natural Science Foundation of China (Grant No. 71071024), the Hunan Provincial Natural Science Foundation (Grant No.12JJ2025).

Biography: LIU Xi-min (1980-), Female, Ph. D. Candidate, Lecturer

LU Shou-feng,

E-mail: itslusf@gmail.com