高勤潘

1 预备知识

1.1 研究背景，意义及方法

Ramsey 数的问题是最重要的一类极值问题。由于此类问题的重要意义和它的困难程度引起图论界的高度重视，很多优秀的数学家投身其中，在解决许多棘手问题的同时，引入了很多巧妙的方法。但是能够准确知道的 Ramsey 数值为数极少，每一个准确数值的获得都具有不可估量的理论和实践意义。而且大多数的上界和下界都没有被得出。代数的方法使得许多图的构造美观而实用。构造的图中，许多Ramsey 数的下界可以得到；而且，矩阵的代数方法提供了多元数组，为图中公共邻点个数等有力的帮助。分析方法甚至微分方程的方法和一些半随机思想利用独立集等解决Ramsey 数性质，分析解决问题的思路。概率的方法提供的概率空间证明了看似不存的性质的存在性，随机图，概率空间为Ramsey 数的下界等提供了经典的证明。

1.2 图的概念和性质

图G的顶点的个数成为图G的阶数，记为|G|；它的边数记为‖G‖，通常考虑的图都是有限图。点v和边e是关联的，如果v∈e，那么e是点v上的一个边，两个点和同一条边关联时，一个点称为始点，一个称为终点。一条边{x;y}通常简记为xy或者yx。如果图G中所有的顶点之间都有边，则称图G是一个完全图。一 个n阶完全图记为Kn。一个各部分的阶数分别为：n1,…，nk的k部完全图记为：K(n1,…,nk)，而且如果对每个1≤i≤k有nn=n，则简记为：Kk(n)；完全二部图K(t,s)可简记为Kt,s。图K1,s称为一个星图。若n个顶点依次连接构成一个通道，则称它为路径Pn，若该通道首尾相连，则称它为圈Cn。如果U是图G中任意一个点集，我们把G[VU]记为G-U。换句话说，G-U是在图G中删去集合U∩V中的点以及和这些点相邻的边儿得到的。G=(V;E)是一个非空图，图G中点v的所有邻点的集合记为NG(v)或者直接简记为N(v)。更一般的，对于U⊆V，集合VU中所有的集合U中点的邻点称为集合U的邻点，记为N(U)。点v的度数dG(v)=d(v)就是在点v的边|E(v)|的个数，根据我们对图的定义，它等于点v的邻点的个数。若对于图的边有红蓝着色，那么在顶点v的邻点中，蓝色，红色的分别记为dB(v),dR(v)。若顶点集W∈V(R),记作dB(v,W)=|NB(v)∩W|。度数为0 的点称为独立点。数值δ(G)=min{d(v)|v∈V}称为图G的最小度，数值Δ(G)=max{d(v)v∈V}称为图G的最大度。如果图G的所有点有相同的度数k，那么我们就说图G是 正则的，或者简单的称为正则的，记为k-正则图。扇形图Fn=K1+nK2是指一个中心点有n个相连的扇叶，每个扇叶是两个相连顶点。因此，Fn是n个三角形共用 1 个顶点。车轮图Wn=K1+Cn的定点个数为n+1，它由长为n的圈上的每个顶点与额外一个顶点相连。

2 主要结果

2.1 引理1及证明

引理1 若n为大于10 的偶数，图R是一个顶点为2n+1的n-正则图, 记B为R的补图。则或者R包含F2,或者B包含Wn。

证明假设R不包含F2, 则任意顶点x的邻点N(x)的子图不包含2K2。那么,N(x)诱导一个三角形，或者一个空图，或者一个星形图。记N(x)={v1,v2,…,vn},NB(x)={u1mu2,…,un}.那么{x},N(x),NB(x)构成了所有顶点V(R)。对于任意顶点v∈V(R)和顶点集W∈V(R), 我们记dB(v,W)=|NB(v)∩W| 。

情形1N(x)中所有的边诱导一个K3，不妨记为{v1,v2,v3}。因为R是n-正则的,{v1,v2,v3}中的每个顶点与NB(x)中的n-3个顶点相连。由于3(n-3)>n因此至少存在一个顶点u∈NB(x)与{v1,v2,v3}中的两个点相连。因此{u,v1,v2,v3,x}构成了一个R中的F2。 与假设矛盾。

情形2N(x)中所有边诱导一个空图或者星图K1,1。我们可以得到任意u∈NB(x)满足dB(u,N(x))≤2(否则dB(u,N(x))≥3,B中存在一个顶点集为{u,v1,v2,v3,…,vn}的Wn)。注意到B也是n-正则的，因此dB(u,NB(x))≥n-3≥n/2.所以NB(x)在B中包含一个Cn, 此时Cn∪{x}构成了B中的Wn。

情形3NR(x)中的所有边诱导一个星图K1,m(m≥2) 。假定这个星形图中心为v1,记V1={v2,v3,…,vm+1} 为星图中度数为 1 的点集，NR(x)中其他点为V2={Vm+2,vm+3,…,vn}.显然，{v2,v3,…,vn}诱导了一个B中的Kn-1。

情况3.1 2≤m≤n-5。那么，v2∈V1在NB(x)中恰好有n-2个邻点，记这些点的点集为U′。若U′包含一条边usut,则{us,ut,v2,v1,x}就会构成一个以v2为中心的F2。所以U′构成了B中的一个Kn-2。记u1,u2为NB(x)中不在U′里的两个顶点，那么dB(ui,N(x))≤m+1,i=1,2.(否则B就会有Wn以{ui,v1,v2,…,vn}为顶点集,i是1或者2)。

所以,dB(ui,NB(x))≥(n-1)-(m+1)≥3,i=1,2.如果B中u1,u2均与U′中一个顶点相连,不妨记为u3, 那么 我们得到顶点集{u3,x,u1,u2,…,un}上以u3为中心的Wn。否则, 我们得到顶点集{x,u1,u2,…,un}上以x为中心的Wn。

情况3.2n-4≤m≤n-2.我们仅证明m=n-4的情况(其他情况同理)。

所以，dB(ui,U″)≤3,i=1,2.(否则，B中会有一个以{x,ui,vi}∪U″为顶点的Wn)。

又因为dR(vi,NB(x))=n-1,i=n,n-1,n-2，所以在R中，至少存在一点u∈U″是u1,u2,vn,vn-1,vv-2公共交点(n>10)，即

高职教育是一种跨界教育，教师核心素养和能力的培养需要“政校行企”四方的联合培养，学校和企业需要参与教师的培养，在监督方面存在一定嫌疑。对此，行业应该发挥出考核官的作用，有效地监督高职院校教师核心素养和能力建设的情况。目前，随着教学改革以及人才培养需求的不断提升，高职院校的校企合作工作有了一定的进展，不断完善合作过程中的各种细节。然而，对高职教师核心素养和能力建设监督方面，行业并没有起到明显的监督作用。行业发展规划中并没有涉及职业教育教师能力的培养，缺乏对教师核心素养、能力和行业人才教育之间关系的梳理。行业应该把高职院校教师核心素养和能力作为企业认证的重要指标之一，加大校企双方合作的力度。

dR(u)≥(n-4)+5=n+1。这与R是n-正则图矛盾。

情况3.3m=n-1. 这种情况，B中顶点v1与NB(x)中所有顶点相连。由上述情况知，对于2≤i≤n，NB(vi)∩NB(x)是相同的顶点集，记为U″={u3,u4,…,un}。类似的，可以得出，dB(ui,U″)≤1,i=1,2.(否则，B中会有一个以{x,u,v1}∪U″为顶点的Wn)。所以在R中，至少存在一点u∈U″是u1,u2的公共点，即dR(u)≥(n-1)+2=n+1，这与R是n-正则图矛盾。

2.2 引理2及证明

引理2 对于任意正整数s，t，且t≥2x.那么R(Wt,sK2)-s+t。

证明由于Kt∪Ks-1不包含子图Wt，而且它的补图也不含有sK2,显然R(Wt,sK2)≥s+t.

现在证明R(Wt,sK2)≤s+t即可。对s作归纳法。当s=1时，不等式显然成立。假定s≥2，并且不等式对于小于 的正整数成立，即R(Wt(s-1)K2)≥s+t-1.因此,对Ks+t做红蓝边着色，若没有红色的Wt出现，则必定含蓝色的(s-1)K2。假设没有蓝色sK2出现，我们用U={u1,v1,u2,v2,…,us-1,vs-1}表示构成蓝色(s-1)K2的顶点集, 其中uivi是相互独立的蓝边,i=1,2,…,s-1.令V=VU，则|W|=t-s+2.显然W诱导了一个红色Kt-s+2,否则W就会包含一条蓝边, 这条蓝边和U构成蓝色sK2。

如果vi和W中的一个顶点相连的边是蓝边,那么ui一定和W中的其他顶点的边是红色的，否则我们可以得到ui,vu和W之间两条独立的蓝边，进而形成一个蓝色sK2。为标记方便，我们记每个ui至多和W中一个顶点蓝色相连.如果存在这样和ui蓝色相邻的点，记为ηi；记W中所有这样的ηi构成集合η。则

|η|≤s-1

|Wη|≥(t-s+2)-(s-1)=t-2s+3≥1

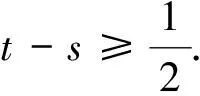
综上，证明完毕。

2.3 定理3及证明

定理3 若n是大于10 的偶数，且Δ(G)≤n，|G|=2n+1，则或者G包含Wn，或者G的补图包含F2。

证明考虑一个红蓝边着色的完全图K2n+1，记R和B分别为包含所有红边和蓝边的子图。下面证明或者存在一个红色的F2或者一个蓝色Wn。Δ(B)≤n时，B即为定理中的图G。下面转化为证明：当蓝边最大度不超过n时，B中含蓝色Wn，或者R中含红色F2。

情形1 红边最大度大于n+1。即存在一个顶点x,dR(x)≥n+2。又R(Wn,2K2)=n+2，由引理 2，即x的这些邻点构成的子图包含红色的2K2或蓝色Wn，则或者存在红色的F2或者一个蓝色Wn。

情形2 红边最大度为n+1。此即存在一个顶点x,dR(x)=n+1。由情形 1，我们现在考虑所有定点的绿边至少为n-1。如果NR(x)诱导一个2K2, 结论显然成立；因此我们假定NR(x)没有2K2，那么NR(x)或者没有红边, 或者诱导一个红色星型图，或者一个红色三角形。

情况2.1NR(x)没有红边。这种情况NR(x)诱导了一个蓝色的Kn+1,即包含了一个蓝色Wn。

情况2.2NR(x)诱导了一个红色星形图K1,m。记NR(x)={v1,v2,…,vn+1},其中v1是星形图K1,m的中心,记NB(x)={u1,u2,…,un-1}。

当1≤m≤n-3时,NR(x)中容易发现一个蓝色Wn，这是因为{v2,…,vn+1}诱导一个蓝色Kn, 而且v1至少与{v2,…,vn+1}中三个顶点的边为蓝色，因而它们构成一个蓝色的Wn。

现在考虑m=n-2时的情况(同理可得m=n-1或n的情况)。记v1v2,…,v1vn-1为红边，v1vn,v1vn+1为蓝边。由于v1至多有n+1个红邻点, 那么在NB(x)中v1至多与两个点的边为红色, 因此它至少与NB(x)中n-3个顶点的边为蓝边。{v2,…,vn+1}诱导了蓝色的Kn, 因此任何顶点u∈NB(x)至多与{v2,…,Vn}两个顶点的边为蓝色，与其余顶点均连红边(否则就会有蓝色Wn在{u,v2,…,vn+1}中)。所以，NB(x)中任意us和ut在{v2,…,vn-1}中有公共邻点构成红边，即NB(x)诱导一个蓝色Kn-1(否则NB(x)中存在一条红边的端点us和ut在{v2,…,vn-1}中有公共邻点，不妨记为v，进而在{us,ut,v,v1,x}中存在 以v为中心的红色F2).又因为在NB(x)中v1与至少n-2≥3个顶点连蓝边，在此基础上，我们得到一个以NB(x)∪{x,v1}为顶点的蓝色Wn。

情况2.3NB(x)中所有边的点诱导一个红色三角形, 这意味着NR(x)诱导了一个 边为Kn+1减去一个三角形的图, 显然这个图包含Wn。

情形3 红边最大度不超过n。因为蓝边最大度不大于n，所以R与B均为n-正则的。由引理 1，命题成立。

综上，命题得证。

[参 考 文 献]

[1] S.Burr.Ramsey numbers involving graphs with long suspended paths[J]. London Math.Soc,1981:405-413.

[2] Y.Li,C.Rousseau. Fan-complete graph Ramsey numbers[J].Graph Theory, 1996:413-420.

[3] A.Salman,H.Broerma. Path-fan Ramsey numbers.Discrete Appl[J].Math,2006(154):1429-1436.

[4] R.J.Faudree,J.Schelp. All Ramsey numbers for cycles in graphs[J].Discrete Math,1974(8):313-329.

[5] B.Bollobas.Extremal Graph Theory[M].New York:Academic Press,1978.

[6] Surahmat et al. The Ramsey numbers of large cycles versus wheels[J].Discrete mathematics，2006(306):3334-3337.

[7] H.-L.Zhou.On book-wheel Ramsey number[J].Discrete mathematics,2000(224):239-249.