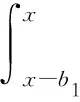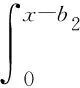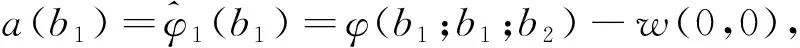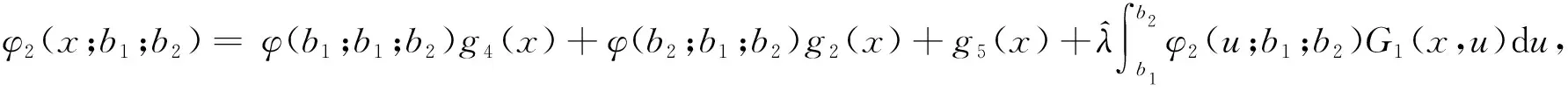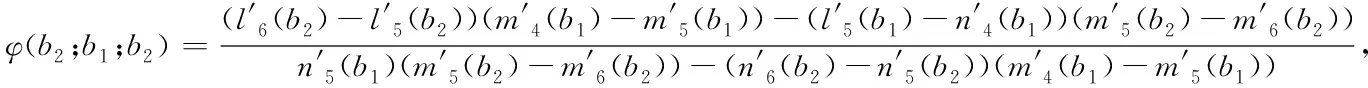The Compound Poisson Risk Model Perturbed by Diffusion with Double-Threshold Dividend Barriers to Shareholders and Policyholders
2012-11-22ZHOUJiemingOUHuiMOXiaoyunYANGXiangqun
ZHOU Jie-ming, OU Hui, MO Xiao-yun,2, YANG Xiang-qun
(1.Key Laboratory of High Performance Computing and Stochastic Information Processing (Education Ministry of China), College of Mathematics and Computer Science, Hunan Normal University, Changsha 410081, China;2.Department of Basic Course, Hunan University of Finance and Economics, Changsha 410205, China)
1 Introduction
The classical risk model perturbed by a diffusion was first introduced by Gerber[1]and has been further studied by many authors during the last few years (see [2~5] and the references therein).
Dividend strategy for insurance risk models first proposed by De Finetti[6], various barrier strategies have studied by many authors, including [7~12]. Among them Albrecher and Kainhofer[7], Albrecher et al[8]discussed the non-linear dividend barrier, Gerber and Shiu[9], Lin and Pavlova[10]studied the threshold dividend strategy in the classical risk model. He and Yang[11]investigated the compound binomial model with randomly paying dividends to shareholders and policyholders. Wan[12]considered the classical risk model perturbed by a diffusion with a threshold dividend strategy.
In this paper, we extend the model [12], and consider a joint stock insurance company which pays dividends to shareholders and policyholders on the compound Poisson risk model perturbed by diffusion: given two thresholds, the company decides to pay dividends to sharcholders and policyholders according to the current surplus level. In Section 2, the model assumptions are formulated; In Section 3, integro-differential equations for the expected discounted dividend payments prior to ruin are derived and closed-form solutions are given; The explicit formulas for the Gerber-Shiu expected discount penalty function are obtained in Section 4.
2 The model
Let (Ω,F,Ft,P) be a field probability space satisfying the usual conditions, containing all objects defined in the following. In the perturbed compound Poisson risk model, the surplus of an insurer has the form
(1)
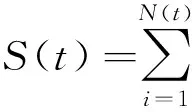
We consider the following extension of model (1). We assume that the company pays dividends according to the following strategy governed by parametersb2>b1>0 andα1>0,α2>0. When the modied surplus is below the levelb1, no dividends are paid; when the modied surplus is between the levelb1andb2, dividends are paid continuously for its policyholders at a constant rateα1; when the modied surplus is above the levelb2, the company will pay dividends to its shareholders at rateα2(of course, must pay dividends to its policyholders at rateα1). Thus, the dynamics of surplus processX(t) are given by
(2)
The time of ruin for risk process (2) is defined asTb1,b2=inf{t≥0:X(t)≤0} with inf{∅}=∞. Fort≥0, letδ>0 be the force of interest, whereD(t) denotes the aggregate dividends paid by timet, and letDx,b1,b2denotes the present value of all dividends until time of ruinTb1,b2,
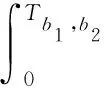
Forx≥0, we use the symbolV(x;b1;b2) to denote the expectation ofDx,b1,b2,
V(x;b1;b2)=E[Dx,b1,b2|X(0)=x].
Define the Gerber-Shiu expected discounted penalty functionφ(x;b1;b2) by
φ(x;b1;b2) =E[e-δTb1,b2w(X(Tb1,b2-),|X(Tb1,b2)|)I(Tb1,b2<∞)|X(0)=x],
(3)
whereX(Tb1,b2-) is the surplus immediately before ruin, |X(Tb1,b2)| is the deficit at ruin andw(x1,x2) is an arbitrary non-negative function on [0,∞)×[0,∞).δ≥0 may be interpreted as the force of interest.
3 The expected discounted dividend payments
In this section, we will give the integro-differential equations and the renewal equations satisfied by the expected discounted dividend paymentsV(x;b1;b2), then its closed-form solutions.
Clearly,V(x;b1;b2) behaves differently with different initial surplus. For notational convenience, we set
Then we have
Theorem1For 0 (4) forb1≤x (5) forb2≤x< ∞,V(x;b1;b2) satisfies the following nonhomogeneous integro-differential equation (6) ProofLetT1denote the time of first claim andZ1be the amount of the first claim. Consider the infinitesimal interval from 0 to dt. Conditioning, one obtains that when 0 V1(x;b1;b2)=e-δdtP(T1>dt)E[V1(x+cdt+σW(dt);b1;b2)]+ e-δtP(T1≤dt)E[V1(x+cdt+σW(dt)-Z1;b1;b2)]; (7) whenb1≤x V2(x;b1;b2)=e-δdt{α1dt+P(T1>dt)E[V2(x+(c-α1)dt+σW(dt);b1;b2)]+ P(T1≤dt)E[E[V2(x+(c-α1)dt+σW(dt)-Z1;b1;b2)|Z1∈(0,x+(c-α1)dt+ σW(dt)-b1)]+E[V1(x+(c-α1)dt+σW(dt)-Z1;b1;b2)|Z1∈(x+(c-α1)dt+ σW(dt)-b1,∞)]]}; whenb2≤x<∞, V3(x;b1;b2)=e-δdt{(α1+α2)dt+P(T1≥dt)E[V3(x+(c-α1-α2)dt+σW(dt);b1;b2)]+ P(T1≤dt)E[E[V3(x+(c-α1-α2)dt+σW(dt)-Z1;b1;b2)|Z1∈(0,x+(c-α1-α2)dt+ σW(dt)-b2)]+E[V2(x+(c-α1-α2)dt+σW(dt)-Z1;b1;b2)|Z1∈(x+(c-α1-α2)dt+ σW(dt)-b2,x+(c-α1-α2)dt+σW(dt)-b1)]+E[V1(x+(c-α1-α2)dt+σW(dt)- Z1;b1;b2)|Z1∈(x+(c-α1-α2)dt+σW(dt)-b1,∞)]]}. Since e-δdt=1-δdt+o(dt),P(T1>dt)=1-λdt+o(dt) andP(T1≤dt)=λdt+o(dt). Then by Taylor’s expansion, we have wherex*∈(x,x+cdt+W(dt)). By the assumption thatW(t) is a standard Brownian motion in model (1), we haveE[W(dt)]=E[W3(dt)]=0 andE[W2(dt)]=Var[W(dt)]=dt. Then, we can obtain Submit the above equation into (7), and letting dt→0, we get the integro-differential equation (4). Now, one can obtain equations (5) and (6) by some simple calculations. V1(b1-;b1;b2)=V2(b1+;b1;b2)=V(b1;b1;b2), (8) V2(b2-;b1;b2)=V3(b2+;b1;b2)=V(b2;b1;b2), (9) (10) (11) By the similar approach to (2.5) and (2.6) in [12] we can prove that (8)~(11) hold. For 0 (12) From (85) in the Appendix, we have (13) where The above expression (13) can be rewritten as V1(x;b1;b2)=V1(b1-;b1;b2)m1(x)=V(b1;b1;b2)m1(x), (14) Forb1≤x (15) From (86) in the Appendix, we have (16) where andg1(x),g2(x) are defined as (69) and (70)in the Appendix, respectively. Then, the above expression (16) can be rewritten as V2(x;b1;b2)=V(b1;b1;b2)m2(x)+V(b2;b1;b2)n2(x)+l2(x), (17) where Then, we have (18) (19) (20) (21) where Submitting (20) into (21), we can obtain (22) So by iteration, we have (23) where The above expression (23) can be rewritten as V3(x;b1;b2)=V(b1;b1;b2)m3(x)+V(b2;b1;b2)n3(x)+l3(x), (24) where Then, we have (25) In view of the continuity condition (10) and (11), by (14), (18), (19) and (25), we have (26) (27) Thus according to (12)~(27), we obtain the following theorem. Theorem2The expected discounted dividend paymentsV(x;b1;b2) can be written as the following closed-form: whereV(bi;b1;b2);i=1,2,mj(x),j=1,2,3,nk(x),lk(x),k=2,3 are defined as above, respectively. In the following we will discuss the famous Gerber-Shiu expected discounted penalty function under the risk model (2). The expected discounted penalty functionφ(x;b1;b2) is defined as (3) in Section 2. Clearly, the expected discounted penalty functionφ(x;b1;b2) behaves differently with different initial surplusx. Here for notational convenience, we write By similar derivation to (4)~(6), we can get the following theorem. Theorem3For 0 forb1≤x forb2≤x<∞,φ(x;b1;b2) satisfies the following integro-differential equation: with the boundary conditions φ1(0;b1;b2)=w(0,0), (28) (29) φ1(b1-;b1;b2)=φ2(b1+;b1;b2)=φ(b1;b1;b2), (30) φ2(b2-;b1;b2)=φ3(b2+;b1;b2)=φ(b2;b1;b2), (31) (32) (33) If the initial surplusx=0, then ruin is immediate, i.e.,Tb1,b2=0, soX(Tb1,b2-)=0 and |X(Tb1,b2)|=0, thus (28) holds; ifX(0)→∞, ruin does not happen all the time, henceTb1,b2=∞ and (29) holds. Similar approach to (3.6) and (3.7) in [12], we can prove that (30)~(33) hold. For 0 (34) (35) whereF(x) is defined as (51) in the Appendix. Submitting (34) into (35), we can obtain By iteration, we have φ1(x;b1;b2)=φ(b1;b1;b2)m4(x)+n4(x), (36) (37) (38) whereG1(x,u),G2(x,u) andFα1(x) are defined as (62), (63) and (66) in the Appendix, respectively. Submitting (36) into (38), we can obtain (39) φ2(x;b1;b2)=φ(b1;b1;b2)m5(x)+φ(b2;b1;b2)n5(x)+l5(x), (40) (41) (42) (43) whereG3(x,u),G4(x,u) andFα1,a2(x) are defined as (77),(78) and (79) in the Appendix, respectively. Submitting (36), (40) into (43), we can obtain (44) where By iteration, we have φ3(x;b1;b2)=φ(b1;b1;b2)m6(x)+φ(b2;b1;b2)n6(x)+l6(x), (45) where Then, we have (46) In view of the continuity condition (32) and (33), by (37), (41), (42) and(46), we have (47) (48) According to (36)~(48), we can obtain the following theorem. Theorem4The expected discounted penalty functionφ(x;b1;b2) can be written as the following explicit formulas whereφ(bi;b1;b2),i=1,2,mj(x),nj(x),j=4,5,6,lk(x),k=5,6, are defined as above, respectively. Appendix In this section, we will show that three kinds of integro-differential equations such as (4), (5) and (6) are identical to the following three renewal equations in details and show that the solutions of integro-differential equations are unique. Based on these, their closed-form solutions are obtained. Theorem5The integro-differential equation (49) is identical to the renewal equation (50) (51) (52) (53) andK(x,y) is defined by (55) and (56). ProofLetK(x,y) be the solution of the following equation, (54) Then we can solve (54) explicitly, (55) where (56) C2(x)=-C1(x)e(β1-β2)b1, Let (57) ThenW(x) satisfies the equation (58) wheref1(x) is defined as (53). Multiplying both sides of the Eq.(58) byK(x,y) and integrating from 0 tob, integration by part and in view of (54), we get (59) and substituting (57) into (59), we get whereF(x) is defined in (51). Thus the theorem holds. Theorem6The integro-differential equations (60) is identical to the renewal equation (61) (62) (63) (64) (65) (66) (67) (68) (69) (70) (71) Then we can solve (71) explicitly, where Let W(x)=v2(x)-a1(b1)θ1(x)-a2(b2)θ2(x), (72) whereθ1(x) andθ2(x) are defined in (64) and (65). ThenW(x) satisfies the equations (73) whereg01(x),g02(x) are defined as (67) and (68). (74) Substituting (72) into (74), we get whereFα1(x) is defined in (66). Thus the theorem holds. Theorem7The integro-differential equation (75) is identical to the renewal equation (76) (77) (78) (79) (80) (81) Then we can solve (81) explicitly, Let W(x)=v3(x)-a3(b2)eb2-x, (82) thenW(x) satisfies the equations (83) whereh1(x) is defined as (80). (84) Substituting (82) into (84), we get whereFα1,α2(x) is defined in (79). Thus we show that the theorem holds. Next we will show that the solutions of equations (49), (60) and (75) are unique using the similar method as in [12] and [13]. The same results can be obtained for other integro-differential equations. Hence, by iteration, we can get the closed-form solutions of (49), (60) and (75) from (50), (61) and (76), (85) (86) (87) : [1] GERBER H U. An extension of the renewal equation and its application in the collective theory of risk[J]. Skandinavisk Aktuarietidskrift, 1970,1970(3-4):205-210. [2] CHIU S N, YIN C C. The time of ruin, the surplus prior to ruin and the deficit at ruin for the classical risk process perturbed by diffusion[J].Insurance:Math Eco, 2003,33(1):59-66. [3] DUFRESNE F, GERBER H U. Risk theory for the compound Poisson process that is perturbed by diffusion[J].Insurance:Math Eco, 1991,10(1):51-59. [4] TSAI C C L, WILLMOT G E. On the moments of the surplus process perturbed by diffusion[J].Insurance:Math Eco, 2002,31(3):327-350. [5] WANG G, WU R. Some distributions for classical risk processes that is perturbed by diffusion[J].Insurance:Math Eco, 2000,26(1):15-24. [6] DE FINETTI B. Su un’impostazione alternativa dell teoria colletiva del rischio[J]. TransaXVInt Congress Actuaries, 1957,2:433-443. [7] ALBRECHER H, KAINHOFER R. Risk theory with a non-linear dividend barrier[J].Computing, 2002,68:289-311. [8] ALBRECHER H, KAINHOFER R, TICHY R F. Simulation methods in ruin models with non-linear dividend barriers[J].Math Comput Simul, 2003,62(3-6):277-287. [9] GERBER H U, SHIU E S W. On optimal dividend strategy in the compound Poisson model[J].North Americal Actuarial, 2006,10(2):76-93. [10] LIN X S, PAVLOVA K P. The compound Poisson risk model with a threshold dividend strategy[J].Insurance: Math Eco, 2006,38(1):57-80. [11] HE L, YANG X Q. The compound binomial model with randomly paying dividends to shareholders and policyholders[J]. Insurance: Math Eco, 2010,46(3):443-449. [12] WAN N. Dividend payments with a threshold strategy in the compound Poisson risk model perturbed by diusion[J]. Insurance: Math Eco, 2007,40(3):509-523. [13] LUO J. The pricing theory and the application of the American options and the numerical algorithm of the implied volatility[D]. Shanghai: Fudan University, 2005.
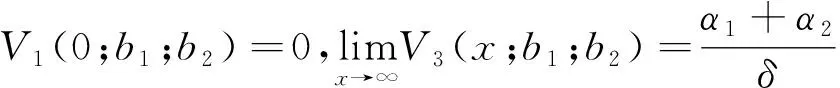
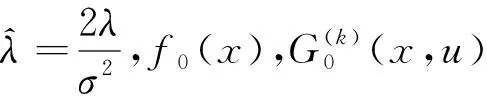
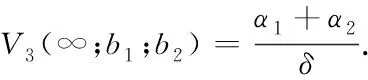
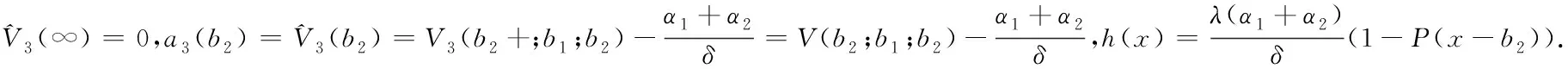
4 The Gerber-Shiu expected discounted penalty function