形变分析中的模型精化研究

2012-09-22胡杰

城市勘测 2012年6期

胡杰

(广东省电力设计研究院，广东广州 510663)

1 前言

现代测量数据处理中，影响观测值取值的因素很多，大概分为两部分:一部分为已知函数部分，作为参数分量;另一部分为某些干扰因素，同观测量的关系是完全未知的，可以将其看作非参数分量，即用非参数分量表达参数模型表达不完善的部分。

在我们建立数学模型时往往无法考虑到所有因素。为处理方便，常选择较为简单的函数来代替。因此，平差建立的函数模型只是实际的近似描述，即存在模型误差。当模型误差与偶然误差相比是一个微小量时，可以忽略模型误差。而当模型误差较大时，就会对参数估值产生较大影响，甚至会产生错误结论［2］。

本文详细分析两种将参数和非参数模型进行组合的混合模型算法，即“基于时间序列的半参数回归分析法”和“基于线性回归的神经网络精化法”。

2 参数模型和非参数模型

参数回归模型对回归函数提供大量信息，当假设的模型成立时，未知数解具有较高精度。但由于回归函数的形式假设是已知的，只是参数待定，所以回归形式一旦固定就相对呆板，往往回归效果差。非参数回归与参数回归则正好相反，它的回归函数形式是任意的，不拘束于观测量的分布限制，具有很强的适应性。但实际上对拟合函数不作任何限制是不可能的，在非参数回归方法中，无论最近邻法、核函数法、样条函数法都存在参数选择的问题，这也是非参数回归模型的难点。

2.1 参数回归模型

假设对(L，X)作 n 次等精度观测(Li，Xi)，i=1，2，…，n，则有:

式中:B为列满秩矩阵;X为参数向量;△为随机误差项。

2.2 非参数回归模型

参数模型中，观测值是未知参数的线性函数，从而要求数据处理中提供大量额外信息，由于参数模型的局限性，数学界提出了非参数模型，如下所示。

假设(Yi，Xi)，i=1，2，…，n，满足:

{εi}服从 E(εi)=0独立同分布，{Xi}可以是随机的或非随机。一般情况下，只考虑非随机的情况，也就是说，回归函数g(X)的估计n(X)总可以表示为如下形式:

在一般实际问题中，权函数满足下述条件:

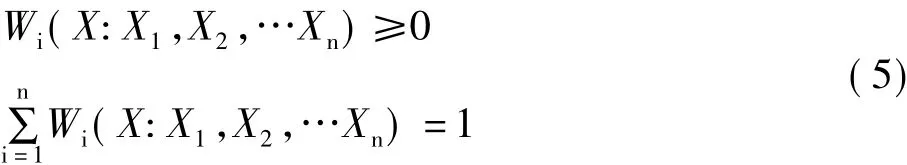
满足上述条件的权函数为概率权。不同的权函数形式产生了不同的估计方法。由于对y=g(x)的具体形式没有作任何假设，这个模型比参数模型具有更大的适应性。然而非参数模型无法利用经验或试验资料提供的这些信息，明显降低了模型的解释能力。

3 组合模型

通过以上分析，我们考虑如何兼顾参数模型和非参数模型的优点，对现有数据分析模型进一步精化，从而较单纯的参数模型或非参数模型有更大的适应性，并具有更强的解释力，更接近于真实。接下来就详细介绍两种精化模型，即“基于时间序列的半参数回归分析法”和“基于线性回归的神经网络精化法”。

3.1 基于时间序列的半参数回归分析法

半参数回归模型由参数部分和非参数部分共同组成，在测量中的应用处于探索的阶段，目前主要是通过构造正规化矩阵和平滑参数，利用补偿最小二乘法获取参数和非参数解。

在半参数模型中，平滑参数主要利用交叉核实法确定。由于变形观测值是以一定的时间序列为基础，若假设相邻时刻的模型误差si与si+1的差别不应太大。因此可令，此时可以选择如下形式的正则化矩阵:

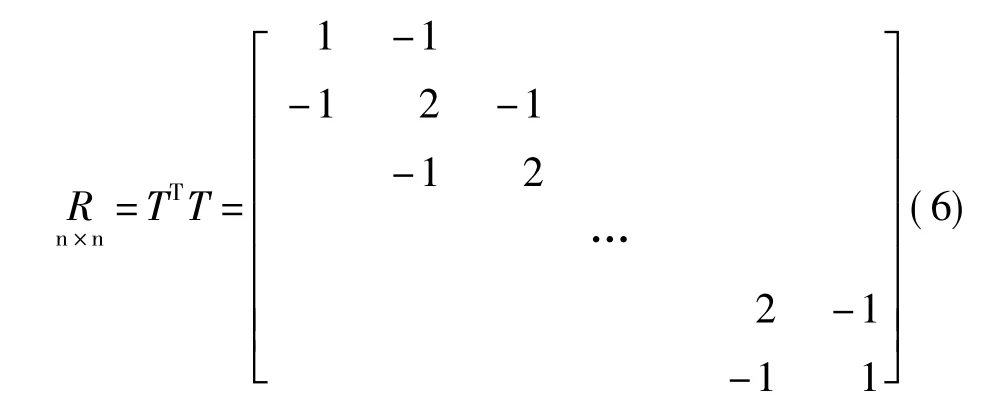
这时因rank(R)=n－1＜n，即R秩亏，还需再增加一个约束条件。若进一步假设S呈周期性变化，观测值分布均匀，个数足够，则可令，增加这一约束条件可以解决秩亏的问题。利用时间序列法由上式选择的正则化矩阵R，在实践中得到了较为广泛的应用。

于是平差问题归结为下述条件极值问题:

同样来构造拉格朗日函数:

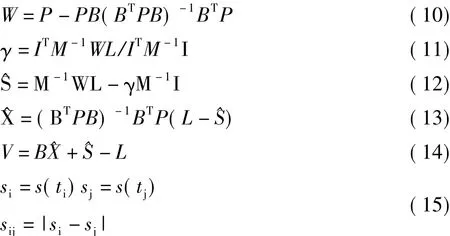
3.2 基于线性回归的神经网络精化法

在形变分析中，我们可以把变形序列看成由趋势项、周期项和观测误差三部分组成。趋势项利用经典最小二乘法求解。其他部分可以利用神经网络去映射。神经网络算法强大的自学习功能，在模型精化过程中，既弥补前述精化模型的不足，又没有人为假设所产生的误差，在理论上这样能得到较好的效果［7］。

3.2.1 基于神经网络的精化模型

变形观测的每期数据属于独立观测值，所以可以看作等精度观测值来讨论函数模型的精化方法。精化模型为:

式中:A为列满秩矩阵;X为参数向量;G为模型的精化部分;△为随机误差项。

在此模型中参数X起解释模型物理意义的作用，而G起对趋势模型修正的作用。实质上G也是参数X和观测值L的函数，即

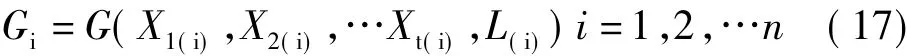
只是它们之间的关系是隐含的，通过神经网络得到它的显式数值表示。这样利用神经网络使得式(16)的模型既具有物理意义，又达到比较理想的精度。

3.2.2 参数X的估计

利用变形观测的n次观测数据，选定根据实际问题所采用的线性回归模型，在最小二乘准则下，可得X最优无偏估计^X为

3.2.3 参数G的估计

基于线性拟合的回归残差，利用改进的神经网络BP算法求解参数G。具体过程为

(1)计算n期变形观测数据的回归残差vi

(2)利用n期变形观测数据的所有信息构成神经网络模型:①选定输入层:由变形观测值产生影响的因素，设为(X1(i)，X2(i)，…Xt(i))和回归残差 vi组合构成;②选定输出层:参数G;③ 构造迭代模型:在对BP算法进行深入研究的基础上，提出了误差分级迭代的改进BP算法，它能有效地提高BP网络的稳定性。其基本思路为:先将设定的学习误差ε0进行分级，若将ε0分为n级，则分级公式为:

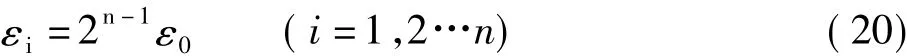
然后依次取εi为收敛控制参数对学习样本集进行学习训练，当第n级误差ε0迭代收敛后，网络的学习过程结束［6］。

4 工程实例

以某混凝土大坝5#104点2003年1月～2006年12月的垂直位移作为实验数据，根据原始的观测资料的水位和温度数据，共选出48组子样，其中2003年1月～2005年12月的共36组样本用来建模，2006年1月～2006年12月的共12组进行预测。为了分析出该大坝的形变规律，分别建立多项式回归分析模型、基于时间序列的半参数回归模型和基于线性回归的神经网络精化模型，用3个模型进行预报，对预报的结果进行比较。

4.1 回归模型

回归模型采用二次多项式模型，其中，xi表示坝前水位，yi表示温度，利用最小二乘法求解出回归方程:

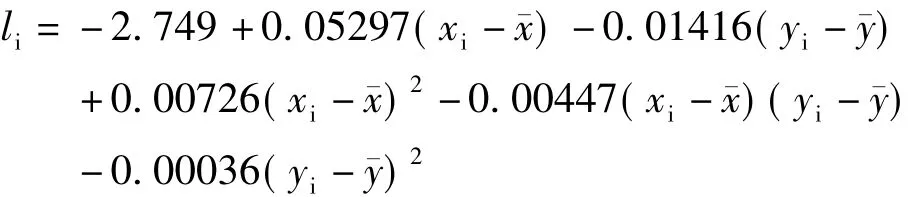
通过计算得二次多项式模型的内符合精度为±0.322 mm，外符合精度为±0.305 mm。

4.2 基于时间序列的半参数回归分析模型

建立半参数模型的关键是构造平滑参数和正规化矩阵。平滑参数利用交叉核实法确定为α=0.21，因为变形分析的观测数据具有时序性，所以选取基于时间序列的正规化矩阵，建立时间序列半参数回归分析模型。

为了分析平滑参数的选取对半参数拟合结果的影响，选取不同参数进行实验计算，计算结果如表1所示。

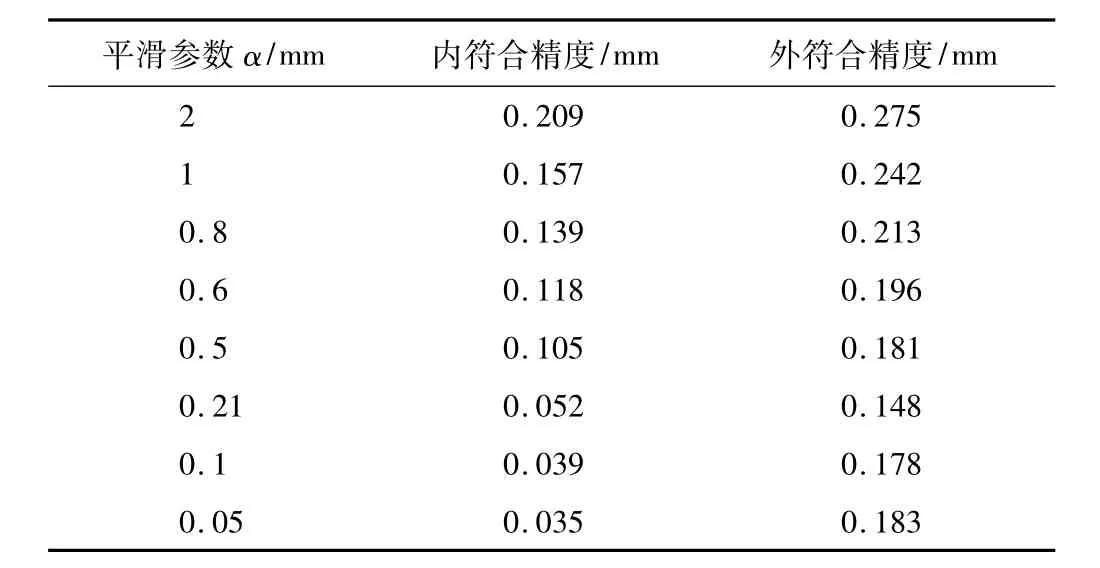
不同平滑参数实验结果比较表1

分析结果我们可以看出，对于该工程实例，随着平滑参数逐渐变小，内符合精度不断提高，说明该模型的学习能力在不断提高。同时，根据交叉核实法计算的平滑参数为0.21，外符合精度达到0.148 mm，说明平滑参数的选取基本符合实验要求，利用交叉核实法确定平滑参数就有一定的可靠性。

4.3 基于线性回归的神经网络精化法

采用二次多项式模型为基础模型，计算二次多项式的回归残差。以影响大坝垂直位移的温度、水位以及回归残差vi作为输入层，设精化值为输出层，建立基于线性拟合残差的神经网络模型。为了分析神经元数目对模型精度的影响，选取不同的神经元数目进行实验，计算结果如表2所示。

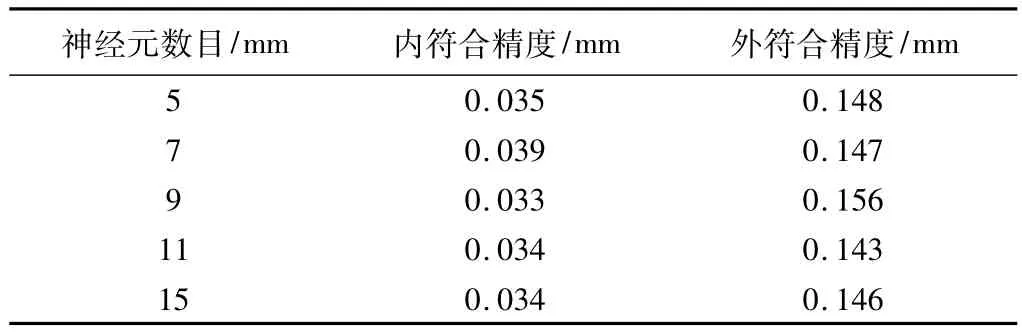
不同神经元实验结果比较表2

通过对不同的神经元数目进行实验分析，我们发现，外符合精度和内符合精度基本保持不变。对于该工程实例，模型具有较高的稳定性。

4.4 不同模型比较

通过以上3个模型的实验计算，我们选取平滑因子0.21的半参数模型，神经元数目11的神经网络精化模型以及二次多项式模型与实测值进行比较分析，数据结果如表3所示。

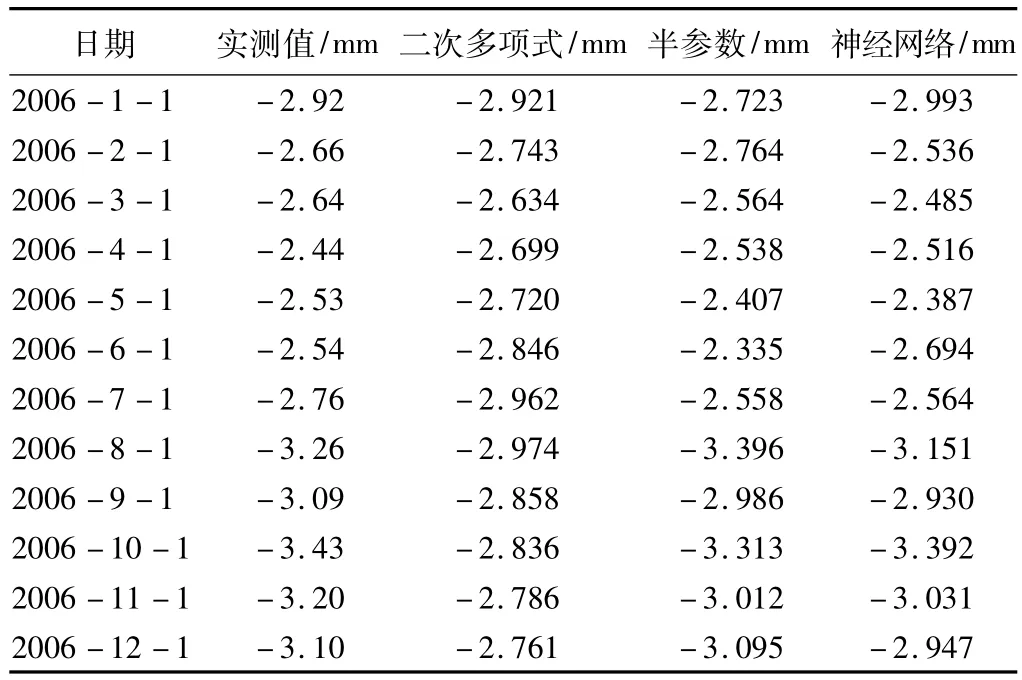
不同模型实验结果比较表3

通过实验，我们可以得到二次多项式的内、外符合精度分别为 ±0.322 mm和 ±0.305 mm，时间序列半参数模型的内、外符合精度分别为 ±0.052 mm和±0.148 mm，基于线性回归的神经网络模型的内、外符合精度分别为 ±0.034 mm和 ±0.143 mm。比较发现，相对于简单的二次多项式模型，后两种混合体模型无论是在内符合精度，还是在外符合精度上都有很大的提高。而两种混合体模型相比，神经网络模型的内符合精度更高，说明其学习能力更强，而在外符合精度上。两个模型基本相同，说明两者的预测能力基本相当，都具有很强的预测能力。