刘金堂，杨晓东，闻邦椿

(1.沈阳航空航天大学 航空宇航工程学院，沈阳 110136;2.东北大学 机械工程与自动化学院，沈阳 110004)

轴向运动薄板普遍存在，如动力传送带、磁带、带锯、印刷纸张、轧制中的板带钢等。运动薄板极易失稳，产生有害的横向振动:带锯的横向振动将影响切割质量并加剧锯的磨损;轧制中的板带钢的振动可引起板带钢扭曲甚至引起撕裂;动力传送带的振动引起带跑偏并影响设备寿命等。同时，轴向运动连续体作为典型陀螺连续系统，由于陀螺项的存在也对振动的分析和控制提出了若干重要的理论问题。

国内外众多学者对轴向匀速运动小挠度弯曲薄板的振动和稳定性进行了大量研究。Ulsoy等［1］研究了宽带锯片的振动特性;Lengoc等［2］分析了带锯锯片在切割工况时的动态响应;Lin［3］分析了轴向运动板的长宽比和刚度对稳定性的影响;Kim等［4］应用一种特殊单元法研究了受均布轴向拉力匀速运动薄板的振动特性;Hatami［5］研究了弹性支撑轴向运动板的振动和稳定特性;Yin［6］研究了轴向运动薄板横向非线性振动内部共振的基谐波响应;周银锋等［7］研究了轴向运动粘弹性板的横向振动特性。实际上，薄板并不是以严格的均匀速度运动的，由于各种因素的影响，速度通常具有周期脉动量，系统会表现出更加复杂的动态特性，且薄板在振动过程中，挠度有时不一定远小于厚度，这时，就必须考虑中面内各点的面内位移引起的几何非线性。

本文研究四边简支轴向变速运动大挠度薄板的非线性动力学行为。在von Kàrmàn大挠度板理论基础上，利用达朗贝尔原理得到轴向变速运动薄板的非线性运动微分方程，采用Galerkin方法对其离散，然后假设薄板运动速度具有周期脉动量，用数值方法分析所得常微分方程，研究薄板运动平均速度、速度脉动幅值和外激励力等参数对板非线性运动特性的影响。结果发现系统在上述参数变化时，均产生了分岔，经历了周期运动、倍周期运动、概周期运动，直至在平衡位置失去稳定性而出现混沌运动。

1 运动方程

考虑一四边简支匀质等厚矩形薄板，建立图1所示直角坐标系，xoy平面与薄板中面重合。薄板x和y向尺寸分别为a和b，薄板厚度为h，板沿x轴运动速度为V(t)，单位面积质量为ρ，材料的杨氏模量为E。F为x面单位长度上的拉力，q为薄板受到的垂直于板面的单位面积外激励力。板内任一点在x，y，z向的位移分别为 u(x，y，z，t)，v(x，y，z，t)，w(x，y，z，t)。

图1 轴向变速运动薄板Fig.1 Axially accelerating plates

在von Kàrmàn大挠度板理论基础上，应用达朗伯原理可得轴向变速运动大挠度薄板运动微分方程［8］:

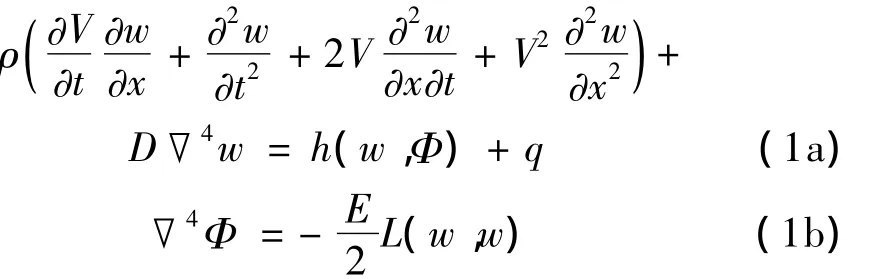
式中，D=Eh3/［12(1－μ2)］，μ为泊松比，Φ为应力函数，▽4为双调和算子，L(w，Φ)为非线性微分算子。

在x=0和a的两边上，有水平拉力F，在y=0和b的两边上，无边界力。故四边简支大挠度板的边界条件为:

式(2a)为位移边界条件，式(2b)为应力边界条件。引入如下无量纲变量及参数:

可得无量纲化运动微分方程:

边界条件式(2)则化为:

2 Galerkin截断

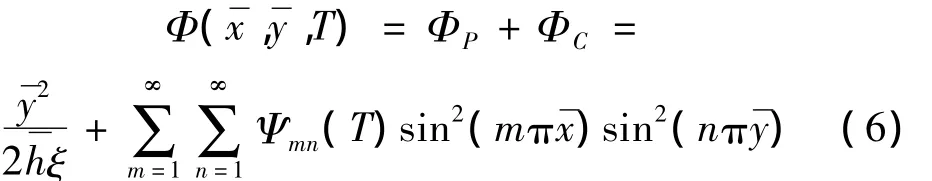
而挠度函数取为:

为方便讨论，四边简支条件下的公式推导和计算取 m=1，2，n=1，即:

将式(8)和式(9)代入式(4b)，并进行Galerkin积分:

得到:

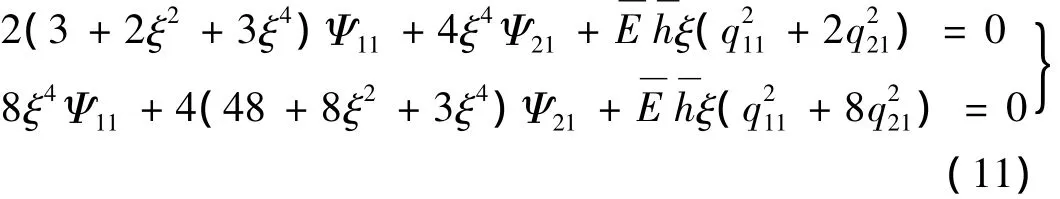
解式(11)得应力函数:

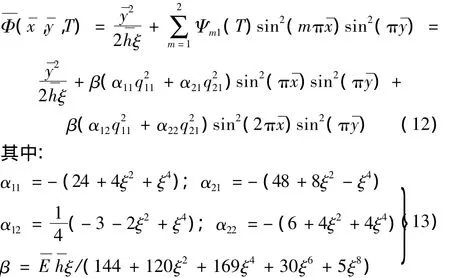
将应力函数表达式(12)和挠度函数表达式(9)代入式(4a)，并再次进行Galerkin积分:

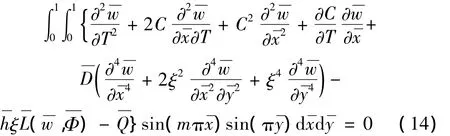
得到离散后的振动微分方程组:

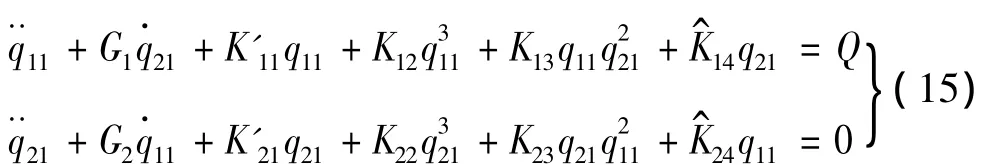
设薄板轴向运动速度带有周期脉动量:

其中，C1为速度脉动振幅(正实数小量)，C0为平均速度，Ω为速度脉动频率。将式(17)代入式(15)得:

其中:

考虑系统阻尼的影响并引入如下参数变量:

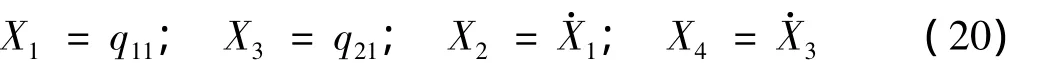
则式(18)变为:

式中的η1和η2为无量纲线性阻尼系数。

3 数值计算

通过分析式(21)，可以得到系统动力学特性随薄板运动平均速度C0，外激励力Q等参数的变化情况。薄板参数设定为:长度a=1 m，宽度b=1 m，厚度h=0.004 m，单位面积质量ρ=31.2 kg/m2，泊松比μ =0.3，杨氏模量E=2×1011N/m2，轴向拉力F=1 000 N/m。

用Poincaré映射图和最大Lyapunov指数分析系统动力学特性的变化。设定速度脉动频率为一固定值，绘出每一周期间隔处薄板中点处的位移和速度分岔图。

3.1 速度脉动幅值对非线性特性的影响

设定无量纲线性阻尼 η1=η2=0.7，外激励力Q=3 200，速度脉动频率 Ω=33，平均速度 C0=12，初始值为［1 ×10－6，0，1×10－6，0］。改变速度脉动幅值C1得到的分岔图和最大Lyapunov指数如图2所示。

图2显示，薄板以匀速运动时，系统为周期运动，当C1达到0.46时，产生Hopf分岔，由周期运动进入2倍周期运动，C1继续增加到1.82时，由倍周期转入概周期运动，随后当C1=1.835时，从概周期运动转为16倍周期运动，其间为倍周期与概周期运动的不断转换，最后，在C1=1.92处，LLE值开始大于零，由概周期运动通向混沌

图3、图4分别为C1=1.874时的概周期运动和C1=2时的混沌运动相平面图和Poincaré映射图。

图2 系统随C1的分岔及最大Lyapunov指数Fig.2 Bifurcation and the largest Lyapunov exponent versus the velocity amplitude

图3 概周期运动Fig.3 The quasi-periodic motion

3.2 平均速度对非线性特性的影响

图4 混沌运动Fig.4 The chaotic motion

设定无量纲线性阻尼η1=η2=0.7，外激励力Q=3 000，速度脉动频率 Ω =33，速度脉动幅值C1=0.7，初始值为［1×10－6，0，1 ×10－6，0］。改变板平均速度C0得到的分岔图和最大Lyapunov指数如图5所示。图6为薄板中点速度分岔图的局部放大图。

图5 系统随C0的分岔及最大Lyapunov指数.Fig.5 Bifurcation and the largest Lyapunov exponent versus the mean velocity

图5和图6显示，在C0=11.75处，系统产生 Hopf分岔，由周期运动转入2倍周期运动，当平均速度达到13.42时，进入概周期运动，在C0=13.48处，由概周期转入14倍周期运动，当平均速度达到13.485时，再次产生Hopf分岔，进入28倍周期运动，随后连续分岔，最后在C0=13.51处由倍周期分岔通向混沌，随着速度的持续增加，系统又经历了14倍周期，当C0=13.533时，LLE＞0，由爆炸性分岔通向混沌，于C0=13.588处，进入16倍周期，随后又经历了2倍周期运动，在C0=13.78处，又产生Hopf分岔，进入4倍周期运动，连续分岔，最后在C0=13.92处，由爆炸性分岔第三次通向混沌。图中共有三个区域出现混沌，但通向混沌的道路是不同的，一次是由倍周期分岔通向混沌，两次是由爆炸性分岔通向混沌。

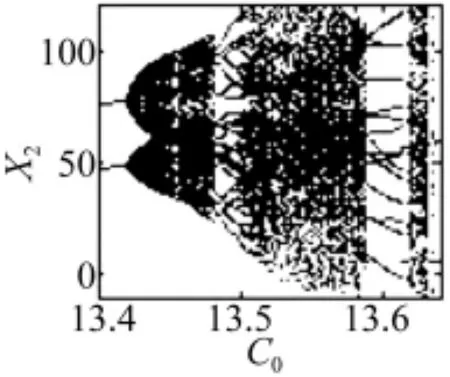
图6 X2随平均速度C0的分岔Fig.6 Bifurcation of X2 versus the mean velocity C0

图7和图8分别为C0=13.46时的概周期运动和C0=14时的混沌运动相平面图和Poincaré映射图。

图7 概周期运动Fig.7 The quasi-periodic motion

图8 混沌运动Fig.8 The chaotic motion

3.3 外激励力对非线性特性的影响

设定无量纲线性阻尼η1=η2=0.8，平均速度C0=14，速度脉动频率Ω=33，速度脉动幅值C1=0.6，初始值为［1×10－6，0，1×10－6，0］。改变外激励力 Q 得到的分岔图和最大Lyapunov指数如图9所示。

图9显示，系统产生了倒分岔，当Q的值在3 200处时，系统为2倍周期运动，随着Q的逐渐减小，在Q=3 158时产生分岔，进入4倍周期运动，随着Q值的继续减小，又连续产生Hopf分岔，最后在Q=3 049.7处，由倍周期分岔通向混沌。

图9 系统随Q的分岔及最大Lyapunov指数Fig.9 Bifurcation and the largest Lyapunov exponent versus the excitation amplitude

4 结论

本文研究了四边简支轴向变速运动大挠度薄板非线性横向振动的动力学特性。在von Kàrmàn大挠度板理论基础上，利用达朗贝尔原理推导轴向变速运动薄板的非线性横向振动微分方程组，采用Galerkin法将时间变量和空间变量、位移函数和应力函数分离，然后用数值方法分析所得常微分方程组。当板无量纲运动平均速度、外激励力和速度脉动幅值变化时，板中点处的位移和速度的分岔图中均出现了分岔，系统相继经历了周期运动、倍周期运动、概周期运动，甚至混沌运动。共发现了3条通向混沌的道路:由倍周期分岔、爆炸性分岔和概周期通向混沌。

［1］ Ulsoy A G，Mote J C D.Vibration of wide band saw blades［J］.J.Engng.Ind.，1982，104:71 －78.

［2］ Lengoc L，Mccallion H.Wide bandsaw blade under cutting conditions，part I:vibration of a plate moving in its plane while subjected to tangential edge loading［J］.J.Sound Vib.，1995，186(1):125－142.

［3］ Lin C C.Stability and vibration characteristics of axially moving plates［J］.Int.J.Solids Structures，1997，34(24):3179－3190.

［4］ Kim J， Cho J， Lee U，et al. Modal spectral element formulation for axially moving plates subjected to in-plane axial tension［J］.Comput.Struct.，2003，81:2011 － 2020.

［5］ Hatami S，Azhari M.Stability and vibration of elastically supported axially moving orthotropic plates［J］.Iranian Journal of Science＆ Technology，2006，30(B4):427－446.

［6］殷振坤，陈树辉.轴向运动薄板非线性振动及其稳定性研究［J］.动力学与控制学报，2007，5(4):314－319.

［7］周银锋，王忠民.轴向运动粘弹性板的横向振动特性［J］.应用数学和力学，2007，28(2):191－199.

［8］刘金堂.轴向变速运动机械薄板的非线性动力学特性［D］.沈阳:东北大学出版社，2010.