张万里，王常虹，夏红伟，解伟男

(1.哈尔滨工业大学空间控制与惯性技术研究中心，150001哈尔滨，zhangwanli1983@gmail.com;2.中国空空导弹研究院，471009河南 洛阳)

近年来交会对接技术一直是研究的重点之一[1]，而空间交会的制导律设计是完成交会任务的关键，目前近距离交会制导律的设计一般为脉冲推力的假设情况下的多脉冲机动，如Hari B.H[2]提出的使航天器相对速度随着距离指数下降，从而保证交会安全的制导方法，Lopez[3]提出势函数制导法，将目标点处势能设置为最小，而初始位置和障碍处的势能设置为较大值，通过使航天器沿着势能减小方向运动从而使其向目标靠近并实现避障机动.梁立波[4]提出的斜滑制导算法，采用对数函数映射法进行脉冲寻优，实现燃料最省交会.但因实际交会时脉冲推力假设一般无法满足，航天器的速度改变需要一定的时间，此时必然存在推力弧段与自由飞行弧段，当考虑此因素后实际交会轨迹与名义轨迹偏差较大，针对如何对实际轨迹进行闭环校正使其终止位置与名义轨迹重合，陈伟跃[5]设计了小推力速度闭环交会制导律，通过对若干制导周期内的速度脉冲求取实现轨迹校正，但其实现需要若干不定的制导周期，且在每个周期内需重新求取速度脉冲，计算量复杂.

随着高比冲小推力推进系统的日益成熟，采用小推力推进器实现轨道交会可以避免脉冲假设带来的轨迹偏差，且通过设计轨道各个方向的控制变量变化，可以实现燃料最优交会.本文使用高比冲小推力推进系统为执行机构，设计空间交会问题的燃料最优时间连续制导律.首先给出轨道交会问题的数学模型，并给出最优控制问题的目标函数和约束条件，然后利用直接法将控制变量离散化，通过参数寻优得到对应燃料最优的控制变量参数和交会时间常数，从而求得最优交会轨迹.

微分代数(differential algebraic，DA)是由Martin Berz[6]建立的利用代数方法求解解析问题的有效手段.P.D.Lizia[7]将此应用在对星际间连续小推力的轨道转移的修正上，R.Armellin[8]将其用于行星引力辅助轨道转移问题.本文将该方法应用于轨道交会情形.因在轨道交会推进系统的实际点火时刻与名义点火时刻常常存在一定量的偏差，从而导致实际交会轨迹与名义交会轨迹同样会存在偏差.本文针对此情况，首先给出利用微分代数方法实现常微分方程积分的途径，并对初值扰动情形下，微分代数变量阶数不同对于积分轨迹的影响情况进行分析，最后利用微分代数工具求取小推力情况下点火时刻偏差对应的部分控制变量修正值，从而完成轨迹修正.

1 求解航天器交会燃料最优控制问题

1.1 航天器交会相对动力学方程

在交会的最终逼近阶段，可以由Clohessy-Wiltshire(C-W)方程来近似描述2个飞行器的相对运动状态.该方程建立在目标航天器的当地垂直当地水平(local-vertical-local-horizontal，LVLH)坐标系下，坐标系各轴具体方向如图1所示.

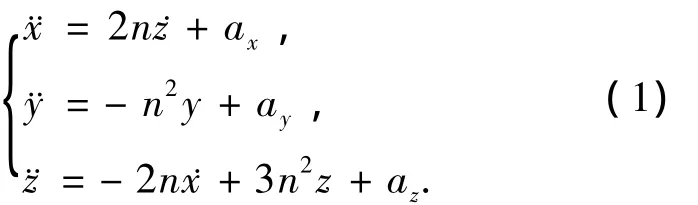
在LVLH坐标系下得到的线性化后简化C-W方程，具体形式为其中:ax、ay、az表示在LVLH坐标系中施加于追踪航天器上的3个方向的加速度，n为目标航天器的轨道角速度.本文通过对控制变量ax、ay、az的设计，使航天器轨道交会过程燃料实现最优，并求出对应的最优轨迹.

图1 当地垂直当地水平坐标系

1.2 利用直接法求解燃料最优交会问题

对于航天器在连续推力下的燃料最优轨迹优化问题，目前常用的数值方法包括间接法和直接法.间接法通过对原始问题的一阶最优必要条件进行离散化，求解满足此条件的方程，从而得到满足原始最优控制问题的解.但此法求解繁琐，收敛域小，对于各种变量尤其是无实际物理意义的协态变量初值猜测难度高.直接法通过将控制变量离散化，避开最优必要条件的求解步骤，通过将离散节点处的控制变量值设置为寻优参数，后利用寻优函数求取此最优控制问题.直接法相比而言具有收敛域大、求解简单、无需对协态变量进行初值猜测等优点，因此其实用性较强，也是当前求解此类问题的主流方法.本文利用直接法求取燃料最优的最优控制问题，下面具体说明其在轨道交会问题上的实现方式.

1)确定交会过程中间停靠点.基于文献[2]中提出的使航天器相对速度随着距离指数下降的制导方法，本文按照以下方式确定交会过程中保持点的位置和速度:假设初始交会位置与目标位置距离为r0，则若干个位置保持点与目标位置成比例k1下降，即越靠近目标，转移轨迹范围越小，同时使速度幅值成比例k2下降，保证航天器交会过程中速度越来越小.在将交会过程分段完毕后，对每段独立求解燃料最优问题，同时每段的初始时刻的位置、速度和终止时刻的位置、速度已给定.

2)离散化控制变量.首先要进行离散化控制变量，通过将每一阶段轨道交会时间三等分得到包括初始时刻和终端时刻在内的4个时间节点，分别设置为 T0、T1、T2、T3.将每个时间节点处的控制变量设置为寻优参数 Ux0、Uy0、Uz0、…、Ux3、Uy3、Uz3，因轨道交会涉及 x、y、z 3 个方向，因此得到12个控制变量参数.同时因轨道交会时间未定，将轨道交会所需时间Ttrans设置为独立参数，共记13个参数.

3)建立必要的约束条件.由于每个阶段轨道交会的终止位置和速度都已给定，对于终端位置和速度存在共6个约束条件，即

式(2)中的航天器终端状态 RT、VT通过对C-W方程进行积分求得，积分中的连续变量ax、ay、az通过对控制变量参数 Ux0、Uy0、Uz0、…、Ux3、Uy3、Uz3进行Lagrange插值获得，交会时间Ttrans同样为待优化参数.

4)确定所需目标函数.本文需要求取燃料最省轨道交会问题，因此其目标函数可设置为

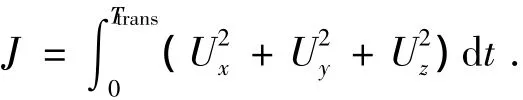
其中Ux、Uy、Uz同样通过对控制变量参数进行Lagrange插值获得.

5)参数寻优.通过以上步骤定义了轨道交会燃料最少最优控制问题所需的离散化寻优参数，各种约束条件以及最优控制的目标函数，利用Fmincon函数即可完成寻优过程.通过对12个控制变量参数进行Lagrange插值即可得到在各个阶段轨道交会问题所需的连续控制变量ax、ay、az.

2 利用DA求解存在点火误差时控制变量修正值

上节利用直接法求出了燃料最省的名义最优交会轨迹，但在实际完成轨道转移的过程中，航天器的初始状态常常存在扰动情况，本文就以实际点火时刻与给定时刻存在偏差为例，利用微分代数方法求解关于部分控制变量的修正问题.首先对于利用DA工具实现常微分方程积分的途径进行简要说明，并给出其针对初值扰动进行灵敏度分析的办法.然后针对点火时刻偏差情形，利用微分代数工具给出求解控制变量修正值的具体步骤.

2.1 利用微分代数工具积分常微分方程

微分代数是由Martin Berz在上世纪八十年代末发展起来的利用代数方法求解解析问题的一种有效的手段，利用微分代数工具，可以求取多元函数关于变量的任意阶泰勒展开，并根据对其泰勒展开系数的各种操作，实现对原函数的复合运算、求逆运算、积分常微分方程、求解两点边值问题(two point boundary value problem，TPBVP)、进行参数灵敏度分析等.本文利用COSY Infinity软件实现以上操作，其中包含了DA数据类型的定义及一些基本的函数操作方法，可以方便的利用微分代数解决实际问题.因求解轨道交会问题需进行积分操作，下面针对DA实现常微分方程积分以及对初值扰动的灵敏度分析，简单介绍DA的使用方法.

利用计算机实现任何数值积分操作，都是通过求取在若干积分点处的函数值后对其进行代数操作完成的，以一维初值问题为例:

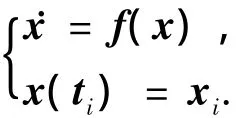
考察对式(2)实现的第一步欧拉前向积分，即

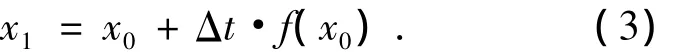
对于目前常规的数值积分程序，将其中x0=xi取为变量初值时，即可求取经过Δt时间间隔后的变量取值x1.但在微分代数框架内实现此过程，需将初值xi设置为变量初值与DA变量da相加的形式，即

通过将此数值积分过程在DA框架内继续，即可得出在积分结束时刻tf处变量x关于初值的taylor展开值.即

利用式(4)，选择不同的初始值扰动daxi，即可通过简单的多项式代入操作求取积分终止时刻变量xtf的取值，而不必对每一个实际初始值重新进行数值积分操作，因此可非常方便的实现对于初值的灵敏度分析操作.而当DA变量选取的阶数不同时，利用DA工具求取的xtf的准确性也有所不同，这将在后面的仿真分析中具体说明.

2.2 存在点火时刻偏差时利用DA求解制导律的修正值

利用微分代数方法，可方便的在存在点火时刻误差情况下，求取相应的节点处控制变量的修正情况，而不必针对每种实际情况重新求解最优控制问题，具体求解步骤如下.

1)首先定义一点火时刻滞后偏差DA变量da(1)，从而求得航天器轨道交会所需时间为

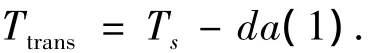
其中Ts分别是上节求出的名义轨道交会时间.在实际点火时刻之前，航天器在无推力情形下，即式(1)中 ax、ay、az=0 条件下运动，运动时间为da(1).

2)针对上述最优控制问题离散化的4个节点以及12个控制变量而言，本文假定存在点火时刻偏差情况下，对于初始时刻节点和终止时刻节点处的控制变量进行修正，因此可定义6个DA变量da(2)～da(7)，分别对应T0和T3时刻3个方向的控制变量修正值.

3)首先通过对动力学方程(1)在ax、ay、az=0条件下积分da(1)时间，从而求取实际的初始点火时刻时航天器对应的位置和速度值.然后，对动力学方程(1)积分Ttrans时间，求取终端位置和速度值.由于此时积分时间da(1)和Ttrans中包含待定DA变量，可将原始动力学方程转化为

这样只需进行[0，1]时间间隔内的积分操作，即可完成方程ODE积分过程，从而避免了在积分时间内存在DA变量的问题.

4)此时对常微分方程积分可求得对应于终止时刻的位置和速度关于初始位置和初始速度的函数关系式，通过简单的多项式代入即可求得

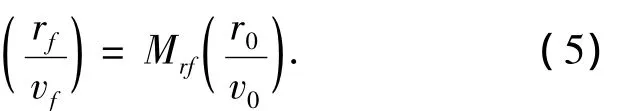
而此时的r0、v0都只与点火时刻Tini有关.

将式(5)两边的名义初始位置、初始速度和终止位置、终止速度减去，则可得如下的对应于位置速度偏差的关系式:

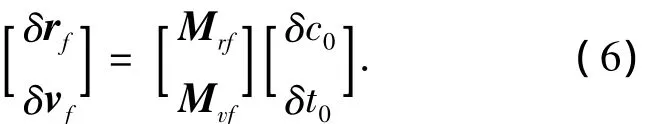
其中 δc0为 6维控制变量修正向量，因此[δc0δt0]T为7维向量.为使得关于DA的求逆运算成为可能，在方程(6)的左边增广一行δt0，得到如下关系式:

妹妹将父母在小城最后一套房子卖掉——这次回去，基本上算无家可归了，暂借于妹妹同学家。小区临江，大约是过去三号码头的位置。无论清晨，抑或日暮，站在阳台，可闻江水气息。

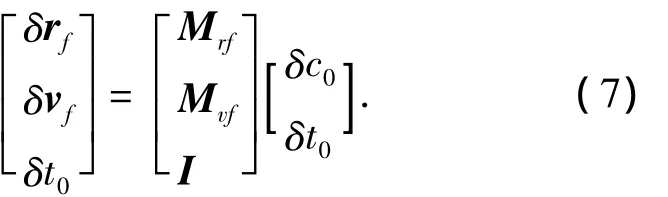
5)式(7)中[MrfMvfI]T为7维方阵，进行求逆运算，利用COSY软件中关于DA变量的求逆算子MI，即可完成求逆操作，如下:

因为对于轨道交会问题，要求终止时刻的航天器位置向量和速度向量与名义位置向量和名义速度向量相同，因此可将上式中的δrf和δvf设置为零.即可求得针对于点火时刻偏差δt0所需的控制变量校正值δc0，将此校正值与名义控制变量相加，即可得到时间节点T0和T3时刻的新的控制变量值.

3 仿真分析

针对上节内容进行仿真验证，首先给出利用直接法求取的航天器交会燃料最优轨迹以及航天器速度、质量和控制变量随时间的变化关系.然后给出利用微分代数方法实现常微分方程积分的具体仿真结果.当初值存在一定量扰动，且选取DA变量阶数不同时，给出利用DA工具所得的初值扰动灵敏度分析结果与真实数值积分结果的关系.最后给出在初始点火时刻与名义点火时刻存在偏差情形下，利用微分代数方法求取的控制变量修正值以及航天器的修正轨迹.

3.1 直接法求取的最优轨迹

按照1.2节方法，利用直接法通过对其寻优得到在满足各种约束条件情况下，目标函数最小的14个参数变量，将参数变量中的控制变量关于时间进行Lagrange插值，即可求得所需的控制推力函数.仿真中所选目标航天器初始轨道参数如表1所示.

表1 航天器初始轨道参数

追踪航天器质量为1 000 kg，小推力发动机比冲为3 000 s.按照1.2节求取中间位置保持点，取k1=5，k2=10.即位置以5倍减少速度向交会点靠近，速度以10倍减少速度降低.可得到追踪飞行器在目标飞行器LVLH坐标系中的初始位置、速度和保持点位置、速度如表2所示.

表2 航天器位置速度参数

图2～图5分别给出了求解的追踪航天器的x、z向位置名义最优轨迹，速度、控制变量和质量随时间的变化关系.利用直接法求取的每个阶段的交会时间分别为 146.42、191.86和 157.58 s，图2中小图分别给出了追踪航天器在交会保持点的轨迹细节图，从图中可见，追踪航天器可以在交会保持点满足指定位置和速度要求.推进发动机各个方向的推力随时间由大变小，至1E－4数量级.航天器质量从初始的1 000 kg减少至973.4 kg，共消耗燃料26.6 kg.

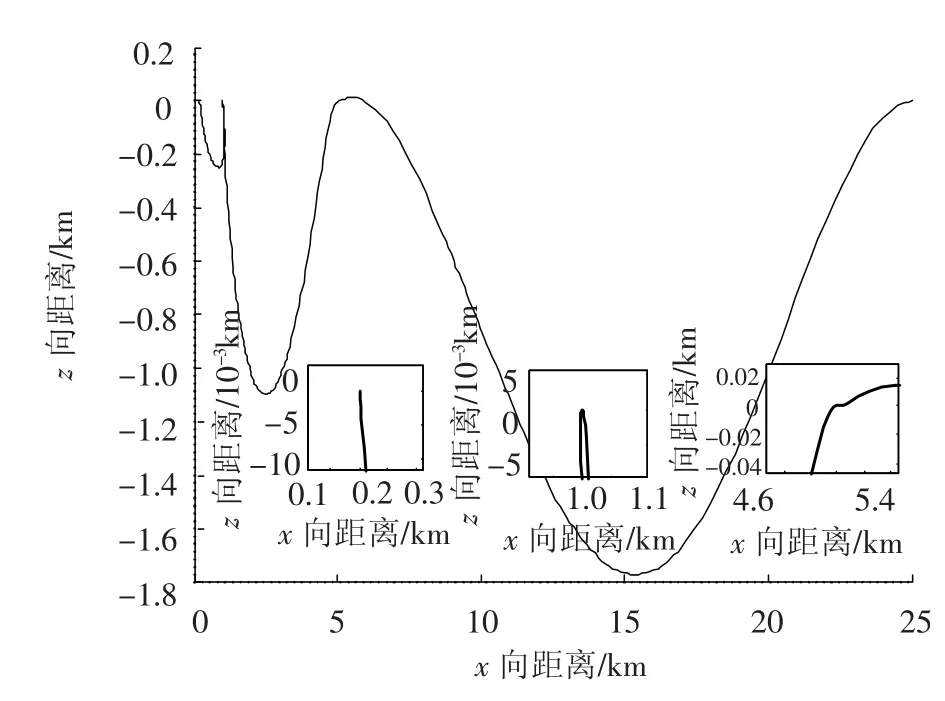
图2 轨道交会的名义轨迹

图3 名义速度随时间的变化关系

图4 名义控制变量随时间的变化关系

图5 航天器质量随时间的变化关系

3.2 利用DA工具实现常微分方程积分仿真

本节以近地航天器围绕地球的运动轨道为例，利用DA工具实现积分操作，航天器动力学方程为

航天器的初始轨道参数如表1所示，首先由初始轨道参数求出航天器的初始位置和速度，然后积分ODE方程得出航天器的运行轨迹，积分时间取一个周期T=6 556 s.为了说明利用DA工具对初值扰动进行灵敏度分析的效果，同时给出当x、y方向初始位置存在300 km偏差时的积分轨迹变化情况.

图6和图7分别给出了是否存在初值偏差时，利用DA工具所得到的积分曲线与直接利用ODE45进行积分的结果比较图，从图中可以看到，当不存在初值偏差时，曲线对于DA变量的阶数并不敏感，而当x、y方向分别存在初值偏差为300 km时，随着DA变量阶数的增高(vorder=1、3、5时)，利用DA方法所得到的结果与针对不同初值重新进行ODE积分所得到的积分结果基本一致.但利用微分代数方法求解初始偏差对积分路径的影响，只是采用了简单的多项式代数操作，与重新对原始ODE方程进行积分运算相比运算量大大减少.

图6 航天器运行轨迹3维示意

从图8中不同阶数下x方向的误差得出，随着时间的增加，积分误差逐渐增大，但当vorder=5时，一个周期内的积分误差可以保持在很小的范围内.

图7 航天器运行轨迹2维示意

图8 x方向误差对比

为详细说明DA实现ODE方程的情况，下面给出当选取三阶DA变量时，x方向上的Taylor展开系数如表3所示.

表3 x方向Taylor展开系数

由以上数据可知，5 224.003 981 650 331为不存在初值扰动时刻的航天器终止位置，经计算比较可见，经过1个周期后，航天器可返回原始位置，而当存在初值偏差时，对于终止位置的影响可以通过直接将偏差值代入Taylor展开式获得，从而避免对应于每个不同的偏差值重新进行积分操作，可节省大量的计算量.当vorder越大，对于初值偏差的灵敏度分析越准确.为使结果精确，本文仿真中微分代数变量阶数取为5.

3.3 存在点火时刻偏差时的航天器交会轨迹修正

由于各种原因致使航天器初始点火时刻与所求取的名义点火时刻可能存在一定的偏差，从而导致此时的轨道交会轨迹与名义轨迹偏差较大，无法完成给定交会任务.本文假定航天器在3个交会阶段的点火时刻分别延后3 s、10 s、10 s情况下，首先给出此时实际位置轨迹与名义最优轨迹的对比.

从图9中可以看出，随着每个交会阶段的误差累计，最终的 x、z方向偏差分别在400 m和250 m左右，无法满足交会要求，需要进行轨迹修正.下面给出利用微分代数方法求解的控制变量修正曲线以及修正后的交会轨迹.

图9 轨道交会的轨迹对比

图10为控制变量随时间的变化，由图中可以看出，修正后的控制变量轨迹与前者相差不大，一般在1E－5数量级，因此所消耗燃料情况与名义轨迹对应燃料消耗变化不大.通过对修正前后轨道交会的轨迹对比(如图11所示)可知，航天器在位置保持点处的校正轨迹与名义轨迹基本一致，可以很好的解决由初始点火偏差导致的轨迹偏离问题，完成交会指标要求.

图10 控制变量随时间的变化关系

图11 修正前后轨道交会的轨迹对比

4 结论

本文针对实际航天器轨道交会中脉冲推力假设失效情况，利用小推力推进系统实现航天器的燃料最少交会制导律设计.

1)首先利用直接法将控制变量离散，给出最优控制问题对应的状态方程，约束条件和指标函数，并利用寻优函数得出最优控制变量和交会时间.从仿真结果可以看出，名义最优轨迹的位置和速度值基本满足交会要求，航天器消耗燃料为26.6 kg.

2)其次本文给出了应用DA工具实现积分的具体方法，仿真结果显示当存在初值扰动时，采用5阶DA变量即可使得积分曲线与实际ODE45积分曲线基本一致.

3)最后针对轨道交会中的点火时刻误差导致实际轨迹与名义轨迹有较大偏差的情况，利用微分代数方法，求取部分时间节点处控制变量的修正值，从修正后的轨迹可见，追踪航天器在各个位置保持点的位置与名义轨迹相应位置基本重合，因此此法可以较好的实现轨迹修正，且应用DA求取控制变量的修正值，无需重新求解轨迹优化问题，只需简单的多项式代数操作即可实现，从而节省大量的计算量，使得制导律的实现更为简单易行.

[1]刘暾，赵钧.空间飞行器动力学[M].哈尔滨:哈尔滨工业大学出版社，2003:83－101.

[2]HARI B H，MYRON T，DAVID D B.Guidance algorithms for autonomous rendezvous of spacecraft with a target vehicle in circular orbit[C]//AIAA Guidance，Navigation，and Control Conference and Exhibit 6 － 9.Montreal，Canada:AIAA，2001:1 －15.

[3]LOPEZ I，MCINNES C R.Autonomous rendezvous using artificial potential function guidance[J].Journal of Guidance，Control，and Dynamics，1995，18(2):237 －241.

[4]梁立波，罗亚中，唐国金.航天器近距离交会斜滑制导算法[J].国防科技大学学报，2009，31(5):125 －129.

[5]陈伟跃，荆武兴，程博.小推力速度闭环交会制导律设计[J].宇航学报，2009，30(3):1030 －1038.

[6]BERZ M.Handbook of accelerator physics and engineering[M].New York:World Scientific，1999:81 －117.

[7]LIZIA P D，ARMELLIN R，ERCOLI-FINZI A.Highorder robust guidance of interplanetary trajectories based on differential algebra[J].Journal of aerospace engineering，sciences and applications，2008，1(1):43 －57.

[8]ARMELLIN R，LIZIA P D.Gravity assist space pruning based on differential algebra[J].Celestial mechanics and dynamical astronomy，2010，106(1):1 －24.