曲元海

(通化师范学院 数学系，吉林 通化 134002)

1 引言

解 显然本题罗必达法则失效.故另谋方法.仔细观察该题后，我们发现由于被积函数含有|cost|项(本题关键就在于此)，而该函数是周期为π的非负函数.另一方面，当连续变量x充分大时，总存在n∈，使x可表成x=nπ+x0，其中0≤x0<π，故有x→+∞⟺n→∞.

此时，本题可转化为计算极限

由于

(1)

采用分部积分法，经计算获得

……………………………………

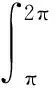
而对最后一项：

(1)当0≤x0<π/2时，令t=nπ+x，则有

(2)当π/2≤x0<π时，令t=nπ+x，则有

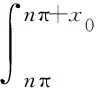
这时，将上述所有结果带回(1)式，我们得到分子部分

故得

另解 由于被积函数含有|cost|是周期为π的非负函数.故当x充分大时，总存在自然数n∈，使nπ≤x≤(n+1)π.因此，由积分的单调性得

(2)

依照前边定积分的计算方法得

(这里，对第二个积分取变量替换t=nπ+x).因此，当n→∞，必有

由(2)式及极限的两边夹定理，我们立即获得相同结果.

注意：上述两方法都离不开计算定积分，因此，两方法本质上有密切联系，只是求解角度不同.

3 推广

以下我们只考虑应用夹逼定理来求解.由于当k≥4时，不仅导致计算积分值繁琐，而且涉及高次幂的自然数求和.因此，本文我们仅限k=1，2，3时，推广如下两种对偶型积分的极限.

计算两种特定的对偶型极限：

k=1，2，3.

事实上，当x充分大时，总存在自然数n∈，使nπ≤x≤(n+1)π，再由积分的单调性得

(3)

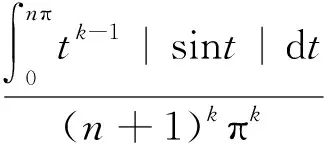
(4)

以下求解过程中，我们总是假设x→+∞时，存在n∈，使nπ≤x≤(n+1)π，不再特殊说明.

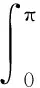
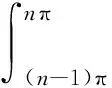
令k=1，代入(3)式，应用夹逼定理，立即获得

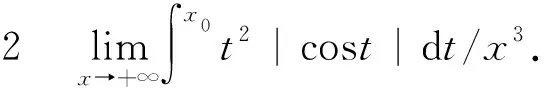
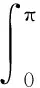
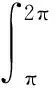
故

令k=3，代入(3)式，由夹逼定理，立刻获得

解 类似例1计算方法，更容易计算

令k=1，由(4)式及夹逼定理，显然获得

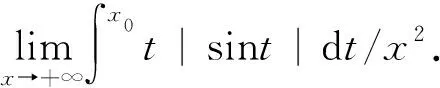
解 利用不定积分

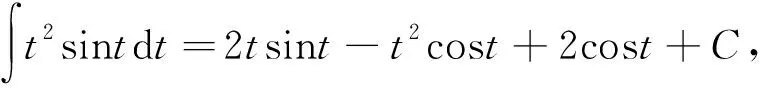
故

因此，必有

令k=3，代入(4)式，应用夹逼定理，我们获得

综上所述，获得本文如下的推广结论

最后，我们给出一个猜想，∀k∈，是否

参考文献：

[1]刘玉琏，傅沛仁.数学分析讲义[M].第三版.北京:高教出版社，1997.

[2]陈纪修，於崇华，金路.数学分析[M].北京;高等教育出版社，1999.

[3]刘三阳，于力，李广民.数学分析选讲[M].北京;科学出版社，2007.