余 静

（合肥师范学院 数学系，安徽 合肥 230061）

关于内接单形几个几何不等式及应用

余 静

（合肥师范学院 数学系，安徽 合肥 230061）

应用几何不等式理论与解析方法，研究欧氏空间En中n维单形的几何不等式问题，建立了关于单形与其内接单形的两个不等式，推广了已有的结果，推广了著名的n维Euler不等式。

欧氏空间；单形；内接单形；不等式

1 引言及主要结果

关于欧氏空间En中n维单形几何不等式的研究，近期获得很多重要的几何不等式，专著［1，2，3］收入了大量有关几何不等式。最近文献［4，5］中给出单形的内接单形之概念，并建立了关于单形的内切球半径与单形的内接单形外接球半径之间的两个重要不等式，它们推广了著名的n维Euler不等式［6］。本文研究了单形类似的几何不等式问题，建立相关几个不等式，它们推广了文献［4，5］中的主要结果，并应用它们推广了n维Euler不等式。

本文中约定En中n维单形σn的顶点集为｛A0，A1，…，An｝，顶点Ai所对侧面fi＝A0…Ai－1Ai＋1…An（n－1维子单形）的面积为Fi，σn的各棱长为aij＝｜AiAj｜（i，j＝0，1，…，n），σn的体积为V，外接球半径为R，内接球半径为r，σn的重心、外心、内心分别为G、O、I。

在n维单形σn的第i个侧面fi上任取一点A′i（i＝0，1，…，n），那么以A′0，A′1，…，A′n为顶点集的n维单形σ′n称为单形σn的一个内接单形［4］，设内接单形σ′n的外接球半径为R′，σ′n的棱长为a′ij＝｜A′iA′j｜（i，j＝0，1，…，n）。最近文献［4］获得单形与其内接单形的一个重要不等式：

当σn为正则单形且σ′n为其切点单形时等号成立。

特别，如果在不等式（1）中取σ′n为单形σn的切点单形，此时R′＝r，从（1）便得著名的n维Euler不等式［6，7］：

当σn为正则单形时等号成立。

最近，文献［5］获得关于内接单形另外两个不等式：

当σn为正则单形且σ′n为其切点单形时等号成立。

如果在不等式（4）中取σ′n为σn的切点单形时，即得n维Euler不等式（2）的如下推广［8］：

当σn为正则单形时等号成立。

一点注记：文献［5］中对不等式（3）的证明过程中有误，实际上不等式（3）并不成立，具体证明过程的错误可见文献［5］。

本文研究n维单形与其内接单形外接球半径与内切球半径不等式问题，建立有关一些不等式，由此推广了n维Euler不等式。本文主要结果是下面两个定理。

当σn为正则单形且σ′n为其切点单形时等号成立。定理1．2 对n维单形σn与其内接单形σ′n，有

当σn为正则单形且σ′n为其切点单形时等号成立。

由定理1．1与定理1．2可得：

推论1．1 对n维单形σn与其内接单形σ′n，有

当σn为正则单形且σ′n为其切点单形时等号成立。

如果在推论1．1中取σ′n为σn的切点单形，此时R′＝r，于是得到n维Euler不等式（1．2）的如下两个推广：

推论1．2 对n维单形σn，有

当σn为正则单形时等号成立。

由定理1．1、定理1．2，还可得如下两个推论：

推论1．3 对n维单形σn与其内接单形σ′n，有

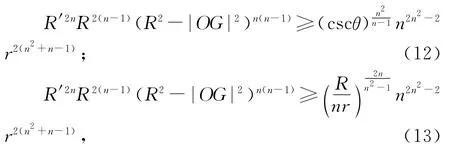
当σn为正则单形且σ′n为其切点单形时等号成立。

推论1．4 对n维单形σn与其内接单形σ′n，有

当σn为正则单形且σ′n为其切点单形时等号成立。

2 引理与定理的证明

引理2．1［9］对n维单形σn，有

等号成立当且仅当σn为正则单形。

引理2．2［10］对n维单形σn，有

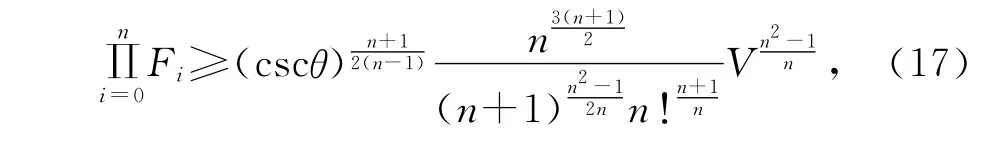
当σn为正则单形时等号成立。

引理2．3 对n维单形σn，有

当σn为正则单形时等号成立。

证：利用［11］中不等式：

当σn为正则单形时等号成立。

利用文献［13］中不等式

当σn为正则单形时等号成立。

引理2．4［2］对n维单形σn，有

引理2．5［4］对n 维单形σn与其内接单形σ′n，有

当σn为正则单形且σ′n为其切点单形时等号成立。

引理2．6［8］对n维单形σn，有

当σn为正则单形时等号成立。

证：引用［14］中一个不等式：

当σn为正则单形时等号成立。

由不等式（25）与（20）便得不等式（24）。

定理1．1的证明：由引理2．6，有

由（22）、（25），得

由（21）、（27）以及算术－几何平均不等式，得

利用［12］中不等式

当σn为正则单形时等号成立。由（28）、（29）及引理2．6，有

由（30）、（16）、（17），得

应用［4］中不等式

当σn为正则单形时等号成立。

由（31）、（32），得

即

所以不等式（6）成立，易知当σn为正则单形且σ′n为其切点单形时（6）中等号成立。

定理1．2的证明是类似的，只要应用不等式（30）、（18）、（24）及（32）便可得到不等式（7）。

［1］ Mitrinovic D．，Pecaric J．，Volence V．Recent Advances in Geometric Inequalities［M］．Dordrecht，Kluwer Acad．Publ．，1989．

［2］ 沈文选．单形论导引［M］．长沙：湖南师范大学出版社，2000．

［3］ 单墫，等．几何不等式在中国［M］．南京，江苏教育出版社，1996．

［4］ 杨世国．关于内接单形的一个几何不等式［J］．数学杂志，2003，23（2）：218-220．

［5］ 杨世国，陈士龙．关于内接单形的两个不等式及应用［J］．哈尔滨工业大学学报，2009，41（1）：229-231．

［6］ Klamkin，M．S．Inequality for a simplex［J］．SIAM Rev，1985，27：576-577．

［7］ Klamkin，M．S．The circumradius-inradius inequality for a simplex［J］．Math．Magazine，1979，52：20-22．

［8］ Yang S．，Wang J．Improvments of n-dimensional Euler inequality［J］．J．Geom．，1995，55（2）：190-195．

［9］ 冷岗松．Euler不等式的一个加强［J］．数学的实践与认识，1995，25（2）：94-96．

［10］ 杨世国．关于单形外接球半径的两个结果［J］．西安工程科技学院学报，2004，18（1）：91-94．

［11］ 苏化明．一个涉及单形体积棱长与侧面面积的不等式［J］．数学杂志，1993，13（4）：453-455．

［12］ 杨路，张景中．关于有限点集的一类几何不等式［J］．数学学报，1980，23（5）：740-749．

［14］ 匡继昌．常用不等式［M］．济南：山东科学技术出版社，2004．

［15］ 杨路，张景中．一个代数定理的几何证明［J］．中国科学技术大学学报，1981（4）：127-130．

Application and Generalization of some Geometric Inequalities for Inscribed Simplex

YU Jing（Department of Mathematics，Hefei Normal University，Hefei 230061，China）

In this paper，the theory of geometric inequalities and analytic method are emlployed to study the problems of geometric inequality for n-dimensional simplex in the Euclidean space En．Two geometric inequalities for a simplex and its inscribed simplex are established，some known results and the famous n-dimensional Euler inequality are improved．

Euclidean space；simplex；inscribed simplex；inequality

O 184

A

1674-2273（2011）06-0005-03

2011－06－10

安徽省高校省级重点科研项目（KJ2009A45）

余静（1971－ ），女，合肥师范学院数学系副教授，研究方向：距离几何、凸几何。