朱思念, 王 刚

(中国矿业大学 理学院, 江苏 徐州 221008)

半直线上一类分数阶耦合系统边值问题解的存在性

朱思念, 王 刚

(中国矿业大学 理学院, 江苏 徐州 221008)

讨论了一类半直线上分数阶耦合系统边值问题解的存在性,其中非线性项含有分数阶导数,通过建立合适的相对紧的判定准则,结合Schauder不动点定理,得到了解的存在性．

分数阶; 无穷区间; 不动点定理; 边值问题

0 引言

无穷区间上的边值问题起源于非线性椭圆方程对称解的研究,由于无穷区间不具有紧性,给讨论增加了一定难度,为此人们给出了一些判定相对紧的准则[1].近些年来,分数阶微分方程引起了人们的广泛兴趣,出现了许多出色的成果[2-5], 然而很少有文章讨论分数阶微分方程在无穷区间上解的存在性[6-8].在文[6]中,作者使用Schauder不动点定理结合对角化原理,讨论了如下无穷区间上有界解的存在性:

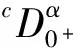
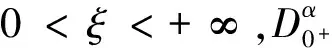
受上述文献启发,本文考虑如下分数阶无穷区间耦合边值问题

(1)

和

(2)

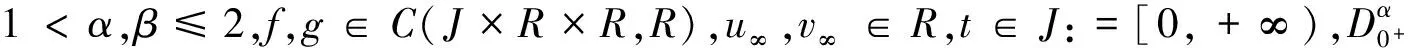
为方便起见,先给出一些预备知识和引理及假设.

1 预备知识和引理

定义1[5]函数y:(0,+∞)→R的α阶Riemann-Liouville分数阶积分为

其中αgt;0,Γ(·)为gamma函数.

定义2[5]连续函数y:(0,+∞)→R的α阶Riemann-Liouville分数阶导数为

其中αgt;0,Γ(·)为gamma函数,n=[α]+1.

其中N=[α]+1

本文总假设以下条件成立:

(H) 存在非负函数a(t),b(t),c(t),k(t),l(t),m(t)∈L1(J)使得

且满足

考虑空间

类似的有

由于无穷区间不具有紧性, 我们给出如下引理, 具体证明类似文献 [8] 的引理2.3.

引理2V⊆E为有界集, 即V={(x,y)∈E|‖(x,y)‖Elt;l}, 如果下列条件满足:

有

其中t1,t2≥T.

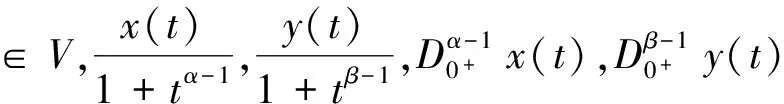
引理3 假设条件(H)满足, 则边值问题(1)(2)的解等价于以下积分方程

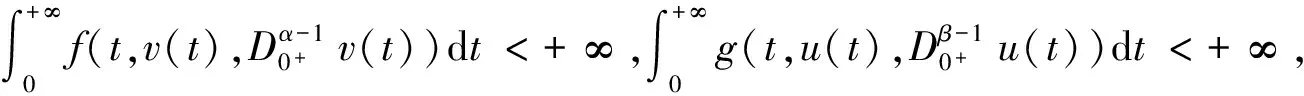
定义算子A(u,v)(t)=(A1(u,v)(t),A2(u,v)(t)), 其中

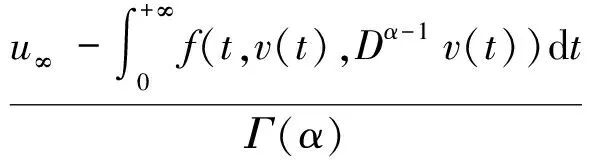
(3)

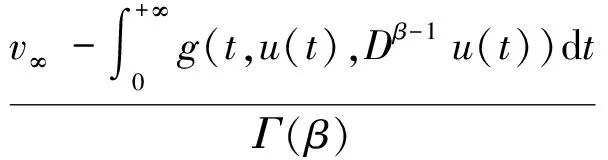
(4)

则边值问题(1)(2)的解等价于算子A的不动点.

证明利用引理1和边界条件(2), 易得.

2 主要结果

下面给出本文的主要定理,所用的不动点定理为Schauder不动点定理:

定理1 假设f,g∈C(J×R×R,R),条件(H)满足,则边值问题(1)(2)至少存在一个解.

证明由(3)(4)易知

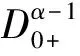
(5)

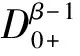
(6)

我们分3步证明:

(i) 取

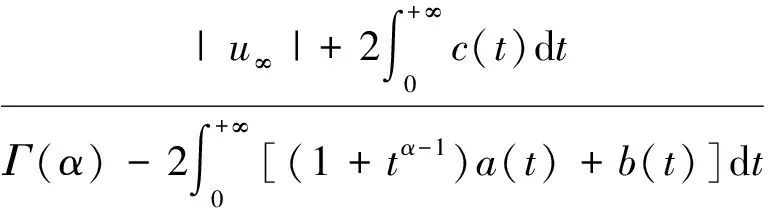
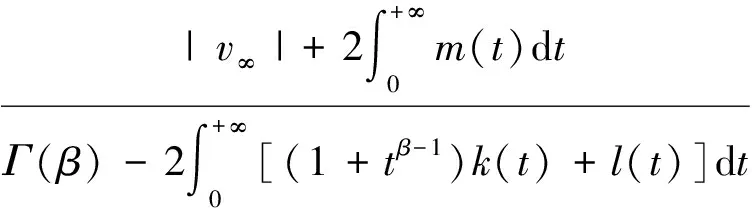
令R=max{R1,R2},U={(u(t),v(t))∈E:‖(u(t),v(t))‖E≤R},则A:U→U.

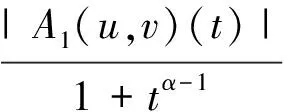
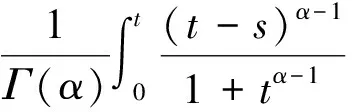
(7)

(8)

故‖A(u,v)(t)‖E≤R

(ii) 令V是U的子集, 下证AV是相对紧的

令I⊂J是紧子区间,t1,t2∈I,t1lt;t2,则对任意的(u,v)∈V,我们有

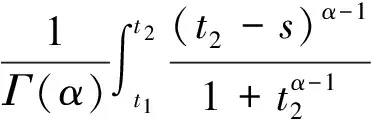
(9)

又

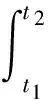
(10)

由条件(H),

故对任意给定的εgt;0,存在常数L1gt;0,使得

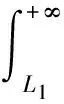
(11)

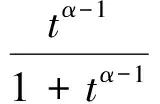
(12)

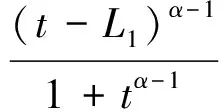
(13)

选取Tgt;max{T1,T2},则对t1,t2≥T

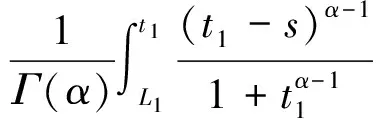
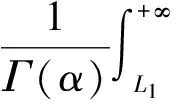
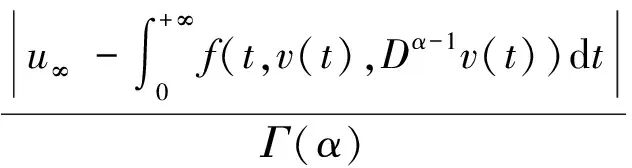
另外有

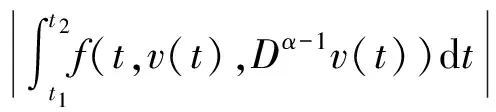
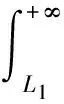
则由引理2知AV相对紧.

(iii) 我们验证算子A的连续性

设((un(t),vn(t)),(u(t),v(t))∈U,且‖un-u‖X2→0,‖vn-v‖X1→0,则由(3)～(6)和条件(H),有

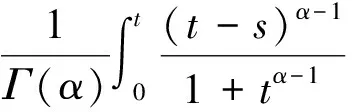
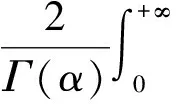
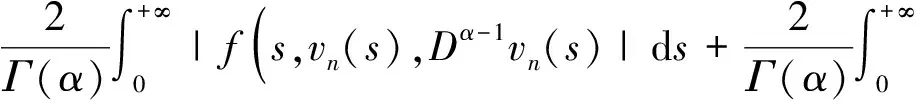
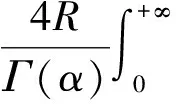
以及

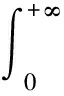
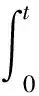
故由Lebesgue控制收敛定理知算子A是连续算子.综上,由Schauder不动点定理,可得边值问题(1),(2)在U中至少有一个解.

[1] Argarwal R P, O’Regan D. Infinite Interval Problems for Differential,Difference and Integral Equations?[M].Kluwer Academic, 2001.

[2] Bai Z B, Lv H S. Positive solutions for boundary value problem of nonlinear fractional differential equation?[J].J Math Anal Appl, 2005,311: 495-505.

[3] Su X. Boundary value problem for a coupled system of nonlinear fractional differential equations?[J].Appl Math Lett, 2009, 22: 64-69.

[4] Yang L,Chen H B. Unique positive solutions for fractional differential equation boundary value problem?[J].Appl Math Lett, 2010, 23: 1095-1098.

[5] Kilbas A A, Srivastava H M, Trujillo J J.Theory and Applications of Fractional Differential Equations?[M].Amsterdam, Elsevier B V, 2006.

[6] Arara A, Benchohra M, Hamidi N. Fractional order differential equations on unbounded domain?[J].Nolinear Anal, 2010, 72: 580-586.

[7] Zhao X K, Ge W G.Unbounded solutions for a fractional boundary value problem on the infinite interval?[J].Acta Appl Math, 2010, 109: 495-505.

[8] Su X, Zhang S Q.Unbounded solutions to a boundary value problem of fractinal order on the half-line?[J].Compu Math Appl, 2011, 61: 1079-1087.

[责任编辑：李春红]

ExistenceResultforaCoupledSystemofFractionalOrderBoundaryValueProblemontheHalf-line

ZHU Si-nian, WANG Gang

(College of Science China University Mining and Technology, Xuzhou Jiangsu 221008, China)

This paper deals with a boundary value problem of fractional order differential equation with the nonlinear term dependent on a fractional derivative of lower order on the semi-infinite interval.An appropriate criteria is established,such that we can use Schauder fixed point theorem to obtain the existence result for solution.

fractional order; infinite interval; fixed point theorem; boundary value problem

O175.8

A

1671-6876(2011)02-0099-07

2011-01-20

朱思念(1986-), 男, 山东济宁人, 硕士研究生, 研究方向为微分方程边值问题.