戴 勇，王萍姝

（1.黔南民族师范学院数学系，贵州都匀558000；2.青海民族大学数学与统计学院，青海西宁810007）

关于平面Bonnesen型不等式的注记

戴 勇1，王萍姝2

（1.黔南民族师范学院数学系，贵州都匀558000；2.青海民族大学数学与统计学院，青海西宁810007）

在原有Bonnesen型不等式的基础上，推导出一些Bonnesen型不等式，并给出其简单证明.关键词：等周不等式；平面凸闭曲线；Bonnesen型不等式

1 背景知识

最著名的几何不等式是以下的等周不等式:

等周不等式 设C是长度为L的平面简单闭曲线，A是C所围成有界区域的面积，则：

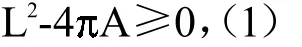
等号成立当且仅当C所围成区域为圆盘.

1870年K.Weierstrass第一个用变分法给出等周不等式严格的证明；1902年A.Hurwitz、1939年E.Schmidt应用级数法给出非常巧妙的证明；1904年Crore、1915年Frobenius、1919年H.Liebmann等也分别给出严格的证明；1955年 A.Santalo、W.blaschke、E.Steinitz、Bonnesen 等用积分几何思想证明了等周不等式；苏步青、陈省身、吴大任、任德麟、项武义、张高勇、周家足等对等周不等式的研究也有重要贡献[1-5].

上世纪初，由Fujiwara、Bol先导出不等式[4]：

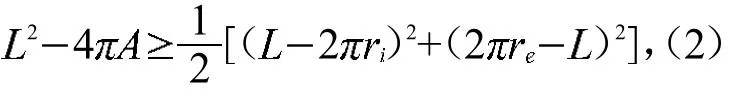
其中，L、A为一条凸闭曲线C的周长及所围区域的面积，为包含于C内的最大内接圆半径，为包含C的最小外接圆半径.

1924年 Bonnesen得到了以下加强的等周不等式[5]:

Bonnesen等周不等式（1924年） 设L、A为一条凸闭曲线C的周长及所围区域的面积，为包含于C内最大内接圆半径，为包含C的最小外接圆半径，则：

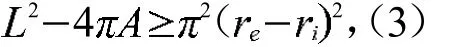
等号成立当且仅当C为圆周.

关于加强的等周不等式的推理与证明，已有诸多知名数学家给出了漂亮的结果[6-8].

本文在原有Bonnesen型不等式研究的基础上推出以下结果，并给出其简单证明.

2 主要结论与证明

定理1设C是周长为L的平面凸闭曲线，A为C所围成有界区域的面积，为C所围区域的最大内接圆半径，为包含C的最小外接圆半径，则:

推论1 设C是周长为L的平面凸闭曲线，为C所围成有界区域的面积，为C所围区域的最大内接圆半径，为包含C的最小外接圆半径，则:

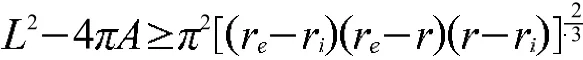
定理2 设C是周长为L的平面凸闭曲线，A为C所围成有界区域的面积，为C所围区域的最大内接圆半径，为包含C的最小外接圆半径，则:

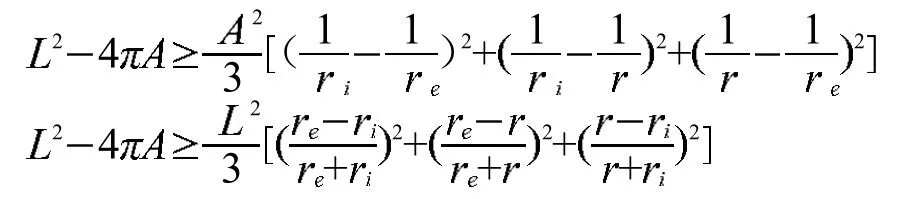
推论2 设C是周长为L的平面凸闭曲线，A为C所围成有界区域的面积，为C所围区域的最大内接圆半径，为包含C的最小外接圆半径，则:

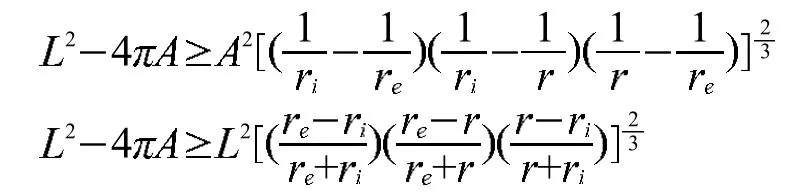
为了证明定理1、推论1、定理2及推论2，首先，我们有下列引理[6-8]：

引理1 设C是周长为L的平面凸闭曲线，A为C所围成有界区域的面积，为C所围区域的最大内接圆半径，re为包含C的最小外接圆半径，则

引理1的证明[6-7].

由引理1我们可得

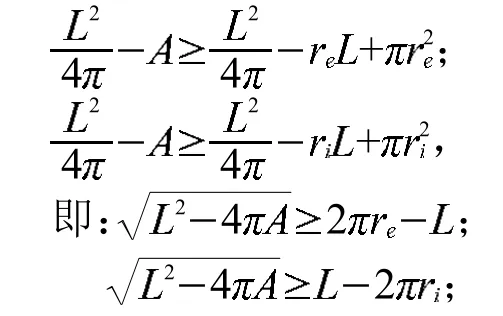
不等式两边取平方，化简整理得到Bonnesen等周不等式：

又由引理1可得：

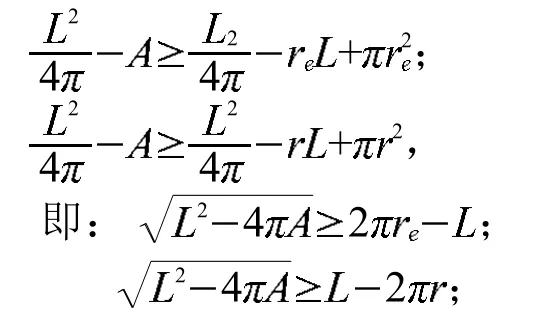
不等式两边取平方，化简整理得到Bonnesen型等周不等式：

不等式两边取平方，化简整理得到Bonnesen型等周不等式：

于是我们得到以下Bonnesen型不等式：

引理2 设C是周长为L的平面凸闭曲线，A为C所围成有界区域的面积，为C所围区域的最大内接圆半径，为包含C的最小外接圆半径，则：

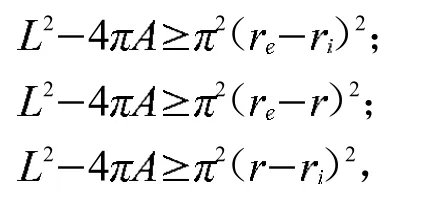
引理3[7]设C是周长为L的平面凸闭曲线，A为C所围成有界区域的面积，为C所围区域的最大内接圆半径，为包含C的最小外接圆半径，则：

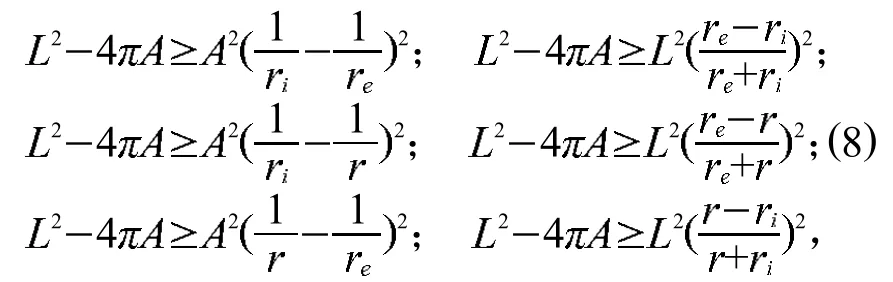
由（5）式、（6）式和（7）式相加，我们可得：

由引理3中左边三式相加，右边三式相加，分别可得：

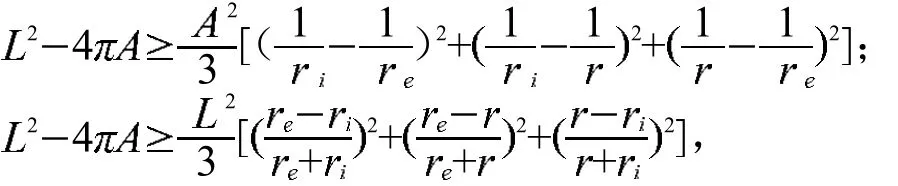
再利用均值不等式可得：

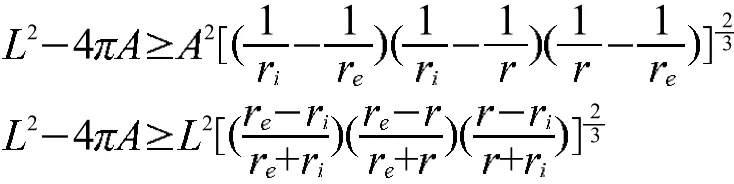
[1]Burago Y D,Zalgaller V A.Geometric In equalities[M].BerLin Heidelberg:Springer-Verlag,1988.

[2]Do Carmo M P.Differential Geometry of Curves and Sur faces[M].Beijing:China Machine Press,2005.

[3]OssermanR.Bonnesen-styleIsoperimetric Inequality[J].Amer Math Monthly,1979,（86）:1-29.

[4]Ren D L.Topics in Integral Geometry[M].Singapore:Word Scientific,1994.

[5]Santalo L A.Integral Geomtry and Geomtric Probabiliy[M].MA:Addison-Wesley,1976.

[6]Zhou J Z,Cheng F.The Bonnesen-type In equalities in a Plane of Constant Curvature[J].Journalof Korean Math.Soc.2007,44(6):1363-1372.

[7]Zhou J Z.Plan Bonnesen-type Inequalities[J].Acta Math Sinica,Chinese Series,2007,50(6):1397-1402.

[8]Zhou J Z,Ren D L.Geometric Inequalities-Form Integ ralGeometryPointofView[J].Acta Math-ematicaScient ia,2010,30(5):1322-1339.

（责任编辑：朱 彬）

DAI Yong1，WANG Ping-shu2
(1.Department of Mathematics,Qiannan Normal College for Nationalities,Duyun 558000,China;2.School of Mathematics,Qinghai University for Nationalities,Xining 810007,China)

On the basis of the originalBonnesen-type inequalities,this paper essays to deduce some bonnesen-type inequalities which have been exemplified.

isoperimetric inequality;closed planar convex curve;bonnesen-type inequality

0186.5

A

1009-3583（2011）-01-0088-02

2010-11-04

黔南民族师范学院科研基金资助项目(QNSY0906)

戴勇，男，贵州安顺人，黔南民族师范学院数学系副教授，主要从事凸几何与几何不等式研究。