黄浪扬

（华侨大学数学科学学院，福建泉州362021）

非线性“Good”Boussinesq方程的显式多辛格式

黄浪扬

（华侨大学数学科学学院，福建泉州362021）

对非线性“Good”Boussinesq方程的一个多辛方程组进行数值离散，导出方程的离散多辛守恒律，得到一个与此数值离散方法等价的，新的7点显式多辛格式.通过孤立波的数值模拟试验表明，所构造格式既能很好地模拟单孤立波运动的波形，又能很好地模拟双孤立波的碰撞过程，可有效地模拟原孤立波的时间演化，具有长时间的数值稳定性.

非线性“Good”Boussinesq方程；多辛方程组；显式多辛格式；多辛守恒律；孤立波试验

近年来，多辛数值方法的研究［1－3］受到了广泛的重视，它涉及了流体力学、量子力学、结构力学等许多研究领域.文［4］构造了非线性“Good”Boussinesq方程的一个隐式的15点多辛Preissmann格式.本文进一步提出此方程的一个新的7点显式多辛格式.

1 多辛方程组形式

考虑满足周期边界条件的非线性“Good”Boussinesq方程utt＝－uxxxx＋uxx＋（G′（u））xx.（1）式（1）中，G（u）：R→R是某个非线性光滑函数.根据文［1］引入的多辛积分的概念，引入正则动量v＝ux，ut＝px，wx＝p，则式（1）可改写成多辛方程组的形式，有

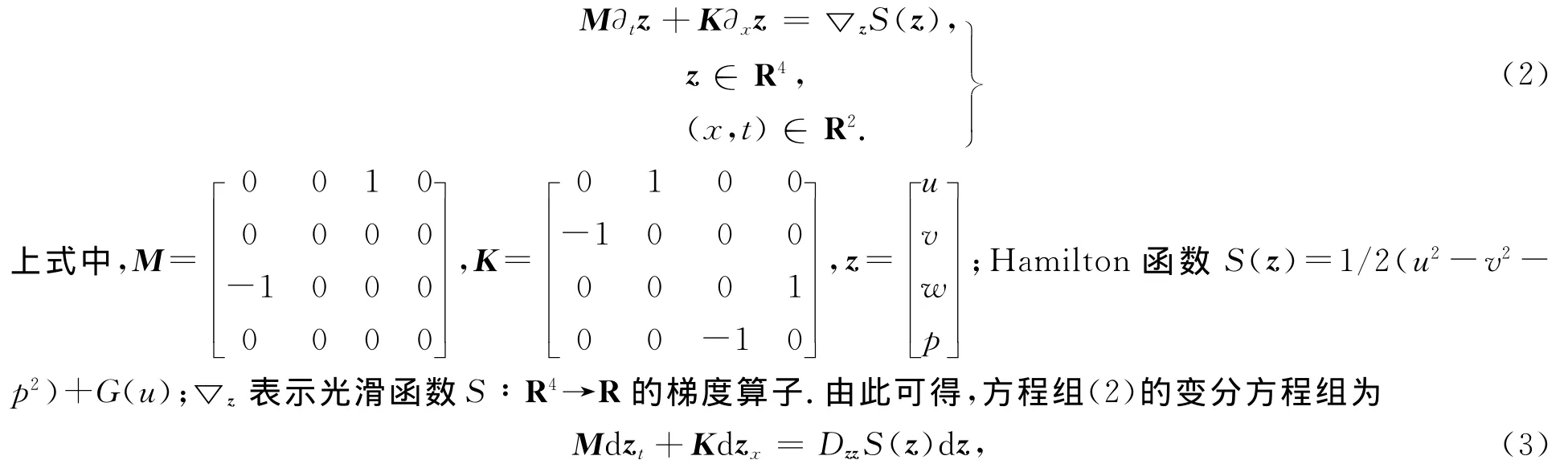
对变分方程组（3）两边与d z作外积运算，可得重要的多辛守恒律为

式（4）中，Λ为外积算子.求解多辛方程组（2）的数值方法，可表示为

式（5）中，zi，j＝z（xi，tj）＝z（i·h，j·τ），h和τ分别是空间步长和时间步长，∂i，jt，∂i，jx分别为算子∂t，∂x的离散.Bridges等［1］称能保持多辛守恒律（5）的离散形式的格式为多辛格式.

2 显式多辛格式

首先考察一些差分算子的性质［3］.定义向前差分算子Dtfj＝（fj＋1－fj）／τ，Dxfi＝（fi＋1－fi）／h，易得推广的Leibniz法则，有

以上性质对t方向也成立，只要算符运算是双线性的，离散的Leibniz法则就成立.例如外积运算，此时f，g是一形式.

对多辛方程组（2）的分量形式进行离散，可得到其离散格式，有

定理1 格式（8）是多辛格式，它满足离散多辛守恒律

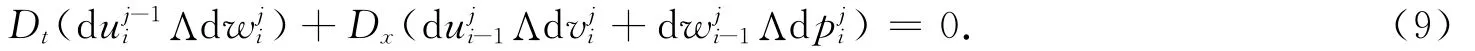
证明 式（8）对应的变分方程组为

用d uji外积式（10）的第1个方程，可得

3 数值例子

取G（u）＝u3／3，则非线性“Good”Boussinesq方程（1）的精确孤立波解为

对于非线性“Good”Boussinesq方程的显式多辛格式，采取在有限区域I＝（XL，XR）上设置人工边界和周期边界条件的方法进行数值模拟.即对人工边界XL和XR取得足够远，以满足周期边界条件.由于格式（15）是三层格式，所以为简便起见，格式初始时的第1层和第2层的值均取精确值.

3.1 单孤立波的模拟

在孤立波解式（16）中，取振幅A为0.5，初相ξ0为0，且XL＝－50，XR＝50，时间步长τ为0.01，空间步长h为0.5.显式多辛格式（15）在t∈［0，100］时，单孤立波传播的模拟结果如图1所示.

3.2 同向双孤立波的模拟

在孤立波解式（16）中，取两个不同振幅、不同初相的孤立波分别进行数值模拟试验.当振幅A分别为1，0.25，相应的初相ξ0分别为－60，－80，此时XL＝－100，XR＝100，时间步长τ为0.01，空间步长h为0.5.显式多辛格式（15）模拟双孤立波同向传播时，其碰撞分离的模拟结果如图2所示.

图2 双孤立波的碰撞过程Fig.2 Collision process of two solitons

图1 单孤立波的传播Fig.1 Propagation of soliton

4 结论

由图1（数值模拟试验均计算10 000步，下同）可知，显式多辛格式（15）能很好地模拟单孤立波运动的波形，不出现振荡现象.由图2可知，显式多辛格式（15）同样能够很好地模拟双孤立波的碰撞过程，碰撞后，两个孤立子保持原来的形状及速度传播，好象碰撞没有发生过似的.

由此可见，所构造的显式多辛格式能够成功、有效地模拟原孤立波的时间演化，具有长时间的数值稳定性.由于多辛格式（15）是显式的，因此计算量比隐式的15点多辛Preissmann格式大大减小，数值模拟结果与理论相符.

［1］ BRIDGES T J，REICH S.Multi－symplectic integrators：Numerical schemes for Hamiltonian PDEs that conserve symplecticity［J］.Physics Letter（A），2001，284（4－5）：184－193.

［2］ 黄浪扬.广义Pochhammer－Chree方程的多辛Fourier拟谱格式及孤立波试验［J］.华侨大学学报：自然科学版，2008，29（3）：468－471.

［3］ 王雨顺，王斌，秦孟兆.偏微分方程的局部保结构算法［J］.中国科学：A辑，2008，38（4）：377－397.

［4］ 曾文平，黄浪扬，秦孟兆.“Good”Boussinesq方程的多辛算法［J］.应用数学和力学，2002，23（7）：743－748.

Explicit Multi－Symplectic Scheme for Nonlinear“Good”Boussinesq Equation

HUANG Lang－yang
（School of Mathematical Sciences，Huaqiao University，Quanzhou 362021，China）

By discretizing the multi－symplectic systems of the nonlinear“Good”Boussinesq equation，we have derived the discretized multi－symplectic conservation laws.A new seven－point explicit multi－symplectic scheme which is equivalent to the discretized method is obtained.It is showen that the scheme constructed in this paper has excellent long－time numerical behavier by numerical experiments.

nonlinear“Good”Boussinesq equation；multi－symplectic systems；explicit multi－symplectic scheme；multisymplectic conservation laws；solitary wave experiments

O 241.82

A

（责任编辑：陈志贤 英文审校：张金顺，黄心中）

1000－5013（2011）01－0100－03

2009－04－11

黄浪扬（1974－），男，副教授，主要从事偏微分方程数值解法的研究.E－mail：hly6＠163.com.

国家自然科学基金资助项目（10901074）；福建省自然科学基金资助项目（Z0511029）