彭惠芬，孟广伟，周立明，李 锋

（1.吉林大学机械科学与工程学院，130022 长春，phfdaqing@163.com;2.东北石油大学机械科学与工程学院，163318 大庆黑龙江）

含裂纹结构的区间B样条小波模糊有限元分析

彭惠芬1，2，孟广伟1，周立明1，李 锋1

（1.吉林大学机械科学与工程学院，130022 长春，phfdaqing@163.com;2.东北石油大学机械科学与工程学院，163318 大庆黑龙江）

为了解决工程问题中材料和载荷的不确定性给含裂纹结构数值分析带来的困难，提高数值计算的精度和效率，将模糊理论与小波有限元相结合，提出了基于区间B样条小波(B-spline wavelet on the interval，BSWI)模糊有限元分析法.该方法将哑节点断裂单元镶嵌到含裂纹结构的小波有限元模型中，建立了含裂纹结构的小波有限元模型，推导了小波有限元模糊平衡方程，并采用λ水平截集及分解定理求解模糊平衡方程;在此基础上，利用虚拟裂纹闭合法计算了不同裂纹长度下应力强度因子隶属函数值，并将计算结果与解析解进行了比较.结果分析表明该方法可用较少单元更为真实、准确地反映结构响应的变化情况，为工程实际中实现含不确定参数的断裂数值分析提供了一种新途径.

区间B样条小波;裂纹;模糊数;应力强度因子;有限元

现有的断裂力学数值分析方法大多都是基于传统有限元模型的.传统有限元理论对裂纹等奇异性问题，存在计算精度低和效率下降的弊端.近年来，人们提出了一些新的有限元法，如有限差分法［1］、边界元法［2－3］和无网格法［4－5］等，但由于缺少相应软件的支持，使这些数值方法的发展受到了限制.

小波有限元法(Wavelet Finite Element Method，WFEM)是近几年发展起来的一种新的数值分析方法.以小波函数或小波尺度函数作为插值函数，充分利用小波尺度函数的多分辨特性，可根据实际需要任意改变分析尺度，具有算法稳定性好、计算精度和效率高的优点.因此，在裂纹等奇异性问题数值计算方面具有诱人的优越性.目前，小波有限元法研究对象基本上是确定性问题.然而，在实际工程结构中，由于各种因素的影响，使得结构的物理参数、几何参数及载荷等具有不确定性，从而导致结构的响应也具有不确定性，这种不确定性需要用模糊理论来进行研究［6－7］.本文针对工程实际中几何参数及载荷等不确定性裂纹结构的有限元分析问题，提出了基于BSWI模糊有限元分析法，建立了BSWI有限元模糊断裂分析模型，采用区间数分解方法求解模糊平衡方程，基于输入材料和载荷模糊数的隶属函数，利用虚拟裂纹闭合法，计算并分析了含裂纹结构响应量的可能性分布.数值算例证明了该方法切实可行，并具有较高的计算精度.

1 BSWI单元构造

采用BSWI尺度函数的张量积插值构造单元，位移函数表示为

式中:Φ1，Φ2分别为m阶j尺度空间的n(n=2j+m －1)个一维BSWI尺度函数［8］;p、q分别为待求小波系数列向量;ε，η分别为单元局部坐标.局部坐标与整体坐标关系为

式中:x1，y1分别为整体坐标下单元起始坐标;Lex为单元长度;Ley为宽度.

单元节点位移列阵为

将各节点坐标和位移代入式(1)和式(2)，即得:

由弹性力学知，平面应力问题的势能泛函为

式中:Ωe为单元求解域;t为单元厚度;F={fx，fy}T为体力向量;p={px，py}T为面力向量;R={u，v}T为位移场向量;D为弹性矩阵;ε为应变矩阵，其中

式中:E，μ分别为材料的弹性模量和泊松比.

将式(3)、式(5)和式(6)联立，由变分原理，令δΠp=0，可得单元刚度矩阵为

2 BSWI断裂单元构造

BSWI哑节点断裂单元(构造如图1所示)，是用来从小波有限元分析结果中提取相关信息，进而计算裂纹尖端后面的张开位移和裂纹尖端前面的虚拟裂纹扩展量［9－10］.

沿裂纹方向，哑节点断裂单元从两侧的小波单元中共提取5个节点:节点1和节点2对应于裂纹尖端，并用特殊刚度的弹簧连接;节点3和节点4在裂纹尖端的后面;节点5在裂纹尖端的前面.在实际应用时，节点1和节点2，节点3和节点4的坐标分别是重合的.

图1 哑节点断裂单元及节点位移矢量

设Kx和Ky分别为x和y方向的弹簧刚度，由图1可知，裂纹尖端垂直节点力为

裂纹尖端后面的张开垂直位移为

裂纹前面的虚拟扩展为

3 BSWI模糊有限元分析

式中:Em为的主值，其值与不考虑弹性模量模糊性时的E值相同;EL，ER分别为的左、右展形.

根据式(7)，相应地，小波模糊单元刚度矩阵为

将式(14)代入式(12)得:

将式(15)代入式(13)得:

式中［Km］e与式(7)普通 BSWI单元刚度矩阵相同.

式中:Fm为的主值，FL，FR分别为的左、右展形.

假设弹簧连接裂尖节点i和i+1，组集哑节点断裂单元和各BSWI模糊单元的刚度矩阵可得含裂纹结构总模糊刚度矩阵为

L－R型模糊结构平衡方程为

对模糊结构小波有限元平衡方程作λ水平截集，可得区间方程:

根据区间数运算法则和区间数分解形式的唯一性，λ水平截集下结构区间方程的解［11］为

4 BSWI虚拟裂纹闭合法

虚拟裂纹闭合法是用于二维断裂参数问题计算的一步分析法，具有精度高、方法简单的优点.本文针对I型裂纹断裂问题进行讨论，但思路和方法适用于其他断裂模式.如图2所示，将裂纹从α扩展到α+Δα所需要的功与将裂纹从α+Δα闭合到α所需要的功是相等的.

图2 虚拟裂纹闭合法

在虚拟裂纹线上裂纹尖端节点力在节点位移上做功为

假设虚拟裂纹尖端后面的张开位移和初始裂纹尖端后面的张开位移近似相等，式(22)改写为

数值实验表明虚拟裂纹闭合法对有限元网格尺寸并不敏感，因此，I型裂纹能量释放率G1可近似表达为

式中B为裂纹体的厚度.

对于各向同性均匀线弹性材料而言，应力强度因子KI和能量释放率GI的关系为

当λ取遍［0，1］中的一切值后，根据模糊分解定理可得结构模糊应力强度因子为

若只取有限个λ值进行计算，则:

5 算例分析

如图3所示，共线双边裂纹单向拉伸平板.其中:L=2 m，W=2 m，裂纹长度a，板厚t=0.01 m，弹性模量 E=(210，0.04，0.04)LRGPa，泊松比μ =0.3，σ =(0.2，0.01，0.01)LRMPa，计算时，弹性模量、载荷均为L－R型模糊数，其隶属函数取为线性函数为

假设为平面应力问题，试用基于BSWI小波有限元的模糊虚拟裂纹闭合法计算其应力强度因子.

图3 裂纹板单向拉伸

为更好地利用BSWI有限元虚拟裂纹闭合法，考虑结构几何和载荷的对称性，取该结构1/2作为计算模型，在其底部施加对称边界条件，采用2个二阶三尺度区间B样条小波(BSWI23)和1个哑节点断裂单元求解.

表1给出了当隶属度为1.0时，采用2个BSWI23单元的模糊虚拟裂纹闭合法计算不同裂纹长度下应力强度因子与解析解的相对误差.从表1中可看出最大相对误差值为1.583%，说明本文提出的计算方法切实可行的，并可用较少单元获得较高计算精度.

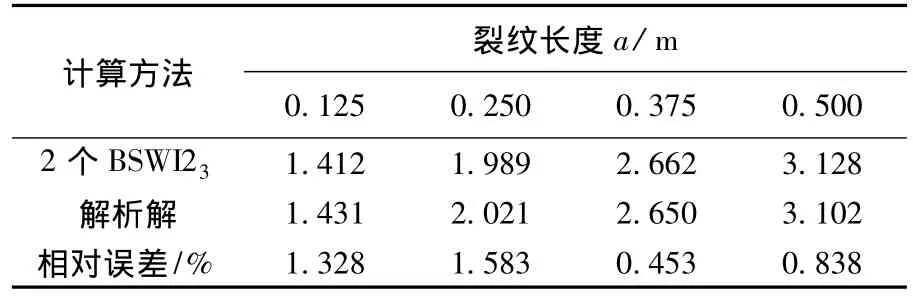
表1 隶属度为1.0时模糊算法与解析解的相对误差

表2给出了不同裂纹长度α下的应力强度因子KI隶属函数值.由表2看出不同隶属度下应力强度因子随裂纹长度变化的关系.

图4，5分别为裂纹面上距裂尖r=0.125，0.250 m处垂直位移v的隶属函数图.由于选取左、右基准函数L(x)，R(x)相同，垂直位移v分布均为中心对称分布;由图4，5可见，对于不同r值，当隶属度较低时，垂直位移v的变化区间较大，当隶属度较高时，垂直位移v变化区间较小，当隶属度为1.0时，左右端点值均相等，分别为v0.125=4.569 6×10－5m和v0.250=6.446 6 ×10－5m，结果与确定性小波有限元结果一致.由此看出，利用本文建立的区间B样条小波有限元模糊虚拟裂纹闭合法对含裂纹结构进行断裂分析比确定性小波有限元分析更能全面反映结构响应的真实变化情况.

表2 不同裂纹长度下应力强度因子隶属函数值 105Pa·m1/2

图4 裂纹面上距裂尖r=0.125 m垂直位移v隶属函数

图5 裂纹面上距裂尖r=0.250 m垂直位移v隶属函数

6 结 论

1)将本文方法的计算结果与解析解进行了比较，结果表明:当隶属度为1.0时，不同裂纹长度下，应力强度因子隶属函数值最大相对误差为1.583%.验证了该方法在解决含有不确定性参数的裂纹结构有限元分析方面的可靠性.

2)利用本方法计算了不同裂纹长度和隶属度下的应力强度因子KI隶属函数值.结果表明:对于不同r值，当隶属度较低时，垂直位移v的变化区间较大，当隶属度较高时，垂直位移v变化区间较小，当隶属度为1.0时，左右端点值均相等.由此看出，本文建立的计算方法对含裂纹结构进行断裂分析比确定性有限元分析法更能全面反映结构响应的真实变化情况.

3)小波有限元与传统有限元相比，在计算裂纹等奇异性问题方面可用较少单元和自由度数，获得较高计算精度和效率，因此，在数值计算方法上为求解具有材料和载荷不确定性的裂尖奇异性问题提供了一种可行的途径.

［1］ZHANG Yang.A finite difference method for fractional partial differential equation［J］.Applied Mathematics and Computation，2009，215(2):524－529.

［2］程长征，牛忠荣，叶建乔.边界元法计算浅表面裂纹应力强度因子［J］.合肥工业大学学报(自然科学版)，2009，32(4):503－507.

［3］SUN Yuzhou，WANG Jinyan，XU Junfeng.Boundary element method for the plane elastic problem with cracks［J］.Journal of Zhong yuan Institute of Technology，2004，15(5):46－54.

［4］张雄，刘岩，马上.无网格法的理论及应用［J］.力学进展，2009，39(1):1－36.

［5］RAO B N，RAHMAN S.Probabilistic fracture mechanics by Galerkin meshless methods-Part I:Rates of stress intensity factors［J］.Computational Mechanics，2002，28(5):351－364.

［6］苏静波，卲国建.基于区间分析的工程结构不确定性研究现状与展望［J］.力学进展，2005，35(3):338－344.

［7］RASHID M K，AL-ARAIMI S A.Fuzzy algorithm and structural stiffness in error attenuation of intelligent toolpost［J］.Journal of Intelligent Manufacturing，2005(16):277－286.

［8］何正嘉，陈雪峰，李兵，等.小波有限元理论及其工程应用［M］.北京:科学出版社，2006:40－42.

［9］XIE D.Damage progression in tailored laminated panels with a cutout and delamination growth in sandwich panels with tailored face sheets［D］.Clemson:Clemson U-niversity，2002.

［10］XIE D，Jr BIGGERS S B.Progressive crack growth analysis using interface element based on the virtual crack closure technique［J］.Finite Elements in Analysis and Design，2006，42(11):977－984.

［11］肖盛燮，王平义，吕恩琳.模糊数学在土木与水利工程中的应用［M］.北京:人民交通出版社，2004:349－368.

Fuzzy finite element analysis of B-spline wavelet on the interval of structure with cracks

PENG Hui-fen1，2，MENG Guang-wei1，ZHOU Li-ming1，LI Feng1

(1.College of Mechanical Science and Engineering，Jilin University，130022 Changchun，China，phfdaqing@163.com;2.College of Mechanical Science and Engineering，Northeast Petroleum University，163318 Daqing，China)

To overcome the difficults caused by uncertainties of material and load in numerical analysis of structure with cracks and to improve the accuracy and efficiency of numerical calculation，a fuzzy finite element analysis method of B-spline wavelet on the interval(BSWI)is put forward by combing the fuzzy theories with wavelet finite element.Fracture elements of dummy nodes are embedded into the wavelet finite element model with cracks，fuzzy equilibrium equations on the basis of finite element of BSWI are established，and the fuzzy equilibrium equations are solved by using λ level set and decomposition theorem.Subsequently，the membership function values of stress intensity factor with different crack lengths are calculated by using virtual crack closure technique，and the calculated results are compared with analytical solution.The analysis results show that the proposed method can accurately reflect changes in structural response with fewer elements and can be a new way for engineering fracture analysis of complex structures with uncertainties.

BSWI;crack;fuzzy numbers;stress intensive factor;finite element method

O242;TB115

A

0367－6234(2011)09－0134－05

2010－12－20.

高等学校博士学科专项科研基金资助项目(20060183063);吉林省科学技术厅基金资助项目(20090540);吉林大学“985工程”资助项目.

彭惠芬(1969—)，女，博士研究生，副教授;

孟广伟(1959—)，男，教授，博士生导师.

(编辑 张 红)