宋占杰，叶培新

(1. 天津大学理学院，天津 300072；2. 南开大学数学学院，天津 300071)

众所周知，前苏联数学家 Bernstein[1]于 1911年构造了著名的Bernstein多项式，即

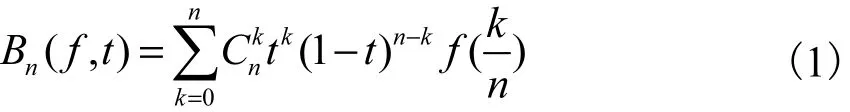
从式(1)可以看出，采样值所对应的核函数正好对应概率论中的二项分布．对于离散型随机变量，概率论中有3个重要分布：二项分布(binomial distribution)、泊松分布(Poisson distribution)和负二项分布(negative binomial distribution). 这 3个概率分布分别于 1713、1837和 1654年给出，后来诸分布又都被数学家用来构造相应的多项式用于逼近确定性信号(函数).

首先，瑞士数学家 Bernoulli在 1713年出版了《猜算术》一书，介绍了著名的伯努利实验.以独立实验为基础，考虑每次实验成功的概率为p，失败的概率为 q =1- p，则进行n次实验，成功 k ( k = 0 ,1,⋅⋅⋅,n)次的概率为

后来发现这正好对应二项式展开式，故称为二项分布．法国数学家 Poisson于 1837年出版了他的概率著作[3]，首次给出了泊松分布，作为二项分布的近似，nPn→λ，事件发生k( k= 0 ,1,⋅⋅⋅)次的概率为

负二项分布发现实际上早一些.概率论创始人之一，法国数学家 Pascal于1654年前后研究杨辉三角(亦称帕斯卡三角)，研究等到第 n ( n = k , k + 1,⋅⋅⋅)次实验才成功k次的概率时发现了负二项分布，也正是这一工作引导牛顿发现了分数和负指数的函数二项展开式.但后来美籍匈牙利数学家 Polya进行过深入研究，因此负二项分布除了称为 Pascal分布外，也称为Polya分布.其分布率为

继Bernstein利用二项分布构造Bernstein多项式之后，Mirakian于 1941年利用泊松分布构造 Szasz-Mirakian 算子[4]为

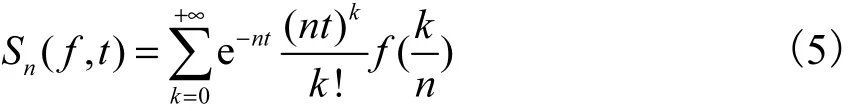
但是，Mirakian的思想长期未引起注意．1950年，匈牙利数学家 Szasz再次提出这一算子[5]，才引起世人的广泛关注.

利用负二项分布构造算子出现更晚，1957年Baskakov才构造出Baskakov算子[6]，即

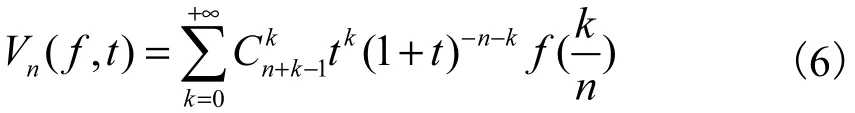
目前，世界各地研究这类算子的相关学术论文超过 2,000篇，许多结果发表在《Constructive Approximation》和《Journal of Approximation Theory》等国际著名的学术杂志．我国徐利治教授、郭竹瑞教授、郭顺生教授和陈文忠教授等人都做出过很好的研究工作．特别是郭顺生教授在 20世纪 80年代末将中心极限定理引入概率型算子逼近，得到了很好的逼近阶[7-10]，推动了这一方向的发展．尽管 20世纪 80年代末小波分析出现之后，这类经典概率型算子的研究有所降温，国内外许多学者转入研究以小波分析为逼近工具的非线性逼近，但线性算子的逼近仍具有基础性的作用．目前这类算子的各种变形算子的研究结果依然常见于国内外一些有名的学术杂志[10-19].一个挑战性的问题是如何将经典的算子逼近理论与相关的新兴学科交叉渗透从而为其发展提供新的增长点.笔者将试图给出解决这类问题的一个途径.

为了深入了解课程建设对于教学各方面的影响，我们选取了部分师生做了问卷调查，参与问卷的学生学习的课程中有的课程进行了课程资源建设，参与问卷的老师有课程建设的经历。问卷调查分析如下

1 Feller概率型算子与新型Feller概率型算子

在前人利用概率分布构造一些著名算子的基础上，国际著名概率专家 Feller[20]在 1966年提出了一大类概率型算子，包含了上述各类算子.

定义 1假设 Xn(n ≥ 1) 是一列随机变量列，其分布函数、数学期望和方差分别为 Fn,t(x)、E Xn=t和σn2( t)，其中 t为实连续参数.对定义在实数范围R上的连续函数f，称

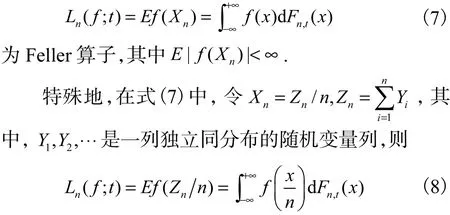
为一类特殊的 Feller算子.如果在式(8)中，Yi( i = 1 ,2,⋅⋅⋅)取概率论中3类常用分布，可得上述3类著名算子．

(1) 若 Y1服从参数为 t(0 ≤ t≤1)的0-1分布，即P( Y1= 1 )=1 - P ( Y1= 0 ) = t , 则 Zn服从二项分布，可以得到著名的Bernstein算子．

(2) 若 Y1服从参数为 t( t ≥ 0 )的 Poisson分布，即P( Y = k ) = ,k = 0 ,1,⋅⋅,则 Z 服从参数为 nt的Poisson分布，于是可得著名的Szasz-Mirakian算子．

(3) 若 Y1服从参数为 t(0 ≤ t≤1)的几何分布，即P( Y1= k ) = t ( 1 - t )k,k = 0 ,1,⋅⋅⋅,则 Zn服从参数为t的负二项分布，可得著名的Baskakov算子.

命题1[21]若在式(7)中，(t) = 0 ,对任何连续有界的函数 f , Ln(f, t) → f( t)；而且若σn2( t )→0是一致的，f ( t)是一致连续的，则 Ln(f, t)也一致收敛于f( t).

由此可得类似控制收敛定理的结论.

命题 2(Khan[21]，引理 2)若在式(7)中，σn2(t)≤g( t), g( t)是关于分布函数 G ( t)可积的，命题 1条件成立，则有对任何连续有界的函数 f , Ln(f, t)→f( t)；而且若σn2( t) → 0 是一致的，f ( t)是一致连续的，则 Ln(f, t)也一致收敛于 f ( t).

此外，对任何连续有界的函数 f ( x)，前苏联数学家Korovkin[22]在1959年也曾给出一个重要的结果.

命题 3(Korovkin[22])若正线性算子列 Sn:C [ a,b ] → M [ a , b]([a , b]上有界实函数空间)满足

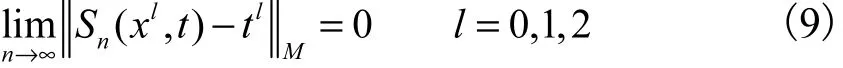
且对 t ∈[a , b]一致成立，f∈M( R)，则

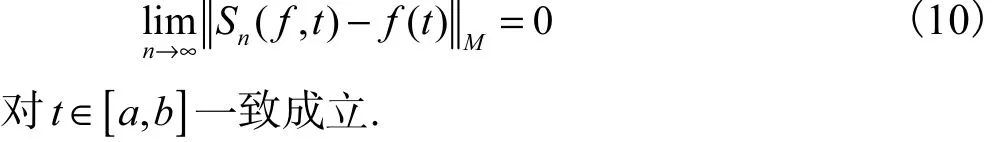
显然，Korovkin给出的算子包含了前言介绍的若干经典概率型算子.

从Bernstein构造著名的Bernstein多项式开始，长达近一个世纪从事逼近论研究的数学家们仅仅是考虑用各类算子来逼近确定性信号 ()F x，很少有人考虑用算子逼近随机过程 ()X t．2000年，Pogany[23]意识到这项工作是可行的，至今没有引起广泛注意.2006年，Kowalski[24]建立了 Bernstein多项式与布朗运动的联系，但 Kowalski当时并未意识到有一大类算子可以逼近布朗运动和其他二阶矩过程．另外，由于布朗运动在物理学、金融分析等诸多领域有广泛的应用背景，同时在有限时间内布朗运动是特殊的二阶矩过程，因此笔者如下构造Feller-Random算子，以逼近二阶矩过程 ()X t是有意义的.

定义2假设 Xn(n ≥ 1) 是一列随机变量列，其分布函数、数学期望和方差分别为 Fn,t(t*)、E Xn=t和( t)，其中 t为实连续参数．对定义在实数范围R上的均方连续二阶矩过程 X ( t,ω)，若广义均方积分

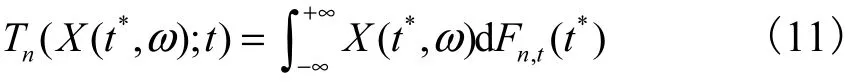
均方收敛，称 Tn( X( t*,ω);t)为Feller-Random算子．

此外，对于均方连续二阶矩过程，下述均方可积准则成立．

命题 4设 f ( t)是[a , b]上的连续函数，X ( t,ω)在[a , b]均方连续，则 f ( t) X( t)在[a , b]均方可积，且

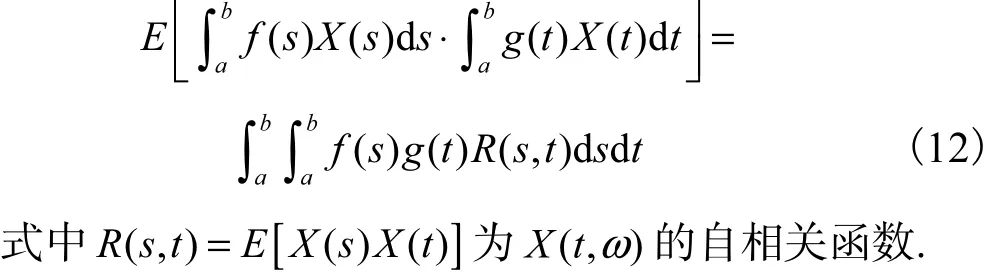
2 主要结果及其证明

由于对上述任意0ε＞，δ和*M 都是定值，利用命题4和傅比尼定理，有

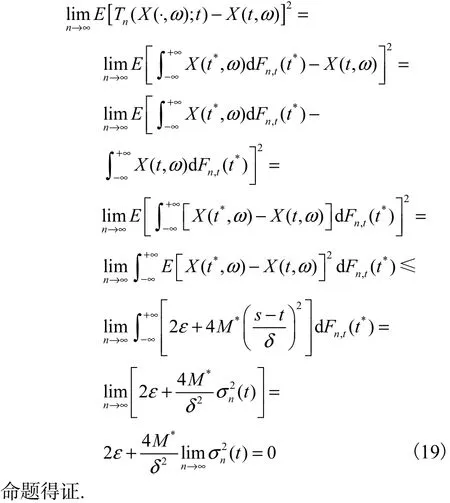
3 结 语

二阶矩过程是一类重要的随机过程，在物理学、生物学、通信与控制、系统工程与管理科学等方面都有广泛的应用．研究二阶矩过程模拟、分解、重构和逼近有一定的理论意义和应用价值．本文的研究结果表明，均方连续二阶矩过程可以由一大类概率型算子逼近在理论上是可行的，Kowalski[24]得到的第1个结论属于本文特例．在不远的将来，利用经典概率型算子的分析技巧去研究随机过程的逼近问题，将会是一个新的发展方向．

［1］Bernstein S. Dmonstration du Thorme de Weierstrass Fonde sur le Calcul des Probabilits[J].Communications dela Socit Math de Kharow，1913，2(13)：1-2.

［2］王国瑾，汪国昭，郑建民. 计算机辅助几何设计[M].北京：高等教育出版社-施普林格出版社，2001.

Wang Guojin，Wang Guozhao，Zheng Jianmin.Computer Aided Geometric Design[M]. Beijing：Higher Education Press-Springer，2001(in Chinese).

［3］Mirakian G M. Approximation of continuous functions with the aid of polynomials[J].Dokl Acad NaukSSSR，1941，31：201-205.

［4］Szasz O. Generalization of Bernstein's polynomials to the infinite interval[J].J Research Nat Bur Standards，1950，45：239-245.

［5］Baskakov V A. An instance of a sequence of linear positive operators in the space of continuous functions[J].Dokl Akad NaukSSSR，1957，113：249-251.

［6］Guo S. On the rate of convergence of the Durrmeyer operator for functions of bounded variation[J]. JApprox Theory，1987，51(2)：183-192.

［7］Guo S. On the rate of convergence the integrated Meyer-Konig and Zeller operators for functions of bounded variation[J].J Approx Theory，1989，56(3)：245-255.

［8］Guo S，Khan M. On the rate of convergence of some operators on functions of bounded variation[J].J Approx Theory，1989，58(1)：90-101.

［9］郭顺生. 关于SBK算子对有界变差函数的点态逼近度[J]. 科学通报，1986，31(20)：1521-1526.

Guo Shunsheng. On the rate of pointwise convergence of the SBK operators for functions of bounded variation[J].Kexue Tongbao，1986，31(20)：1521-1526(in Chinese).

［10］Chen W，Ditzian Z，Ivanov K. Strong converse inequalities for Bernstein-Durrmeyer operators[J]. J ApproxTheory，1993，75(1)：25-43.

［11］Chen W，Ditzian Z. Strong converse inequalities for Kantorovich polynomials[J].Constructive Approximation，1994，10(1)：95-106.

［12］Ditzian Z. Direct estimate for Bernstein polynomials[J].J Approx Theory，1994，79(1)：165-166.

［13］Ditzian Z，Felten M. Averages using translation induced by Laguerre and Jacobi expansions[J].Constructive Approximation，2000，16(1)：115-153.

［14］Ditzian Z，Totik V.Moduli of Smoothness[M]. New York：Springer-Verlag，1987.

［15］Felten M. Local and global approximation theorems for positive linear operators[J].J Approx Theory，1998，94(3)：396-419.

［16］Felten M. Direct and inverse estimates for Bernstein polynomials[J].Constructive Approximation，1998，14(3)：459-468.

［17］Guo S，Li C，Qi Q. Strong converse inequalities for Meyer-Konig and Zeller operators[J].J Math Anal Appl，2008，337(2)：994-1001.

［18］Guo S，Qi Q. Strong converse inequalities for Baskakov operators[J].J Approx Theory，2003，124(2)：219-231.

［19］Guo S，Zhang G，Liu G. Strong converse inequality for left Bernstein quasi-interpolants[J].Appl Math Letters，2009，22(2)：175-181.

［20］Feller W.An Introduction to Probability Theory and Its Applications(Ⅱ)[M]. New York：Wiley，1966.

［21］Khan R A. Some probabilistic methods in the theory of approximation operators[J].Acta Mathematica Hungarica，1980，35(1/2)：193-203.

［22］Korovkin P P. Linear Operators and Approximation Theory[M]. Gosizdat，Fizmatlit：Moscow，1959.

［23］Pogany T K. Some Korovkin-type theorems for stochastic processes[J].Theory of Probability and Mathematical Statistics，2000，61：153-158．

［24］Kowalski E. Bernstein polynomials and Brownian motion[J].The American Mathematical Monthly，2006，13(12)：856-886.