琚鑫 郑鹉

(首都师范大学物理系 北京 100048)

1 引言

单摆是物理学中一类重要的谐振子模型．无论是在经典物理，还是在量子物理，能否成功地求解谐振子问题，可以被认为是一个物理理论是否可行的判定标准之一.单摆还为人们开启了一条由线性物理学进入到非线性物理学的窗口．单摆这一简单的物理模型不仅包含了物理知识和物理规律，同时在求解单摆问题的过程中，很多科学方法和思维模式的使用，使得单摆无论是在中学教学中，还是在大学教学中都占据了极为重要的地位．

单摆中的一个重要的研究课题就是单摆的周期．如何精确地从理论上计算和从实验上测量周期就成为一个需要深入研究的问题．在理论计算方面，目前教材中流行的方法基本都是采用线性近似，即对摆角θ的正弦值做线性处理，亦即sinθ≈θ，将非线性的微分方程变成线性微分方程，于是可以得到单摆的振动周期为

(1)

其中l是摆长，g是重力加速度．

笔者注意到，现行高中物理新课程教材[1]中，有这样一段注释：

“利用高等数学研究单摆的运动就会看到，(1)式是个近似公式，由它算出的周期与精确值之间的差别伴随着偏角的增加而增加．当偏角θ为5°时两者相差0.01%，7°时两者相差0.1%，15°时两者相差0.5%，23°时两者相差1%．”

这里很自然地涉及两个问题：一个是理论上如何给出一个任意摆角的单摆振动周期的相对误差分布；另一个是在实验上，多大的振幅可以满足sinθ≈θ成立，使得小振幅单摆可以理论与实验相互自洽．

在开始讨论之前，我们先要纠正一下措辞，“单摆”这个名词的定义应当是被限定在小角度或小振幅情况下的摆动.当振幅很大时，摆动就不能再称之为单摆，于是我们采用“任意振幅摆”这个词来代表我们所研究的问题．

首先回答第二个问题，采取控制误差的方法，在实验测量中，认为sinθ是真实值，而θ是我们选取的近似值或者是“测量值”.计算其相对误差γ在γ0=0.1%的时候，所对应的角度值，有下列方程

可以得到数值解θ=4.44°，也就是说，在这个范围以内，都可以认为sinθ≈θ成立，即我们可以放心地使用线性微分方程来求解振动周期．但是，这样小的振幅，虽然在实验测量上的问题解决了，但是其“可视性”和“操作性”却相对一般.比如，作为演示实验使用的时候，距离稍远的观察者几乎就看不太清楚单摆的振动．为了解决这个问题，我们不妨非常大胆的将振幅增大，但是这需要严格控制误差，这就回到了第一个问题上.为此，我们需要计算任意振幅下摆的振动周期的相对误差．我们与很多文献不同，没有采用椭圆积分化为级数展开的方法[2]，而是采取从头计算的方法，直接给出精确表达式，直接进行数值积分，从而避免了一些不必要的步骤和误差．

2 模型和计算

如图1所示，其中θm为最大振幅，l是摆长，mg是振子所受的重力，对于任意的θ位置，由于只有重力做功，因此系统机械能守恒，选摆动平衡时所在位置为零势能面，有

mgl(1-cosθm)

(2)

可得

(3)

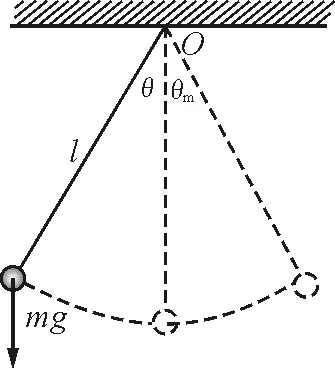
图1 单摆

对时间t积分，就可以得到小球从最低点第一次到达最高点的时间t0，再乘以4，就可得到整个运动的一个周期

(4)

这是一个广义含参积分．我们将

作为单摆周期的精确真实值，以此来计算大振幅情况下的系统误差γ(θm).

(5)

3 计算结果和讨论

式(5)即为摆角小于90°的任意振幅摆振动周期的相对误差的严格解析表达式.下面是数值计算的结果．我们给出以5°角为等差的任意振幅摆振动周期相对误差分布，如表1.

表1 任意振幅摆振动周期的相对误差

将表1给出的数据，绘制出如图2所示的系统相对误差γ(θm)与振幅θm的关系曲线.

图2 任意振幅摆振动周期的相对误差曲线

从图2可以看出，曲线有以下特点.

误差的增加整体上呈现一个非线性单调增长的趋势.在振幅趋近于零的时候，相对误差为零，在振幅达到90°的时候，相对误差为18%.

为何会出现上述结果？有一点很清楚，就是当振幅θm→0的时候，刚好满足第一部分所说的线性近似的条件，因而得出的周期就可以认为是真实值 ，误差γ→0．当振幅θm→90°时，相对误差达到了最大值．结合式(5)可知，曲线的单调增长说明了振动周期随着振幅θm的增长也呈现一个单调性的变化，从物理上讲，就是振幅越大，振动的周期越长．

此外，我们的计算结果在振幅θm超过30°之后，误差值均系统性地小于文献[3]中的结果.这其中的原因就在于当振幅θm较大时，对于sinθ的展开就不能只取到第二项的θ项，而是要继续考虑更高次幂的展开项.正是由于忽略了后面的高次项，因此必然会导致计算的误差偏大．

再从数值上看，当振幅θm=45°的时候，相对误差γ→ 4%，也就是说，如果一个固有周期为T0=10 s的小振幅单摆，当把它的振幅变到θm=45°的时候，周期变为

而0.4 s的差别，对于演示实验来说，是完全可以接受的．

4 结论

我们推导了任意振幅摆周期相对误差的解析表达式，利用从头算起的数值方法，计算了振幅介于0°到90°之间的单摆周期的相对误差．计算过程中没有采取近似，所以计算结果为准确的数值解．

参考文献

1 人民教育出版社课程教材研究所，物理课程教材开发中心.普通高中课程标准实验教科书(物理·选修3-4).北京：人民教育出版社，2007

2 喻利华，张月胜.单摆周期的数值计算.物理通报，2001(7)

3 吴云龙.对单摆周期测定值误差的诠释.中学物理教学参考，2004,33(6)