张家平

(华南理工大学 金融工程研究中心， 广东 广州 510006)

一、 前言

当前， 结构性产品市场迅猛发展， 并以其丰富投资品种、 扩大投资者选择、 按投资者的风险偏好“量身定制”投资产品(即具有不同优先等级的分券)、 转移信用风险等特征吸引了金融机构、 学术团体、 信用评级机构、 金融监管部门的广泛关注。2008年的金融危机只是使结构性产品市场的发展受到一时阻碍， 丝毫没有减少人们对结构性产品， 尤是CDO的关注和研究热情*专门汇集信用风险及其定价工作论文及专著的网站www.defaultrisk.com， 每周约有20篇的关于CDO定价和风险度量的新论文出现。。CDO是以债券、 贷款、 结构性产品、 甚至CDO产品构成的资产组合为担保而发行的， 按照一定优先等级进行支付权利金和承担损失的证券， 即分券(tranches)。因此， CDO 的价值主要由信用风险决定： CDO 的发起人定期向投资者支付权利金(也即CDO 的价值)， 以获得在违约发生时向投资者要求损失赔偿的权利。从量化的角度来看， 如何计算一段时期内信用资产组合整体违约损失的联合概率分布是对CDO 进行研究分析的基础。

对现有的模型和方法也有一些粗略的分类， 一是沿用单资产信用风险模型的分类， 将CDO定价模型划分为结构方法和简化方法。结构方法又称为企业价值方法、 默顿方法， 是由默顿基于期权理论[1]提出的违约风险模型[2]， 并由Hull等扩展到组合信用风险模型。[3]基于统计理论的简化方法， 又称为强度模型(intensity model)， 是Jarrow和Tunbull首次提出，[4]并由Dufie和Garlenu推广到组合水平对相依违约强度进行建模[5]； Schönbucher等人在更一般的copula框架下分析违约强度的相依结构。[6]二是最近提出的自下而上(bottom-up)和自上而下(top-down)方法。Kay Giesecke按这种分类方法对组合信用风险度量模型与方法进行了综述。[7]自下而上方法是从组合中各资产的违约强度通过加总推导出组合的违约强度， 而自上而下方法在无套利方式下直接对组合损失的随机动态机制进行建模。[8]

上述分类方法仅仅从建模出发点的不同对各种模型与方法进行粗略的分类， 并没有进一步分析各模型之间的内在联系以及模型改进的路线图， 不利于模型之间的比较与评价。再者， 分类方法的包容性存在一定局限， 比如第二种分类方法只是针对简化模型， 没有包括结构模型。因此， 我们迫切需要一个相对统一的框架， 能够把现有的大部分模型纳入这个框架， 找出人们对CDO产品定价和风险度量的认识和模型改进的内在逻辑进程， 便于模型的比较与评价。这是本文的主要目的。我们发现因子方法(factor approach)能够担当这个重任。因子方法以其包容性、 开放性将大部分现有模型包含在该框架中， 如图1所示。

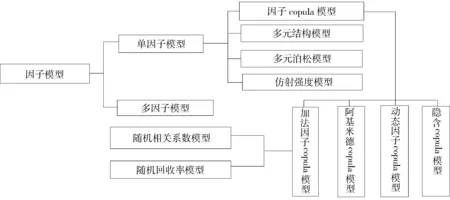
图1 因子方法框架图

从图1可以看出， 因子copula模型在刻画多元违约相关性中最具竞争力， 而且在此框架内很容易对模型进行拓展， 这一点与陈田和秦学志在对CDO定价模型综述中的结论是一致的。[9]

二、 因子copula模型及其拓展

因子copula模型是CDO定价和风险度量模型中最具活力的一个分支， 其最简单的形式， 单因子正态copula模型(one-factor Gauss copula model)已成为行业定价和风险度量的标准模型。同时， 因子copula模型具有良好的扩展性， 以不断改进对CDO显示价格的拟合效果。

在copula模型中， 违约时间的联合分布可写成一维的边缘分布和copula函数的组合， Copula模型能将相依结构(dependence structure)从联合分布中分离出来， 并与边缘分布无关等优良性质广泛运用于金融领域的多元分析。对copula方法的介绍及其在金融领域的运用可参考文章后面的参考文献第[10]和[11]。[10]52-125， [11]134-187

P(τ1≤t1, Lτn≤tn)=C(F1(t1), LFn(tn))

在这个框架下， 相依结构和边缘分布可以分开处理。通常， 边缘违约概率Fi(ti)可以从不同资产的信用违约互换权利金数据中推出， 或者根据信用评级机构的历史数据推出。因此， 他们可以看做是市场输入变量。由于相依结构是不可观测的， 只能通过选择不同的copula函数来刻画违约相依结构。这是因子copula定价模型最重要的一步， 当然也受到较多质疑。在信用风险领域， 因子copula方法首次由David Li[注]美籍华人Li被称为华尔街的精算天才， 其单因子正态copula模型被学界与期权定价的B-S公式相提并论， 并极大的推动了结构性产品市场的发展。引入，[12]由Schünbucher进一步发展[13]。

因子copula模型是一类特殊的copula模型， 其违约时间的相依结构服从因子框架。具体地说， 相依结构由一些隐含变量V1, …, Vn决定， 每个变量Vi表示成由共同风险因子Z和特殊风险因子εi构成的二元函数。

Vi=f(Z,εi),i=1, L,n

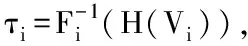
在一般copula框架下， 损失分布的计算要求n次连续积分。因子copula方法的好处在于， 由于因子的维度要要比N低得多， 从而大大简化了计算。

(一)加法因子copula(additive factor copula)模型

加法因子copula模型族在CDO分券定价中使用的最为广泛。在这类模型中， 函数f表示共同因子与特殊因子是相加的， 隐含变量V1, …, VN通过相依参数ρ联系起来。

(5)

根据前面的分析， 可得出条件违约概率Pt(Z)为：

(6)

在大多数运用中， Z和εi， i=1, …, N属于相同的分布， 以使通过卷积后得到封闭解。

这类模型中最受欢迎[注]最受欢迎不在于其准确性， 而在于计算简单， 易于处理。如同正态分布是在刻画资产收益率分布中最常采用的形式， 但我们知道现实资产收益率不服从正态分布。的模型形式就是所谓的因子正态copula模型， 即Z和εi， i=1, …, n为服从独立标准正态分布的随机变量， 从而隐含变量V1, …, VN亦为正态分布。Vasicek在信用风险领域首次引入这种设定方法[注]Vasicek没有直接采用copula函数这个名称， Li推出Vasicek模型与单因子正态copula模型是等价的。[14]， 而在统计学上称之为多元概率模型。尽管因子正态copula模型计算简单、 易于处理， 但它也有一些众所周知的缺陷： 不能完全拟合所有具有相同期限的标准CDO分券的市场报价， 存在相关系数微笑或相关系数倾斜等与模型设定不符的现象。

因子copula模型最大的优点在于容易扩展。[15]215-234从上面的模型设定可以看出， 第一， 改进风险因子的分布， 以反映金融资产收益率或风险因子的尖峰、 肥尾、 偏斜等特征。第二， 改进对风险因子相依结构的刻画， 错误的相依结构会导致对信用资产组合风险的严重低估。[16]通过选择合适的copula函数以逼近CDO参考资产组合真实的违约相依结构。一些学者采用具有肥尾特征的t-copula来研究信用风险问题，[17-21]t-copula的极限形式就是正态copula。同样， t-copula模型具有与正态copula模型类似的缺陷。

为解决相关系数微笑等正态copula模型的， 一些学者使用不同的分布来改进模型， 如双t分布[22]、 正态逆高斯分布(NIG)[23]、 双正态逆高斯分布[24]、 双方差Gamma分布[25]、 Lévy分布[26]259-278等， Wang等人讨论了其他具有肥尾分布的因子copula模型[27]263-286。

注意以上因子copula模型的分析都是假定回收率R和相关系数ρ是固定不变， 一个很自然的扩展就是将他们随机化。Andersen等人提出了RFL(random factor loading)模型和随机回收率模型[28]对该假定进一步放松， 将它们设定为随机的参数。

(二)阿基米德copula方法

阿基米德copula具有显性的表达式， 并用1到2个参数来度量相依关系等优点在金融领域、 尤其是在信用风险建模中获得广泛的运用。尤其是阿基米德copula本身是可交换的， 因此可采用因子模型的表达式， Marshall等人最早推出了阿基米德copula数的因子表达式[29]。 每一个阿基米德copula可以用逆拉普拉斯变换φ(.)和共同因子Z联系起来。在该方法下， 隐含变量表示为：

(14)

其中φ-1(.)表示拉普拉斯变换， εi， i=1, …, N为独立均匀分布随机变量。则随机向量(V1, …, VN)的联合分布就是φ-阿基米德copula。如果隐含变量是均匀分布的， 则条件违约概率可写成：

Pt(Z)=exp(-φ(F(t))Z)

(15)

在信用风险领域， 运用最广泛的阿基米德copula函数是Clayton、 Gumbel和Frank copula函数。文献[13]30-33主要讨论Clayton copula在CDO定价和风险度量中运用， 而文献[21], [34]进一步讨论Gumbel、 Frank等其它阿基米德copula函数在信用风险建模中的运用。

三、 多元分布因子模型

直接对多元分布建模， 而不借助copula函数对违约相依结构的描述， 是刻画违约相依结构的另一种重要方法。多元分布因子模型克服了因子copula模型中copula函数的选择问题。

(一)多元结构因子方法

多元结构因子模型是单资产信用风险定价中的首次通过时间模型(first passage time model)在多资产情况下的推广， 该模型假定违约时间是随机的， 为资产价值低于某个阀值的首次通过时间[35]。Arvanitis和Gregory 在多元正态分布背景下研究一篮子信用衍生产品定价时提出多元结构因子模型[36]98-153。Hull等人考察了单因子多元正态结构模型对CDO分券的定价。[3]

该模型假设， CDO参考组合具有n个企业(或债务人)， 资产价值的变化机制V1, …, Vn可简单的表示为n个相关的布朗运动。有：

(16)

其中， Z、 V1, …, Vn独立的标准维纳过程， 当过程变量Vi低于某个常数阀值c(不同的资产具有相同的阀值)。然后， 相应的违约时间表示为：

τi=inf{t≥0|Vi, t≤c},i=1, Ln

违约概率在已知共同因子过程Z的条件下是独立的。当违约事件的发生是可交换的时， 根据Finetti定理， 违约概率一定存在， 式(16)依然属于单因子框架。多元结构因子模型与因子copula模型相比较， 有以下不同： 一是在多元结构模型中违约概率不能以封闭解的形式写出， 因此只能采用模拟方法来估计违约损失分布。二是多元结构模型的共同因子Zt是随时间而变化的， 因此是一个动态模型； 而前面讨论的因子copula模型是静态的。三是两类模型对违约相依结构的刻画不同， 多元结构模型无须事先假定参考资产组合的违约相依结构， 直接根据估计出来的多元联合损失分布反映债务人的违约相依关系。

多元结构因子模型具有与首次到达时间模型相似的缺陷， 即只能采用Monte Carlo模拟的方法来进行估计， 计算非常耗时。对该类模型的拓展主要是对因子服从的随机过程的改进上， 以提高计算效率和拟合效果。

(二)多元泊松方法

CDO定价的多元泊松方法是将可靠性理论(reliability theory)， 又称为冲击模型， 移植到信用风险建模中。多元泊松模型认为违约时间是多元泊松过程发生第一次跳跃的时间， 当泊松过程Nti发生第一次跳跃， 将引发资产i的违约。违约事件的相依关系由引发一组资产以给定概率违约的系统事件或共同冲击之间的相依关系决定。在此框架下， 我们讨论最简单的情形， 即每次违约事件由特殊的死亡冲击(fatal shock, 即导致违约发生)或共同冲击引发， 共同冲击不一定是死亡冲击[注]注意特殊冲击与共冲击类似于因子模型中的特殊因子和共同因子。。则可导致资产i违约的泊松过程表示为：

(17)

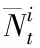
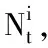
根据以上的分析， 可得违约概率为：

如同多元结构因子模型， 多元泊松方法依然属于单因子框架， 而且因子随时间改变， 所以该方法是动态方法， 并得到违约概率是离散的随机变量。

四、 仿射强度因子模型

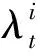
(18)

在仿射模型中， 违约时间的相依关系主要体现在违约强度的相依结构上。Duffie等人提出违约强度的因子表达式以刻画违约强度的相依结构。[8]

其中， α为非负参数， 反映了共同因子xt的重要性并控制违约强度的相依关系， x和xi是独立的， 并服从仿射跳跃扩散(AJD, affine jump diffusion)过程。选择AJD过程有以下两个优点： 一是违约强度λi也服从于仿射跳跃扩散过程， 从而可得到违约概率的解析表达式； 二是能得到灵活的违约强度的动态机制。缺陷是仿射强度模型不能所有期限的信用违约互换的报价， 参数校准过程比较复杂。

仿射强度模型对违约强度引入因子模型， 并且因子是随时间变化而改变的， 所以是动态模型。Gregory和Laurent较早采用仿射模型的因子表达式推出违约概率分布，[32]，[44-45]进一步推广了仿射强度模型， 增加参数选择的灵活性， 为参数校准和CDO分券定价发展更有效率的数值计算方法。Feldhutter运用信用违约互换和CDO分券价差的大量数据， 对仿射强度模型进行实证研究， 发现该模型与CDO分券的盯市(Marked-to-market)价差的匹配能力较好， 但不能抓住高级分券利差的变化。[46]

五、 结论

因子方法为大量的CDO定价和风险度量模型提供了一个统一的框架， 这对模型比较与选择、 抓住定价和风险度量模型的核心和未来发展趋势具有重要意义。通过上面的分析， CDO因子方法框架具有以下四个优点：

第一， 因子方法框架能容纳大部分主要的CDO定价和风险度量模型。近年来， 除因子copula模型外， 多元因子模型、 仿射强度因子模型也获得了较快发展， 为违约相依结构的度量提供了一种替代的方法。

第二， 因子方法是个开放的框架， 很容易进行拓展。可以看出， 有三条主线对CDO定价和风险度量模型进行拓展。一是改进因子分布或服从的随机过程、 共同因子的相依结构。二是对因子模型参数的随机化。三是多因子模型和动态因子模型的发展。现有的CDO定价和风险度量模型基本上都是按这三个方向展开的。

第三， 因子模型作为一种降维技术， 是解决违约相依结构维度问题的重要工具， 能极大的提高计算效率， 有些模型能得出违约分布的解析或半解析的结果。

第四， 随着多元分析理论与实践的发展， 一些新的降维技术不断被提出来。如独立成分析， 作为主成份分析和因子分析的进化版本， 在工程和信号系统领域获得广泛运用。我们有必要研究独立成分分析在组合资产定价和风险度量中的运用， 充分利用独立成分分析计算的准确性和高效性。

参考文献：

[1] Black F, Scholes M. The pricing of options and corporate liabilities [J]. Journal of Political Economy， 1973(3): 637-654.

[2] Merton R C. On the pricing of corporate debt: the risk structure of interest rates [J]. Journal of Finance， 1974(2): 449-470.

[3] Hull J, Predescu M, White A. The valuation of Correlation-dependent credit derivatives using a structural model [R]. New York: University of Toronto, 2005.

[4] Jarrow R A, Turnbull S M. Pricing derivatives on financial securities subject to credit risk [J]. Journal of Finance. 1995(5): 53-85.

[5] Duffie D, G arleanu N. Risk and the valuation of collateralized debt obligations [J]. Financial Analyst Journal, 2001(2): 51-59.

[6] Schonbucher P, Schubert D. Copula dependent default risk in intensity models [J]. Journal of Derivatives， 2001(3): 1-25.

[7] Giesecke K. Portfolio credit risk: top-down vs bottom-up [M]//Cont R. Frontiers in Quantitative Finance: Credit risk and Volatility modeling. Hoboken: John Wiley & Sons, 2009: 251-268.

[8] Schonbucher P J. Portfolio losses and the term structure of loss transition rates: a new methodology for the pricing of portfolio credit derivatives [J]. Journal of Computational Finance, 2006(1): 11-35.

[9] 陈田， 秦学志. 债务抵押债券(CDO)定价模型研究综述 [J]. 管理学报， 2008(4): 616-624.

[10] Nelsen R B. An Introduction to Copulas [M]. New York: Springer, 2006.

[11] Cherubini U, Luciano E, Vecchiato W. Copula Methods in Finance [M]. England: John Wiley & Sons Ltd, 2004.

[12] Li D. On default correlation: a copula approach [J]. Journal of Fixed Income， 2001(9): 43-54.

[13] Schonbucher P J, Schubert D. Copula dependent default risk in intensity models [J]. Journal of Derivatives, 2001(3): 1-25.

[14] Vasicek O. Loan portfolio value [J]. Risk， 2002(12): 160-162.

[15] Cowell F, Racheva B, Truck S. Recent advances in credit risk management [M]//Georg Bol, Rachev S T. Risk Assessment Decisions in Banking and Finance. Heidelberg: Springer, 2009:

[16] Embrechts P, Mcneil A, Straumann D. Correlation: Pitfalls and Alternatives [J]. Risk， 1999(12): 69-71.

[17] Andersen L, Sidenius J, Basu S. All your hedges in one basket [J]. Risk， 2003(11): 67-72.

[18] Frey R, Mcneil A. Dependent defaults in models of portfolio credit Risk [J]. Journal of Risk， 2003(1): 59-92.

[19] Mashal R, Naldi M, Zeevi A. Extreme events and multiname credit derivatives [M]//Gregory J. Credit Derivatives: The Definitive Guide. Landon:Risk Books, 2003: 313-338.

[20] Demarta S, Mcneil A. The t copula and related copulas [J]. International Statistical Review， 2005(1): 111-129.

[21] Schloegl L, Okane D. A note on the large homogeneous portfolio approximation with the student t copula [J]. Finance and Stochastics, 2005(4): 577-584.

[22] Hull J, White A. Valuation of a CDO and an nth to default CDS without Monte Carlo simulation [J]. Journal of Derivatives， 2004(2): 8-23.

[23] Guegan D, Houdain J. Collateralized debt obligations pricing and factor models: a new methodology using normal inverse Gaussian distributions [J]. Journal of Structured Finance, 2005(5): 12-35.

[24] Kalemanova A, Schmid B, Werner R. The normal inverse Gaussian distribution for synthetic CDO pricing [J]. Springer， 2007(3): 80-93.

[25] Moosbrucker T. Pricing CDOs with correlated variance gamma ditributions [J]. Journal of Quantitative finance, 2006(8): 1-34.

[26] Albrecher H, Ladoucette S, Schoutens W. A generic one-factor Levy model for pricing synthetic CDOs [M]//Rache V S. Advances in Mathematical Finance. Landon: Birkhäuser, 2007: 259-278.

[27] Wang D, Rachev S, Fabozzi F. Pricing Tranches of CDO and a CDS index: recent advances and future research [M]//Bol G, Rachev S, Wurth R. Risk Assessment: Decisions in Banking and Finance. Heidelberg: Physica-Verlag, 2009: 263-286.

[28] Andersen L, Sidenius J. Extensions to the Gaussian copula: random recovery and random factor loading [J]. Journal of Credit Risk， 2005(1): 29-70.

[29] Marshall A, Olkin I. Families of multivariate distributions [J]. Journal of American Statistical Association, 1988(7): 834-841.

[30] Laurent J, Gregory J. Basket default swaps, CDOs and factor copulas [J]. Journal of Risk， 2005(4): 103-122.

[31] Gregory J, Laurent J. I will survive [J]. Risk， 2003(6): 103-107.

[32] Madan D, Konikov M, Marinescu M. Credit and basket default swaps [R]. Bloomberg LP, 2004.

[33] Friend A, Rogge E. Correlation at first sight [J]. Economic Notes， 2005(2): 155-183.

[34] Rogger E, Schonbucher P. Modelling dynamic portfolio credit risk [R]. Imperial College, 2003.

[35] Black F, Cox J. Valuing corporate securities: some effects of bond indenture provisions [J]. Journal of Finance， 1976(1): 351-367.

[36] Marshall A, Olkin I. A multivariate exponential distribution [J]. Journal of the American Statistical Association, 1967(2): 30-44.

[37] Arvanitis A, Gregory J. Credit: the complete guide to pricing, hedging and risk management [M]. London: Risk Books, 2004.

[38] Lindskog F, Mcneil A. Common Poison shock models: applications to insurance and credit risk modeling [J]. ASTIN Bulletin， 2003(2): 209-238.

[39] Duffie D, Singleton K. Simulating correlated defaults [J]. Journal of Financial Risk, 1999(4): 23-41.

[40] Wong D. Copula from the limit of multivariate binary model [J]. Journal of American Statistical Association, 2000(4): 35-67.

[41] Giesecke K. A simple exponential model for dependent defaults [J]. Journal of Fixed Income, 2003(12): 74-83.

[42] Brigo D, Pallavicini A, Torresetti. CDO calibration with the dynamic generalized Poisson loss model [J]. Risk， 2007(5): 70-75.

[43] Brigo D, Pallavicini A, Torresetti R. Cluster-based extension of the generalized Poisson loss dynamics and consistency with single names [J]. Internatonal Journal of Theoretical and Applied Finance， 2007(4): 607-631.

[44] Mortensen A. Semi-analytical valuation of basket credit derivatives in intensity-based models [J]. Journal of Derivatives， 2006(4): 8-26.

[45] Eckner A. Computational techniques for basic affine models of portfolio credit risk [J]. Journal of Risk, 2007(6): 1-43.

[46] Feldhutter P. An empirical investigation of an intensity-based model for pricing CDO tranches [J]. Journal of Empirical Finance, 2007(3): 1-25.