凌蕾花

(镇江市高等专科学校人事处,江苏镇江 212003)

一致凸 Banach空间中非扩张非自身映射的弱收敛定理

凌蕾花

(镇江市高等专科学校人事处,江苏镇江 212003)

在具有 Opial条件或 Frechet可微的一致凸 Banach空间中,对非扩张非自身映射引入一类新的带误差的Ishikawa型迭代序列,并研究其逼近公共不动点问题。

非扩张非自身映射;公共不动点;一致凸 Banach空间;Opial条件;Frechet可微

0 引 言

Safeer Hussain Khan和 Hafiz Fukhar-ud-din[1]在一致凸 Banach空间中研究了两个非扩张自身映射下带误差的一类迭代序列的收敛性。Naseer Shahzad[2]在实一致凸Banach空间中研究了非扩张非自身映射的逼近不动点问题。本文将在一致凸Banach空间中对非扩张非自身映射引入一类新的带误差的迭代序列并研究其逼近公共不动点问题,主要结果如下:

定理 1设 E是实一致凸 Banach空间,K是 E的非空有界闭凸子集,P:E→K是保核收缩,T1,T2,T3:K→E是非扩张非自身映射,且 F(T1)∩F(T2)∩F(T3)≠∅,这里 F(T)表示 T的不动点集。定义 K中迭代序列 {xn}为

若 E满足下列条件之一:1)E具有 Opial条件;2)E具有 Frechet可微,则迭代序列 (1)弱收敛到 T1,T2,T3的某公共不动点。

1 引 理

引理 1对任何 f∈F(T1)∩F(T2)∩F(T3),极限存在。

证明因为 K有界,故存在 M ＞0,M′＞0,M″＞0,使得‖xn-un‖≤M,‖xn-vn‖≤M′,‖xn-wn‖≤M″,∀n∈N,从而对任何 f∈F(T1)∩F(T2)∩F(T3),

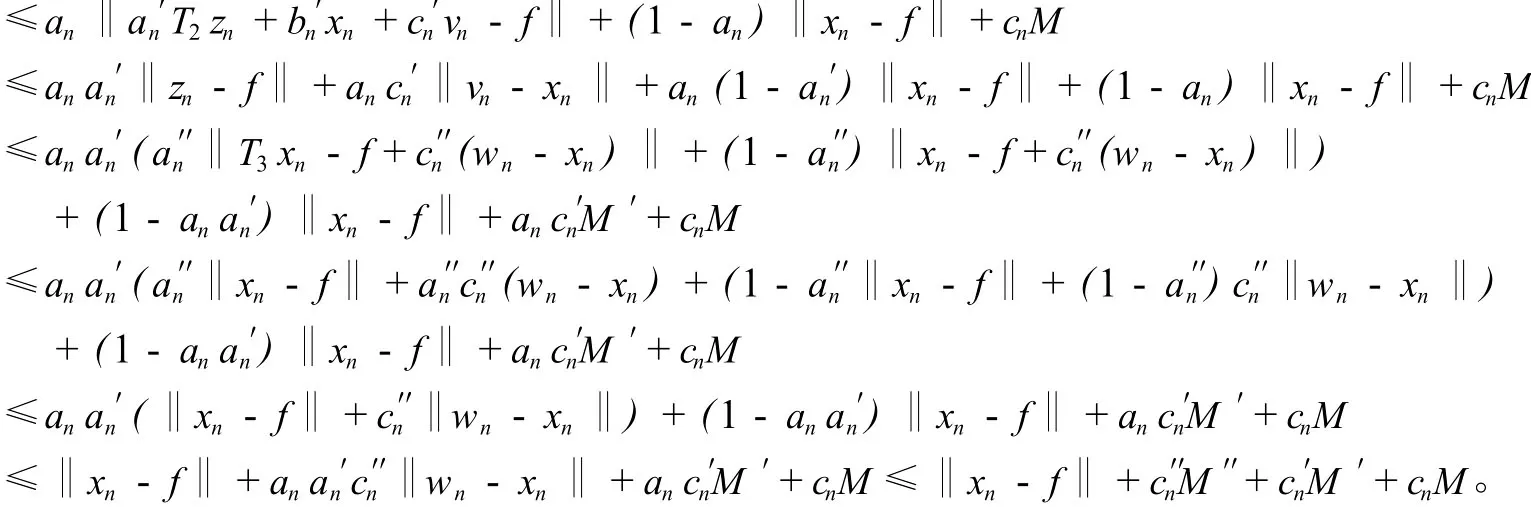
类似于引理 1的证明,我们可证

引理 2

令Wnx=P(anT1P(a′nT2P(a″nT3x+b″nx+c″nwn)+b′nx+c′nvn)+bnx+cnun),则

定义 Un,m=Wn+m-1Wn+m-2…Wn,则 Un,mx=xn+m。且对任意的 x,y∈K,有

引理 3设

由归纳法可得

引理 4设 0＜λ＜1,f,g∈F(T1)∩F(T2)∩F(T3),则‖存在。

证明由定理 1[3]得

两边先对 m取上极限,得

引理 5若f,g是{xn}的弱极限点,且,对任意的ε＞0,∃N0∈N,当 n＞N0时,有 ‖λxn+(1-λ)f-g‖≤h(λ)+ε,则

又 f为{xn}的弱极限点,则 ∃ ni,ni＞N0时,使得

证明记ε)‖f-g‖,‖f-g‖≤h(λ)+ε。又因为ε＞0是任意的,则 ‖f-g‖≤h(λ)。

3 定理 1的证明

证明我们仅需说明ωω{xn}为单点集。设 f,g都为{xn}的弱极限点,下证 f=g。

首先由引理 1,引理 2和半闭原理[4-5]知,f,g∈F(T1)∩F(T2)∩F(T3)。

1)若E是具Opial条件的一致凸 Banach空间,若 f≠g,则存在{ni},{nj},使得,由引理 1及 Opial条件可得类似可得矛盾,从而 f=g。故{xn}弱收敛到 T1,T2,T3的公共不动点。

2)若 E是具 Frechet可微范数的一致凸 Banach空间,则‖f-g‖=〈xn-f,J(f-g)〉关于 n≥1一致成立。由引理 4与引理 5知,从而对任意的ε＞0,存在N′0,当n＞N′0时,有〈xn-f,J(f-g)〉＞-ε,又g∈ωω{xn},∃n′i＞N′0,使得,则〈xn′i-f,J(f-g)〉＞ -ε,两边对 i取极限,有〈g-f,J(f-g)〉≥ -ε,即 ‖f-g‖2≤ε,由ε的任意性可知 f=g。

注:1)当cn=c′n=c″n=0,T1=T2=T3=T时,定理就是文献[2]中的定理3.5。2)当a″n=b″n=c″n=0,T1,T2为 K→K的非扩张映射时,定理 1就是文献[1]中的定理 1。

定理 1将文献[1]中的相应结果推广到非自身映射三重迭代情形,将文献[2]中的相应结果推广到带误差的三重迭代情形,同时减弱了文献[1,2,4,6,7,8]中的紧性或全连续条件。

[1]KHAN S H,FUKHAR-UD-D IN H.Weak and strong convergence of a scheme with error for two nonexpansive mappings[J].NonlinerAnalysis,2005(61):1295-1301.

[2]SHAHZAD N.Approx imating fixed points of non-self nonexpansive mappings in Banach spaces[J].Nonliner Analysis,2005(61):1031-1039.

[3]BRUCK R E.On the convex approximation property and the asymptotic behavior of nonlinear contractions inBanach spaces[J].Israel J.Math.,1981(38):304-314.

[4]TAN K K,XU H K.Approximating fixed points of nonexpansive mappings by the Ishikawa iteration process[J].Math.Anal.Appl.,1993(178):301-308.

[5]GRORN I CH I J.Week convergence theorems for asymptotically nonexpansive mappings in unifor mly convex Banach space[J].CommentMath Univ Carolin,1989,30(1):249-252.

[6]L I G,K IM J K.Nonlinear ergodic theorem for a general curve defined on general semigroups[J].Nonlinear.Anal.,2003(55):1-14.

[7]TAKAHASH IW,K IM G E.Approximating fixed points of nonexpansive mappings in Banach spaces[J].Math.Japonica,1998(48):1-9.

[8]ZENGL C.Ishikawa iteration process for approximating fixed points of nonexoansive mapping[J].Journal ofMathematical Reseach&Exposition,2003,23(1):33-39.

〔责任编辑:卢 蕊〕

Abstract:This paper introduces a new Ishikawa iteration processwith errors for non-expansive and non-self mappings in a uniformly convexBanach space,which satisfiesOpial's condition or has a Frechet differentiable nor m and makes research on how to approach the common fixed point.

Key words:non-expansive and non-selfmappings;common fixed point;uniformly convex Banach space;Opial's condition;Frechet differentiable nor m

Weak convergence theorem for non-expansive and non-self mapp ings in un iform ly convex Banach spaces

L INGLei-hua
(PersonnelDepartment,Zhenjiang College,Zhenjiang 212003,China)

O177.91

A

1008-8148(2010)04-0033-04

2010-07-02

凌蕾花 (1979—),女,江苏镇江人,讲师,硕士,主要从事泛函分析研究。