摘  要：单元教学是落实数学核心素养培养的一种重要方式. 但在实际教学中，部分教师对怎样进行单元教学分析、怎样理解教材的编排方式、怎样挖掘教材习题的价值仍然存在困惑. 从数学史的视角审视以上问题，能促进教师更好地理解和把握单元教学的联系性和整体性.

关键词：圆锥曲线；数学史；单元教学

数学单元教学是指在整体观念的引导下，以培养学生数学核心素养为目标，对教学内容进行整合优化，将处理后的教学内容作为一个相对独立的教学单元，以便凸显教学内容的主要线索及知识之间的逻辑关系. 单元教学有利于借助大框架进行高观点统领、思想性驾驭、结构化关联，能有效规避课时教学整体感不强、学习碎片化的问题，有利于促进知识和方法的迁移.

然而，在实际教学中，也有部分教师不清楚怎样进行单元教学分析，不了解如何处理单元与课时的关系，不明确在单元教学中怎样挖掘教材习题的价值. 这部分教师仍采用单个课时推进的方式进行课堂教学，对每节课涉及的知识做面面俱到的讲解，其所谓单元教学只是在学完一单元内容后进行简单总结，学生在课堂中所学的知识依然是碎片化的.

本文以人教A版《普通高中教科书·数学》选择性必修第一册（以下统称“新版教材”）中的“圆锥曲线的方程”单元为例，从知识内容的联系性和研究方法的整体性角度对教材进行分析. 再以此为基础，从数学史的视角尝试解决一些单元内容重构时的困惑.

一、“圆锥曲线的方程”单元的教材内容分析

“圆锥曲线的方程”的单元设置以三种圆锥曲线的概念和相关特征的学习为主线，三种圆锥曲线在知识内容上有一定的逻辑关系，研究方式有较强的关联性.

从几何角度来看，圆锥曲线是用平面截圆锥所得的截线，故三种曲线之间具有天然的内在联系，借助离心率可以得到它们的统一定义. 此外，三种圆锥曲线的“个性特征”也很明显，新版教材以三种圆锥曲线的“个性特征”为明线定义三种圆锥曲线. 同时，以具体实例结合延伸性材料的方式渗透“统一定义”.

從代数角度来看，用代数方法研究圆锥曲线具有一般模式：呈现背景—归纳概念—标准方程—研究几何性质—具体应用. 每个环节也有一定的程序性，特别是求标准方程的步骤，将用坐标法处理几何问题的优势体现得淋漓尽致，也使学生深刻认识到了数和形的辩证统一，这是本单元学习的一条暗线.

新版教材对本单元内容的呈现是“总—分—总”的编排方式. 首先，通过梅内克缪斯平面截直圆锥模型总体建构椭圆、双曲线、抛物线的概念，引出大单元的学习内容. 其次，分三个子单元进行学习，每个子单元的研究方法和操作过程是相似的. 换言之，通过椭圆的学习就能弄清楚圆锥曲线的研究套路，也就是说，椭圆的学习是本单元的重点内容. 最后，在知识学习的基础上进行单元总结回顾，形成圆锥曲线学习研究的大框架.

二、圆锥曲线（椭圆）定义的追溯

1. 教学内容重构时的困惑

我们知道，圆锥曲线至少有三种定义方式，第一种是截线定义，第二种是轨迹定义，第三种是焦点准线定义. 那么，这三种定义之间有什么关联？旦德林双球模型的意义何在？此外，为什么要把椭圆、双曲线、抛物线称为“圆锥曲线”？现实生活中看到的椭圆形象是否与“两钉一线”画出的椭圆一致？

在教学中要怎样解决以上类似的困惑呢？或许，追溯圆锥曲线（椭圆）的定义可以给我们一些启示.

2. 圆锥曲线定义的历史演进

第一阶段：圆锥截线定义.

公元前4世纪，圆锥曲线登上了数学舞台，古希腊数学家梅内克缪斯用一个与母线垂直的平面去截顶角分别是锐角、直角和钝角的直圆锥，得到了椭圆、抛物线和双曲线（如图1），此时圆锥曲线没有焦点的概念.

第二阶段：椭圆性质的研究和第二定义的出现.

梅内克缪斯之后，阿波罗尼奥斯（Apollonius）使用平面截对顶斜圆锥来表示圆锥曲线，人教A版《普通高中课程标准实验教科书·数学选修2—1》（以下统称“旧版教材”）第二章的章前图呈现了截线情形（如图2），只不过章前图中的圆锥是直圆锥. 对于缺乏代数工具的古希腊时期而言，研究圆锥曲线绝非易事. 以椭圆为例，阿波罗尼奥斯使用纯几何方法倾尽全力才获得椭圆的焦半径性质，即椭圆上任意一点的两条焦半径之和等于长轴的长.

公元4世纪，帕普斯（Pappus）用几何方法证明了“平面上，到一个定点和一条定直线的距离之比等于常数的动点轨迹为圆锥曲线，常数小于、等于和大于1时，轨迹分别是椭圆、抛物线和双曲线”. 这便是我们熟知的焦点准线性质，也被称为椭圆的第二定义.

第三阶段：从椭圆画法到轨迹定义.

因设计圣索菲亚大教堂而享誉世界的拜占庭数学家安提缪斯（Anthemius）依据阿波罗尼奥斯发现的椭圆焦半径性质得出了我们熟悉的“两钉一线”椭圆作图法，又称“园艺师画法”. 17世纪，法国数学家和天文学家拉希尔在《圆锥曲线新基础》中给出了椭圆的焦半径定义；法国数学家洛必达根据“园艺师画法”，以及拉希尔的新定义推导出了椭圆的方程.

第四阶段：截线定义与轨迹定义的统一.

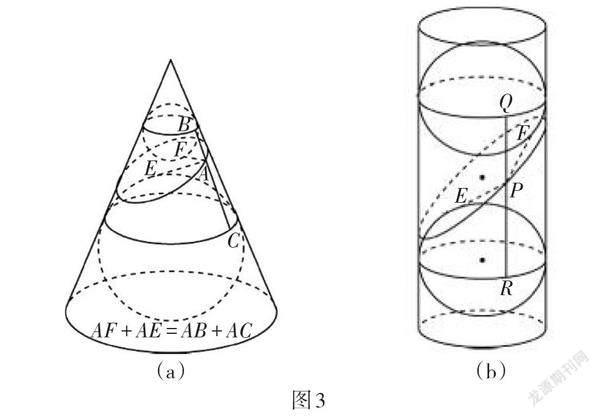
1822年，比利时数学家旦德林首次借助圆锥的内切球，通过圆锥直接推导出了椭圆的焦半径性质，从而直观证明了椭圆的轨迹定义与截线定义的一致性，也就是旧版教材第42页“为什么截口曲线是椭圆”所呈现的内容（如图3）.

笛卡儿的《几何学》激发了人们对圆锥曲线的研究兴趣，人们开始关注圆锥曲线的绘制. 17世纪，荷兰勤于动手的数学家舒腾（F.van Schooten）设计了多种不同的圆锥曲线规（如图4），这些圆锥曲线规通过命题人的改编融于试题呈现在学生面前. 例如，2015年高考湖北卷理科第21题就与图4（a）有关. 此外，这些圆锥曲线规也为教学提供了丰富的素材. 例如，教师在教学时可以利用信息技术展示圆锥曲线规的操作方法，以提升学生的直观想象素养；也可以让学生从圆锥曲线规作图的角度对三种圆锥给出新定义，或者用解析法求出所绘曲线的标准方程.

三、对教材单元内容编排的一些思考

历史相似性原理是指困扰世界的东西也会困扰儿童，世界克服其困难的方式提示教师儿童在其发展过程中会以类似的方式克服类似的困难. 用历史相似性原理考虑教材内容的编排，可以让我们更好地理解编写者的意图（如图5）.

由圆锥曲线（椭圆）历史的追溯可知，平面截圆锥得曲线的截线定义是最原始的定义，其他的定义均为由这个原始定义推导出的性质，并且截线定义也符合学生的直观认知. 但是由于三种截线都没有明显的几何特征，故要在此基础上得出圆锥曲线的标准方程对推导者的几何能力要求较高，且推理过程比较复杂，超出了大多数学生的接受范围，显然不合适. 轨迹定义可以与圆的定义相衔接，容易作图，进而得出“平面内与两个定点[F1，F2]的距离的和等于常数（大于[F1F2]）的点的轨迹叫做椭圆”的定义，再由“距离的和等于常数”联想到“距离的差等于常数”也是很自然的. 因此，在教材中，“椭圆及其标准方程”一节先直接呈现椭圆的具体画法，再给出椭圆的定义，符合先有“两钉一线”画法再产生轨迹定义的历史顺序.

但是这样选择也存在问题.

一是与抛物线的定义无法衔接. 对于这个问题，新版教材的处理方式是以焦点准线定义为补充，在椭圆、双曲线的内容上设置铺垫. 例如，椭圆部分主要是第113页例6“动点[Mx，y]与定点[F4，0]的距离和点[M]到定直线[l]：[x=2/54]的距离的比是常数[4/5]，求动点[M]的轨迹”；第115页习题3.1第8题“点[M]与定点[F2，0]的距离和它到定直线[x=8]的距离的比是1∶2，求点[M]的轨迹方程，并说明轨迹是什么图形”；第116页“用信息技术探究点的轨迹：椭圆”. 双曲线部分主要是第125页例5“动点[Mx，y]与定点[F4，0]的距离和它到定直线[l]：[x=9/4]的距离的比是常数[43，] 求动点[M]的轨迹”；第127页习题3.2第10题“设动点[M]与定点[Fc，0 c>0]的距离和点[M]到定直线[l]：[x=a2/c]的距离的比是[c/a a

二是有调查发现，学生对此心存疑惑：椭圆的画法是怎么想到的？定点为什么是两个，而不是三个？为什么会与距离有关，而不是其他呢？……对于类似问题，新版教材进行了一些相应处理：（1）通过第142页的“文献阅读与数学写作”栏目引导学生自行查阅与解析几何的形成与发展有关的文献，写一篇数学小论文，从而使问题得到部分解决；（2）将只需要简单的代数运算就可以得到的性质设置为例题和习题. 例如，例题和习题中设计了从“角度”间的关系导出的性质. 第108页例3“如图6，设[A，B]两点的坐标分别为[-5，0， 5，0.] 直线[AM，BM]相交于点[M，] 且它们的斜率之积是[-4/9]，求点[M]的轨迹方程”；第121页探究“如图7，设[A，B]两点的坐标分别为[-5，0，][5，0.] 直线[AM，BM]相交于点[M，] 且它们的斜率之积是[4/9，] 试求点[M]的轨迹方程，并由点[M]的轨迹方程判断轨迹的形状，与上述例3比较，你有什么发现”；第126页练习1“已知[A，B]两点的坐标分别是[-6，0，][6，0，] 直线[AM，BM]相交于点[M，] 且它们的斜率之积是[2/9.] 求点[M]的轨迹方程，并判断轨迹的形状”.

上述问题可以看作“直径所对的圆周角是直角”的改造，具有拓展性，为课堂教学留下了发挥的空间.

四、怎样挖掘教材习题的价值

作为教材内容的重要组成部分，习题在促进学生知识的巩固、能力的提升、思维的发展等方面有着不可代替的作用，从数学史的角度对教材习题进行拓展和引申，能促使教师更好地理解试题编制的意图和潜在的教育教学价值. 限于篇幅，下文仅以一个具体实例谈谈如何挖掘教材习题的价值.

新版教材第115页的综合运用题2是一道与多个圆有关的轨迹问题，具体如下.

题目  一动圆与圆[x2+y2+6x+5=0]外切，同时与圆[x2+y2-6x-91=0]内切，求动圆圆心的轨迹方程，并说明它是什么曲线.

学生通过解决上述问题，能够掌握圆与三种圆锥曲线的转化关系，在加深理解基本概念的同时，有利于构建本单元与上一单元“直线与圆的方程”内容之间的联系，体现所学知识的统一性，是发展学生思维能力的良好素材. 此外，其作为重要的命题背景出现在了高考试卷中，如2011年高考广东卷理科第19题、2013年新课程全国Ⅰ卷理科第20题等.

在传统数学文化中，诸如此类的问题常被称为“容圆问题”，指求一个圆（或几个互切的圆）与给定的直线（或圆弧线）相切，称所求的圆为“容圆”.

晚清时期，数学家黄宗宪、蒋维钟、周达等人都对“容圆问题”进行过研究，其中以周达的研究较为系统. 周达在其专著《平圆互容新义》中将动圆与两定圆（或直线与圆）的相切方式概括为下列三种情形.

情形1：如图8，半径不相等的两个圆相交，或内切，或内含时，动圆若与其中一个圆内切，与另一个外切，则其圆心的轨迹是椭圆.

情形2：如图9，半径不相等的两圆相离，或外切，或相交，动圆若与两定圆都相切（分外切和内切两种情形），则其圆心轨迹是双曲线.

情形3：如图10，一定直线与一定圆相离，或相切，或相交，若动圆与定圆及定直线都相切，则其圆心轨迹是抛物线.

周达对每种情形都给出了相应的证明，但可以看出总结得还不够完善，一些细节上存在着失误.

考虑到问题的重要性，许多一线教师进行了深入、细致地分析：有的从用几何画板软件演示的角度进行思考；有的对圆心轨迹可能出现的情形进行讨论，但讨论的情形不太完整，也存在一些值得商榷的细节问题.

在教学中，解决这类问题能使学生进一步感受分类讨论和数形结合的思想. 此外，借鉴历史上数学家对“容圆问题”的研究经验，教师能够对课堂上可能出现的障碍或困难进行预判，从而更加理性、从容地处理学生的错误与不足.

五、结束语

数学史的应用为单元教学分析开辟了一条新的途径，为教师提供了理解教材、改进教学的工具，对教师如何处理教材习题、获取习题背后的价值给予了参考，在丰富教学素材的同时，使得教师更加明晰教材编写者的意图，加深了对单元教学整体性的理解，从而使学生数学核心素养的培养在课堂上得到落实.

参考文献：

［1］徐章韬，汪晓勤. 从机械圆锥曲线规到电子圆锥曲线规［J］. 数学通报，2016，55（3）：54-57，59.

［2］万兵，李景财.“HPM”视角下的课堂教学实践与反思［J］. 数学教学通讯（上旬），2019（12）：7-9.

［3］高红成. 晚清数学家对容圆问题圆心轨迹的理论探讨［J］. 内蒙古师范大学学报（自然科学汉文版），2015，44（6）：839-845.

［4］李迪. 中國科学技术史论文集（第一集）［M］. 呼和浩特：内蒙古教育出版社，1991.

［5］张青松. 容圆圆心轨迹问题的教学启示［J］. 课程教材教学研究（中教研究），2019（5 / 6）：39-41.

作者简介：张青松（1984— ），男，中学一级教师，主要从事高中数学教学和高考命题研究.