乔慧娟，原 军

(太原科技大学 应用科学学院，太原 030024)

由数千个处理器组成的多处理器系统能够提高计算的能力，但如果多处理器系统中某个处理器出现故障，就可能造成整个互连网络的瘫痪。发现故障处理器，并用无故障处理器将其替换，是保证多处理器系统运行的安全性和可靠性的重要手段。因此，故障诊断度，即系统能诊断出的故障处理器的最大数量，成为评估多处理器系统可靠性的一个重要指标。

1967年，Preparata，Metze和Chien[1]建立了一个系统级诊断模型，称为PMC模型。它通过系统本身自动测试处理器，这大大提高了系统故障诊断的效率。之后研究人员还建立了许多系统级诊断模型，例如BGM模型[2]、比较模型[3]。本文考虑Preparata，Metzem和Chien提出的PMC模型。

因为经典的诊断度对顶点没有任何限制，所以当连接到某个顶点的所有邻点同时出现故障时，系统将没有办法判断该顶点的状态。因此，经典的诊断度总小于系统的最小度。为了更好地反映实际系统中的故障模式，2005年，Lai等人[4]提出了条件诊断度，它假设在一个系统当中任意顶点的所有邻点都不会同时出现故障。条件诊断度可以更好地衡量系统的可诊断能力。

2012年，Peng等人[5]提出了一个更一般的限制条件，要求每个无故障顶点连接大于等于g个无故障邻点。在此条件下，系统的诊断度称为g-好邻条件诊断度。之后系统的g-好邻条件诊断度得到了广泛的研究，譬如，Wang等人[6]研究了MM*模型下超立方体的g-好邻条件诊断度；Yuan等人[7]研究了PMC模型下和MM*模型下k元n方体的g-好邻条件诊断度；Li等人[8]研究了PMC模型下和MM*模型下星图的g-好邻条件诊断度。

2007年，Hsu等人[9]发现之前的大多数文献都在研究整个系统上的诊断度，而忽略了系统中的局部信息。于是，他们提出了局部诊断度的概念并研究了PMC模型下星图的局部诊断度。2019年，Yin和Liang[10]提出了g-好邻局部诊断度的概念，并研究了PMC模型下超立方体的g-好邻局部诊断度。

星图是一类重要的多处理器系统网络拓扑，它具有结点度低，对称性好，直径小和高度的容错性。因其良好的拓扑性质被作为互连网络拓扑应用于许多多处理器计算机系统之中[11-12]。本文讨论并得到PMC模型下星图Sn的每个结点的g-好邻局部诊断度。再结合g-好邻局部诊断度和g-好邻诊断度的关系，可以推出星图在PMC模型下的g-好邻诊断度。

1 基本概念及符号说明

多处理器系统通常建模为一个无向简单图G(V(G)，E(G))，其中顶点代表处理器，边代表处理器之间的通信链接。文中常省略字母G，例如分别用V，E代替V(G)，E(G).在无向图G(V，E)中，(u，v)=e∈E表示顶点u和v之间的边，u和v是e的端点且彼此相邻。对于一个顶点u∈V，符号NG(u)表示u的所有邻点的集合。图G中顶点u的度用dG(u)或d(u)表示，δ(G)表示G的最小度。若对所有的顶点v∈V，有d(v)=k，则称图G是k-正则的。令F⊆V，定义NG(F)=(∪v∈FNG(v))F为G中顶点集F的邻集。GF是G的一个子图，它是通过删掉F中的所有顶点和与F中顶点相关联的边而得到的。在图G中，如果GF不连通，则称F为G的顶点割。使G只剩下一个顶点或不连通，需要删除的最小顶点数称为G的连通度，记作κ(G).如果每个顶点u∈VF在VF中至少有g个邻点，则子集F⊆V称为G的Rg-顶点集，也称g-好邻条件集。若顶点子集F是连通图G的Rg-顶点集且GF不连通，则称F是G的Rg-顶点割。G的Rg-顶点连通度，用κg(G)表示，是G的最小Rg-顶点割的顶点数。定义F1，F2⊆V的对称差F1ΔF2=(F1F2)∪(F2F1).

在PMC模型中，系统中两个直接相连的顶点可以互相发送测试消息。对于任意两个相连的顶点u和v，有序对(u，v)表示顶点u在其邻点v上执行的测试。测试任务T是每个相邻顶点对的测试的集合。可以将其建模为有向图T=(V，L)，其中V是G的顶点集，L={u→v|u，v∈V(G)，(u，v)∈E(G)}.测试任务T的所有测试结果的集合称为校正子，从形式上说，它是一个函数σ:L→{0，1}.σ(F)表示故障顶点集F可能产生的所有校正子的集合。假设F1和F2是V中两个不同的集合，如果σ(F1)∩σ(F2)=∅，则F1和F2是可区分的且(F1，F2)是可区分对，否则，F1和F2是不可区分的且(F1，F2)是不可区分对。

下面给出了PMC模型下两个故障集是可区分的充要条件。

定理1[13]对于G中任意一对相异的顶点子集F1和F2，(F1，F2)是一个可区分对当且仅当存在两个顶点u∈F1ΔF2，v∈V(F1∪F2)使得(u，v)∈E.(见图1).

图1 PMC模型下的可区分对(F1，F2)Fig.1 A distinguishable pair(F1，F2)under the PMC model

2005年，Lai等人提出了条件诊断度的定义。G的条件诊断度tc(G)=max{t|G是条件t-可诊断的}。

2012年，Peng等人扩展了条件诊断度的概念，提出了g-好邻条件诊断度tg(G)=max{t|G是g-好邻条件t-可诊断的}。

引理1如果系统G中任意一对满足|F1|≤t，|F2|≤t的条件故障集F1，F2是可区分的，则系统G是条件t-可诊断的。

引理2如果系统G中任意两个满足|F1|≤t，|F2|≤t的g-好邻条件故障集F1，F2是可区分的，则系统G是g-好邻条件t-可诊断的。

2007年，Hsu等人通过研究系统的局部信息，提出了局部诊断度。系统G在顶点u处的局部诊断度tl(u)=max{t|G在顶点u处是局部t-可诊断的}。

引理3令G是一个图并且u是G中的一个顶点，顶点u是局部t-可诊断的当且仅当对于任意一对满足|F1|≤t，|F2|≤t，u∈F1ΔF2的不同的条件故障集F1，F2⊆V是可区分的。

定义1在系统G中，如果tl(u)=d(u)，则称顶点u∈V是强局部可诊断的。

定义2如果G的每个顶点都是强局部可诊断的，则系统G是强局部可诊断的。

2019年，Yin和Liang提出了g-好邻局部诊断度并得到了下面的一些结论。

引理4图G在顶点u∈V处是g-好邻局部t-可诊断的当且仅当对于任何一对满足|F1|≤t，|F2|≤t，u∈F1ΔF2的不同的g-好邻条件故障集F1，F2⊆V，(F1，F2)是一个可区分对。

引理5[10]系统G在顶点u处的g-好邻局部诊断度tgl(u)=max{t|G在顶点u处是g-好邻局部t-可诊断的}。

引理6图G是g-好邻条件t-可诊断的当且仅当G的每个顶点都是g-好邻局部t-可诊断的。

n维星图记为Sn，它的顶点集V(Sn)={u1u2…un|ui∈{1，2，…，n}并且ui≠uj对于i≠j}.两个顶点u和v是相邻的当且仅当u的标号可以通过将v的标号的第一个元素与第i个元素(2≤i≤n)互换得到，即若u=u1u2…ui-1uiui+1…un，v=uiu2…ui-1u1ui+1…un，则u和v相邻。Sn是由n!个顶点和(n-1)n!/2条边组成的，并且对于任意整数n≥3，Sn是n-1正则、点可迁、边可迁的偶图。图2给出了一个3维星图S3和4维星图S4.

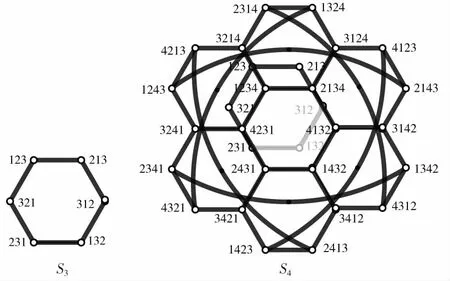
图2 3维星图和4维星图Fig.2 3D and 4D star graphs

2 PMC模型下星图的g-好邻局部诊断度

这个部分讨论PMC模型下星图的g-好邻局部诊断度，下面先给出一些相关的定理和引理：

定理2[14]当0≤g≤n-2时，Sn的Rg-顶点连通度κg(Sn)=(n-g-1)(g+1)!.

引理7当n≥3时，n维星图Sn是强局部可诊断的。

引理8设H是Sn的子图且δ(H)≥g，则|V(H)|≥(g+1)!

引理9令H是星图Sn的一个子图，顶点集V(H)={h1h2…hg+1(g+2)…n|1≤hi≤g+1，0≤g≤n-2，n≥4}，且令F1=NSn(H)，F2=F1∪V(H)，则|F1|=(n-g-1)(g+1)!，|F2|=(n-g)(g+1)!，并且F1，F2是g-好邻条件故障集。

定理3设整数0≤g≤n-2，n≥4，那么在PMC模型下n维星图Sn中任意一个顶点u∈V(Sn)，都有u的g-好邻局部诊断度tgl(u)≤(n-g)(g+1)!-1.

证明运用引理4证明tgl(u)≤(n-g)(g+1)!-1，即在Sn中有两个满足|F1|≤(n-g)(g+1)!，|F2|≤(n-g)(g+1)!

且u∈F1ΔF2的不同的g-好邻条件故障集F1，F2⊆V(Sn)，F1和F2是不可区分的。令H，F1和F2的定义如引理9(如图3所示)且由Sn的对称性，不妨设u=12…n.则u∈V(H)=F2F1=F1ΔF2.由引理9可知|F1|≤(n-g)(g+1)!，|F2|≤(n-g)(g+1)!，并且F1和F2是g-好邻条件故障集。注意到V(Sn)(F1∪F2)与F1ΔF2之间不存在边。由定理1，F1和F2是不可区分的。所以星图Sn在u∈F1ΔF2点处不是g-好邻局部(n-g)(g+1)!-可诊断的。

图3 F1，F2和H的关系图Fig.3 A diagram of F1，F2 and H

定理4设整数0≤g≤n-2，n≥4，那么在PMC模型下n维星图Sn中任意一个顶点u∈V(Sn)，都有u的g-好邻局部诊断度tgl(u)≥(n-g)(g+1)!-1.

证明首先，考虑g=0的情况。此时，对Sn的故障集没有条件限制。因此，对于Sn中的任意顶点u，Sn在u处的g-好邻局部诊断度等于Sn在u处的局部诊断度。因为n≥4，所以由引理7和定义2可以推断出V(Sn)的每个顶点都是强局部可诊断的。由于Sn是(n-1)-正则的，根据定义1可以得出，对于任意顶点u∈V(Sn)，Sn在u处的局部诊断度等于顶点u的度，即tl(u)=dSn(u)=n-1.当g=0时，(n-g)(g+1)!-1=n-1.因此tgl(u)=tl(u)=n-1≥(n-g)(g+1)!-1，结论成立。

接下来，考虑1≤g≤n-2的情况。由引理4，只需证明对于任意两个满足|F1|≤(n-g)(g+1)!-1，|F2|≤(n-g)(g+1)!-1并且u∈F1ΔF2的不同的g-好邻条件故障集F1和F2，(F1，F2)是可区分对。反之，假设存在顶点u和两个不同的g-好邻条件故障集F1和F2，其中|F1|≤(n-g)(g+1)!-1，|F2|≤(n-g)(g+1)!-1，使得F1ΔF2包含顶点u，但(F1，F2)是不可区分对。讨论以下两种情况。

情况1F2F1=∅或F1F2=∅.

不失一般性，假设F2F1=∅且u∈F1F2≠∅.则V(Sn)(F1∪F2)=V(Sn)F1且F1ΔF2=F1F2.由于F1和F2是不可区分的，故由定理1可知，要么V(Sn)=F1，要么V(Sn)≠F1且V(Sn)F1与F1F2之间不存在边。

子情况1.1V(Sn)=F1

由于1≤g≤n-2，n≥4且|F1|≤(n-g)(g+1)!-1，故n!=|V(Sn)|=|F1|≤(n-g)(g+1)!-1≤(n-(n-2))(n-2+1)!-1=2(n-1)!-1

子情况1.2V(Sn)≠F1

此时，V(Sn)(F1∪F2)和F1ΔF2之间没有边。由V(Sn)≠F1可知，F1∩F2是Sn的一个顶点割。因为F1和F2是g-好邻条件故障集，所以F1∩F2也是g-好邻条件故障集，从而F1∩F2是Rg-顶点割，由定理2，|F1∩F2|≥(n-g-1)(g+1)!.由于F2是g-好邻条件故障集，因此在Sn中F1F2的生成子图的最小度至少为g，即δ(Sn[F1F2])≥g.再由引理8，|F1F2|≥(g+1)!从而|F1|=|F1∩F2|+|F1F2|≥(n-g-1)(g+1)!+(g+1)!+(g+1)!=(n-g)(g+1)!>(n-g)(g+1)!-1，与假设|F1|≤(n-g)(g+1)!-1矛盾！

情况2F2F1≠∅且F1F2≠∅.

因为F1和F2是不可区分的，所以由定理1可知，要么V(Sn)=F1∪F2，要么V(Sn)(F1∪F2)与F1F2之间不存在边。分两种情况讨论。

子情况2.1V(Sn)=F1∪F2

当1≤g≤n-2时，(n-g)(g+1)!关于g是严格单调递增的，故由1≤g≤n-2且n≥4可知，n!=|V(Sn)|=|F1∪F2|=|F1|+|F2|-|F1∩F2|≤|F1|+|F2|≤2(n-g)(g+1)!-2≤2(n-(n-2))(n-2+1)!-2=4(n-1)!-2

子情况2.2V(Sn)≠F1∪F2

此时，V(Sn)(F1∪F2)与F1ΔF2之间无边。故F1∩F2是一个割。又因为F1和F2是g-好邻条件故障集，所以F1∩F2也是g-好邻条件故障集。从而F1∩F2是Rg-顶点割。由定理2可知，|F1∩F2|≥(n-g-1)(g+1)!.由于F2是g-好邻条件故障集，故在Sn中F1F2的生成子图的最小度至少为g，即δ(Sn[F1F2])≥g，由引理8，|F1F2|≥(g+1)!.从而|F1|=|F1∩F2|+|F1F2|≥(n-g-1)(g+1)!+(g+1)!=(n-g)(g+1)!>(n-g)(g+1)!-1，与假设|F1|≤(n-g)(g+1)!-1矛盾！

由定理3和定理4，可以推出下面的定理。

定理5设整数0≤g≤n-2，n≥4，那么在PMC模型下n维星图Sn中每一个顶点u的g-好邻局部诊断度tgl(u)=(n-g)(g+1)!-1.

定理6[10]对于一个图G，G的g-好邻诊断度tg(G)=min{tgl(u)|∀u∈V}.

推论1Sn的g-好邻诊断度tg(Sn)=min{tgl(u)|u∈V(Sn)}=(n-g)(g+1)!-1.其中0≤g≤n-2且n≥4.

3 总结

本文考虑了在PMC模型下星图Sn的每个顶点上的g-好邻局部诊断度，并证明了在PMC模型下，当0≤g≤n-2且n≥4时，星图Sn的每个顶点的g-好邻局部诊断度为(n-g)(g+1)!-1.因为星图具有顶点对称性，所以通过计算星图Sn中每个顶点的g-好邻局部诊断度可以进一步推导出星图的g-好邻诊断度。比较模型作为研究诊断度的经典模型，可以考虑在比较模型下星图Sn的每个顶点上的g-好邻局部诊断度。除此之外还可以在这两种经典模型下考虑其它著名网络拓扑的每个顶点的g-好邻局部诊断度。