李德华，芮绍平

（淮北师范大学 数学科学学院，安徽 淮北235000）

0 引言

信赖域方法最早由Powell［1］提出，具有较为理想的全局收敛性和稳定性.传统信赖域算法通常利用二次模型连续逼近目标函数，以期获得理想最优值.算法构建信赖域子问题

确定迭代步dk.其中：gk=∇f(xk)；Bk为Hesse矩阵∇2f(xk)的近似；Δk为信赖域半径；‖‖·是Euclidean范数.

信赖域方法就是通过这一比值ρk来衡量二次模型与目标函数的拟合程度.若ρk趋近于1，则表明目标函数的实际降幅与估计降幅接近，当前迭代效果好，需要考虑扩大下次迭代的信赖域半径；若ρk的值趋近于0或者小于0，表明迭代效果较差，试探步不可接受，需要缩小下次迭代的信赖域半径.

传统的信赖域方法根据比值ρk的大小放缩信任区域半径Δk，一般是原信任区域半径Δk常数倍增减，很大程度上依赖以往的经验来确定.为了克服这种缺陷，学者们引入自适应技术.Sartenaer［2］构造一类自动确定初始信赖域半径的ITTR算法.Zhang［3］等借鉴这一思想，把这种自适应策略应用到整个信赖域半径更新规则上.Hei［4］提出当前迭代的信赖域半径是关于比值ρk的R-函数与搜索步长‖ ‖dk-1的乘积.文献［3］给出信赖域半径的更新与Bk的关系.为了避免在每次迭代过程中计算矩阵Bk的逆，李改弟［5］提出新的信赖域半径更新规则，即，这里yk-1=gk-gk-1.在此基础上，文献［6-12］提出一些改进的自适应信赖域算法.

本文在基于李改弟［5］和Hei［4］的信赖域半径自动更新策略的基础上，把两者的更新策略结合起来，基于R-函数得到一个改进的信赖域半径自动更新策略.具体行文如下，在第2部分给出新算法，在第3部分证明新算法的收敛性，最后通过数据实验验证算法的稳定性与有效性.

1 算法

本节中，借助于R-函数，给出一个新的信赖域半径自动更新策略，并设计新算法.R-函数定义如下［4］：

定义1Rλ(t)定义在(-∞,+∞)上，参数λ∈(0,1)，C是一个常数集，R-函数Rλ(t)满足以下条件：

①Rλ(t)在(-∞,+∞)上是非减的；

③Rλ(t)≤1-r1（∀t∈λ，r1∈( 0,1-ζ)且r1∈C）；

④Rλ(λ)≤1+r2（r2∈( 0,+∞)且r2∈C）；

显然上述R-函数Rλ(t)（λ∈(0,1)）满足：

（i）0＜ζ≤Rλ(t)≤1-r1＜1,∀t∈(-∞,λ)；

（ii）1＜1+r2≤Rλ(t)≤M＜+∞,∀t∈[λ,+∞).

基于李［5］和Hei［4］的信赖域半径自动更新策略，本文提出一个改进的信赖域半径更新规则如下：

其中Rλ(ρk)是一个关于比值ρk的R-函数.新策略把Rλ(ρk)作为调节信赖域半径的依据，使得信赖域半径的变化取决于自身，基于此更新策略，设计算法1.

算法1（自适应线搜索信赖域算法）

步聚0取初始点x0∈Rn，对称阵B0∈Rn×Rn，ε＞0，0＜u＜1，Δ0=‖g0‖，0＜ζ＜1，0＜r1＜1-ζ，r2＞0，M＞1+r2，k:=0.

步骤1如果‖gk‖≤ε，则停止.否则转步聚2.

步骤2求解子问题（1）得到dk.

步骤3计算ρk的值.若ρk≥u，则令xk+1=xk+dk；否则求αk，使其满足Armijo准则，令xk+1=xk+αkdk，转步聚4.

步骤5更新矩阵Bk到Bk+1，令k:=k+1，转步聚1.

2 算法的收敛性分析

为证明算法收敛性，本文所需假设条件A如下：

（i）水平集L(x0)={x∈Rn|f(x)≤f(x0)}有界.

（ii）序列{Bk}一致有界，即∃M1＞0使得∀k有‖Bk‖≤M1.

引理1若当前迭代点xk是由算法1生成的，那么其中Mk=‖Bk‖

证明根据算法1步骤4所定义的信赖域半径，当前Δk满足关系式因此，根据是式（1）的一个可行解，则

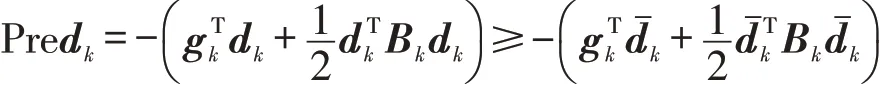
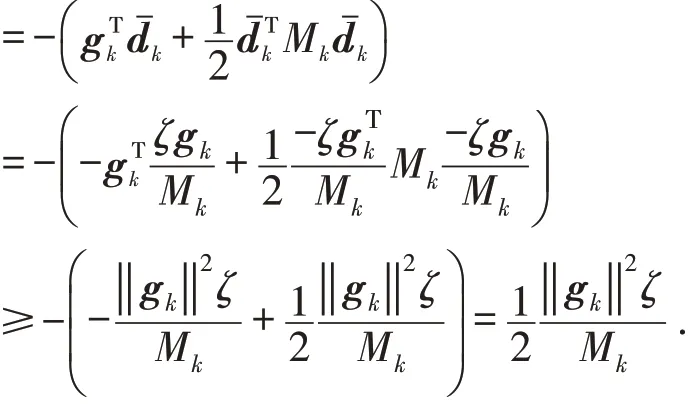
引理得证.

引理2［13］若试探步dk是子问题（1）的解，则有

定理1若假设A成立，算法1有限终止或迭代点列{xk}满足

证明由假设（i）可知，序列有下界.用反证法，假设定理1不成立.故存在εˉ＞0和一个无限子列满足.定义集合

根据引理1和算法1步骤3有

根据假设条件A可知，对任意的ki，一定存在M1＞0，使得Mki≤M1，且{f(xk)}有下界.故由式（5）可得到

也就是说，当ki(∈G)→+∞时，有为了不失一般性，假设对所有的ki∈G，都有着其中pki是前一次迭代到当前可接受的迭代间信赖域子问题计算的次数，所以对ζ都满足依据ζ的定义对应于下面的信赖域子问题不能接受

另一方面，根据引理2有

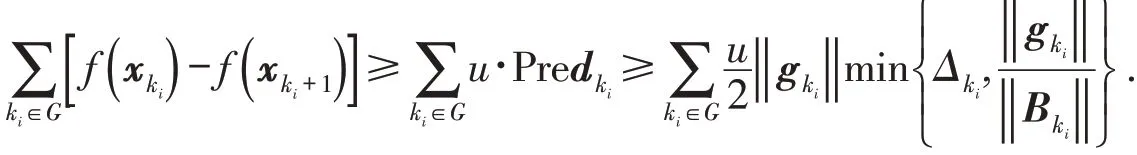
利用G的定义、假设A（ii）以及{f(xk)}单调递减有下界，可以得到Δki→0（ki∈G）.又

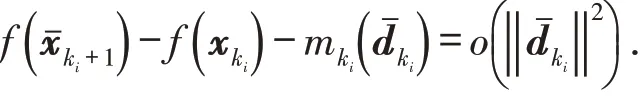
因此，对于充分大的ki∈G，

令ki→∞，有，这与式（7）矛盾.故假设错误，定理成立.

3 数据结果

本节给出算法1的数值实验，并和传统的牛顿型信赖域算法进行比较.为行文方便，把新算法和传统的信赖域算法分别记为ALG1和NTTR.ALG1中所取的R-函数为

其中参数取值为：γ1=γ2=0.01，ζ=0.1，u=0.25，M=5.两种算法都取相同初始信赖域半径Δ0=1，精度为ε=10-6.两种算法中测试函数均来自于文献［14］.

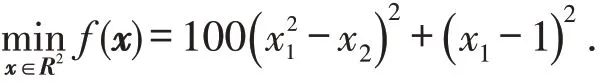
算法在Matlab9.0中编程实现，实验数据如下表：

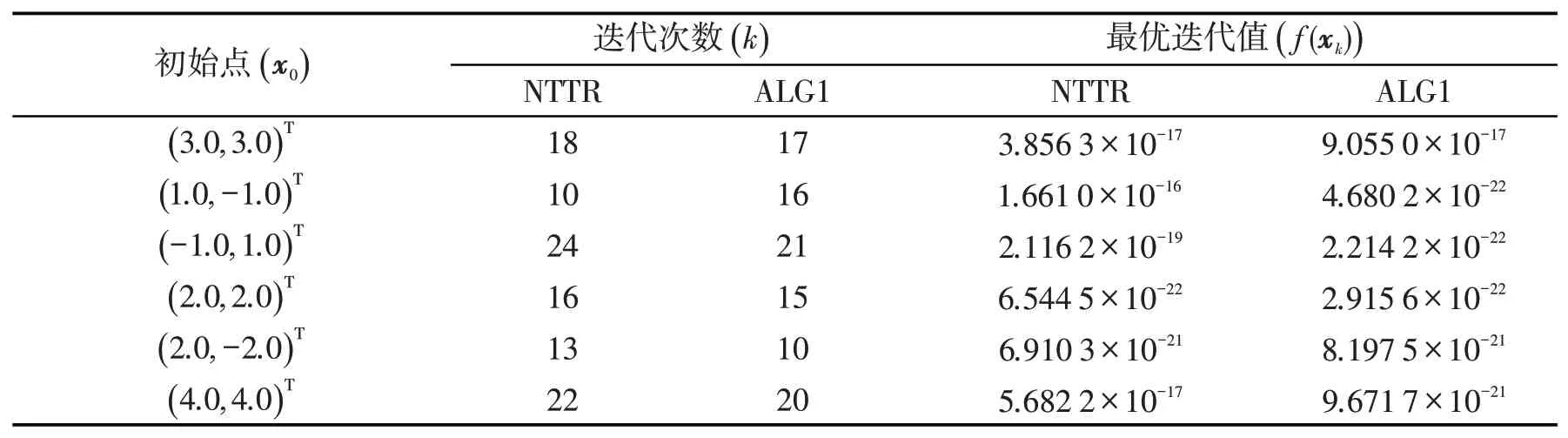
表1 数值结果

从数值结果可以看出，对于相同的初始点，算法1所需迭代次数比传统算法小，目标函数值下降的快，这表明算法1稳定有效.