形如a1+a2+···+an ≥(=,≤)f(n)、a1a2·····an≥(=,≤)g(n)的数列前n项和、积型不等式、等式的证明问题，在高考及竞赛试题中时有出现.此类问题涉及函数、数列、不等式等高中数学的核心内容，是高考及竞赛的一个热点和难点.解决此类问题的通常方法是放缩法、数学归纳法和利用数列单调性等，方法较难较繁，对考生的能力有较高的要求.若从数列的观点看，上述两式的左边分别是数列{an}的前n项和、积，若把f(n),g(n)分别视为数列{bn}的前n项和、积，(若f(n)=c(非零常数)，可把c视为无穷等比数列{bn}的前n项和Bn的极限即所有项和B)，则问题的实质是两个数列{an}与{bn}的前n项和或积的不等或相等问题，从而只要通过比较数列{an},{bn}的通项an,bn的大小即可.这样就把证明两个数列前n项和、积的不等、相等关系降格为证明相应通项的不等、相等关系，从而可使问题化难为易，化繁为简.兹举例说明.

1.把证明两数列前n 项和、积的相等关系降格为证明相应通项的相等关系

例1(《数学》选修2-2(湖南版)第140 页第9(3)题)证明：

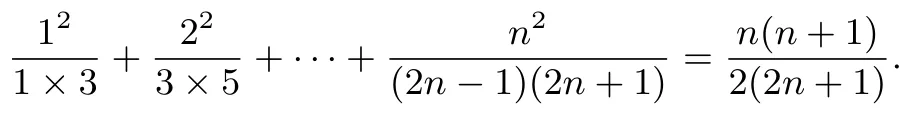
简析记原式左右两边分别为数列{an},{bn}的前n项 和An,Bn，则bn=Bn -2)，并且也适合上式，则bn=(为节省篇幅，以下各例将略去这一步).于是有an=bn(n ∈ℕ∗，从而可得An=Bn，即原式成立.

例2(ⅠMO-8试题)对于一切正整数n及每个实数(k= 0,1,··· ,n,m是任意整数)，求证：

简析记原式左右两边分别为数列{an},{bn}的前n项和An,Bn，则

且b1=B1= cotx-cot 2x=也适合上式.则有an=bn(n ∈ℕ∗),从而可得An=Bn，即原式成立.

例3证明cosxcos 2x·····cos 2n-1

简析记原式左右两边分别为数列{an},{bn}的前n项乘积An,Bn，则an=cos 2n-1x，

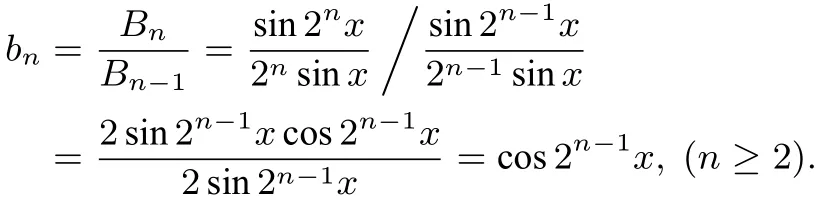
且易求得b1=B1= cosx也适合上式.则有an=bn(n ∈ℕ∗)，从而得An=Bn，即原式成立.

例4(2018年高考天津卷理科第18 题)设数列{an}是等比数列，公比大于0，其前n项和为Sn(n ∈ℕ∗)，{bn}是等差数列，已知a1=1,a3=a2+2,a4=b3+b5,a5=b4+2b6.

(Ⅰ)求{an}和{bn}的通项公式;

(Ⅱ)设数列{Sn}的前n项和为Tn(n ∈ℕ∗)，(1)求Tn;(2)证明

简析(Ⅰ)an=2n-1,bn=n(过程从略).

(Ⅱ)(1)Tn=2n+1-n-2(过程从略).

(2)记原式左右两边分别为数列{cn},{dn}的前n项和Cn,Dn，则dn=Dn - Dn-1=且易求得也适合上式.则有cn=dn(n ∈ℕ∗)，从而得Cn=Dn，即原式成立.

2.把证明两数列前n 项和、积的不等关系降格为证明相应通项的不等关系

例5(2016年高考四川卷理科第19 题)已知数列{an}的首项为1,前n项和为Sn,Sn+1=qSn+1，其中q ＞0,n ∈ℕ∗.

(1)若2a2,a3,a2+2 成等差数列，求数列{an}的通项公式;

简析(1)an=qn-1(过程略).(2)记原不等式的左右两边分别为数列{en},{bn}的前n项和En,Bn，则(n ≥2),且易求得b1=B1= 1 也适合上式，en=又由可解得则(n ∈N∗),从而得En ＞Bn即原不等式成立.

例6(2010年高考湖北卷理科第21 题改编)已知函数的图像在点(1,f(1))处的切线为y=x-1.

(1)用a表示b,c;

(2)若f(x)≥lnx在区间[1,+∞)上恒成立，求a的取值范围;

简析(1)b=a-1,c=1-2a.(2)(过程从略).

(3)记原不等式左右两边分别为数列{an},{bn}的前n项和An,Bn，则

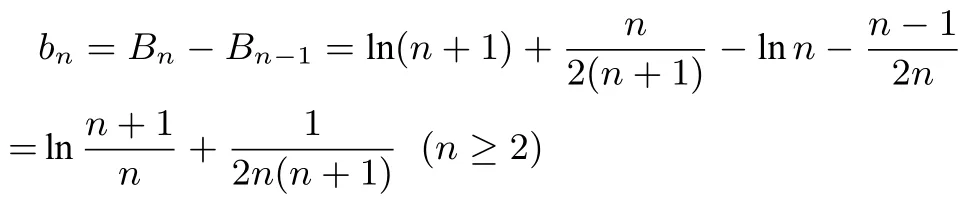
例7(2018年成都市第二次诊检试题理科第21 题)已知函数f(x)=xlnx+ax+1,a ∈ℝ.

(1)当x ＞0 时，若关于x的不等式f(x)≥0 恒成立，求a的取值范围;

(2)当n ∈ℕ∗时，证明：

简析(1)a ≥-1(过程从略).

(2)记原不等式的左中右三部分分别为数列{cn},{an},{bn}的前n项和Cn,An,Bn，则易求得cn=且也分别适合上两式.由(1)知，当a=-1 时，得据此可得

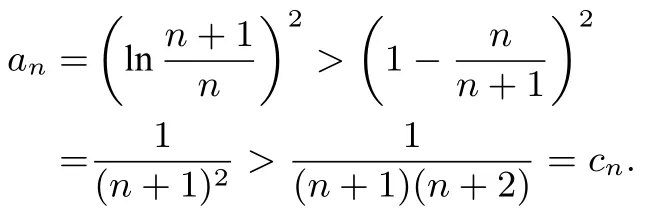
又

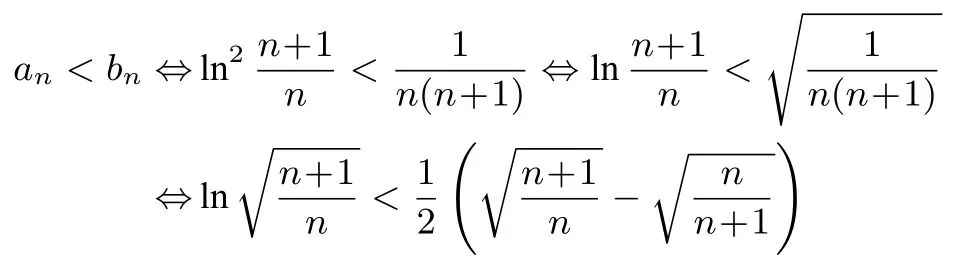
例8(2009年高考山东卷理科第20 题)已知等比数列{an}的前n项和为Sn，对任意的n ∈ℕ∗点(n,Sn)均在函数y=bx+r(b ＞01,r均为常数)的图像上.

(1)求r的值;

(2)当b= 2 时，记bn= 2(log2an+1)(n ∈ℕ∗),证明对任意的成立.

简析(1)略.(2)易求得an= (b -1)bn-1,则b= 2时，an= 2n-1,bn= 2(log22n-1+1)= 2n.记原不等式左右两边分别为数列{cn},{dn}的前n项积Cn,Dn，则且也适合上式.由于

则cn ＞dn(n ∈ℕ∗)，从而得Cn ＞Dn，即原不等式成立.

例9(2014年高考全国Ⅱ卷理科第17 题)已知数列{an}满足a1=1,an+1=2an+1.

简析(1)(过程从略).

(2)记原不等式左边为数列{cn}的前n项和Cn，则由于可把右边视为首项b1=c1= 1,公比的无穷等比数列{bn}的前n项和Bn的极限，即所有项和B，则bn=1·进而得Bn ＜B,故只要证明cn ≤bn即可.

类似地，容易解决2012年高考广东卷第19 题：

已知数列{an}的前n项和Sn满足2Sn=an+1-2n+1+1,n ∈ℕ∗,且a1,a2+5,a3成等差数列.

(1)求a1;

(2)求an;

(3)证明对一切正整数n，有(提示： (1)a1=1;(2)an=3n-2n;(3)

例10(2011年天津市预赛试题)已知数列{an}定义为a1=1,an+1=2an+

(1)证明： 当n ＞1 时，an+1+an-1=4an;

简析(1)略.(2)可求得其中(过程从略).记原不等式左边为数列{cn}的前n项和Cn，则由于

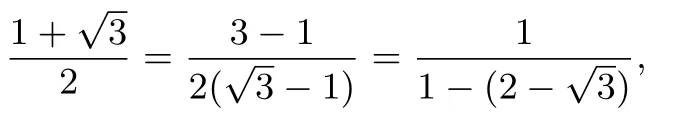
可把右边视为首项b1=c1= 1，公比的无穷等比数列{bn}的前n项和Bn的极限，即所有项和B，则进而得Bn ＜B.由于

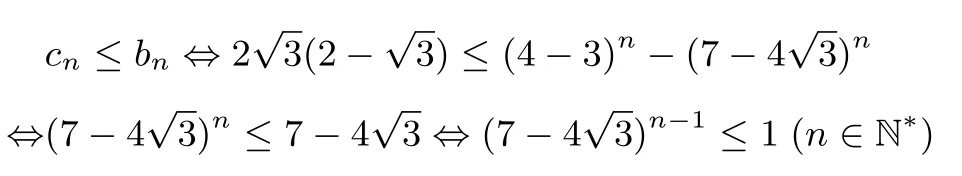
则有Cn ≤Bn ＜B，即原不等式成立.

3.把比较两数列前n 项和、积的大小降格为比较相应通项的大小

例11(1998年高考试题)已知{bn}是等差数列，b1=1,b1+b2+···+bn=145,

(1)求数列{bn}的通项公式;

(2)数列{an}的通项公式前n项和为Sn，试比较Sn与的大小，并证明你的结论.

简析(1)bn=3n-2(过程从略).

(2)记数列{cn}的前n项和

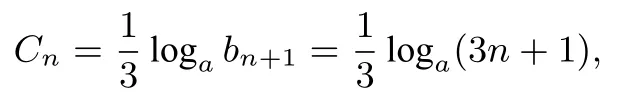
易求得

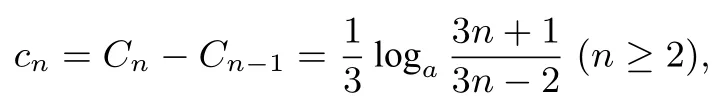
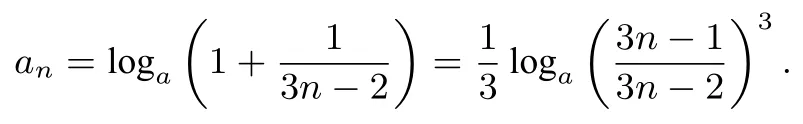
由于

则a ＞1 时，an ＞cn可得;当0＜a ＜1时，an ＜cn可得

方法总结对于形如a1+a2+···+an ≥(=,≤)f(n)和a1a2·····an ≥(=,≤)g(n)的不等式、等式的证明步骤是： (1)记原不等式左右两边分别为数列{an},{bn}的前n项和An,Bn;(2)利用b1=B1,bn=Bn-Bn-1(n ≥2)或求出bn(n ∈ℕ∗);(3)比较an与bn的大小关系，进而得到An与Bn的大小关系.

对于形如a1+a2+···+an ＞(＜)c(c为非零常数)的不等式的证明步骤是： (1)记原不等式左边为数列{an}的前n项和An; (2)把c写成的形式，记右边为首项b1=a1、公比为q的无穷等比数列{bn}的前n项和Bn的极限(即所有项和)B，得bn=bqn-1;(3)若an ≤bn且b1＞0,q ＞0,则可得An ≤Bn ＜B;若an ≥bn且b1＜0,q ＞0，则可得An ≥Bn ＞B

上文对一类和、积型数列等式、不等式问题的降格处理的方法，不仅行之有效，而且思路清晰，易于操作，过程简捷，使一些较高难度的高考、竞赛试题变得简单易行，体现了转化与降维等数学思想方法的魅力，不失为一种值得推广的好方法.