北京市第十二中学(100071) 刘 刚

1.试题

真题(2019年高考全国Ⅱ卷理科第21 题)已知点A(-2,0)、B(2,0)，动点M(x,y)满足直线AM与BM的斜率乘积为记M轨迹为曲线C.

(1)求C的方程，并说明C是什么曲线？

(2)过坐标原点的直线交C于P、Q两点，点P在第一象限，PE⊥x轴，垂足为E，连接QE并延长交C于点G.(i)证明： ∆PQG是直角三角形;(ii)求∆PQG面积的最大值.

试题考查了曲线的方程、直线和椭圆的位置问题以及最值问题，考查了学生分析问题与解决问题的能力，体现了逻辑推理、直观想象、数学运算等数学核心素养.试题解法灵活，内涵丰富，综合性强，为不同学生搭建了施展才能的舞台，是一道好题.

2.解法探究

解答(1)C的方程是C是中心在坐标原点，焦点在x轴上的椭圆，不含左、右顶点，过程从略.

(2)解法1 (i)设直线PQ的斜率为k，则其方程为y=kx(k ＞0)，与C的方程联立，解得则P(u,uk)，Q(-u,-uk),E(u,0)，于 是直线QG的斜率为方程为将其与C的方程联立，得

设G(x0,y0)，则-u和x0是方程①的解，所以x0=由此得从而直线PG的斜率为

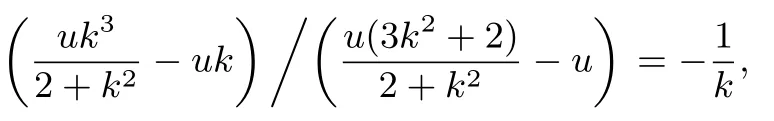
所以PQ⊥PG，故∆PQG是直角三角形.

(ii)由(i)得所以∆PQG的面积

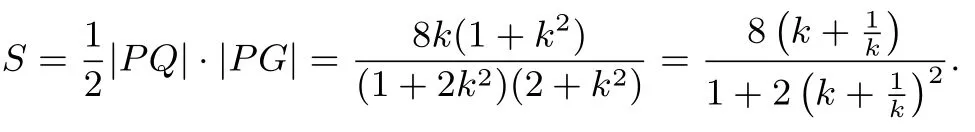
点评解法1 第(i)问以直线PQ的斜率k为研究对象，先联立直线PQ与C的方程，并为了表达简便，设出进而得到点P,Q,E的坐标，在此基础上求出直线QG的方程并与C的方程联立，然后运用韦达定理得到点G的坐标，最后借助斜率完成解答，体现了坐标法的应用;第(ii)问在第(i)问的基础上先表示出∆PQG的面积，然后化简、换元，最后借助函数的单调性求得最值，体现了解析几何与不等式、函数交汇的特点.

解法2 (i)设由已知得E(2 cosα,0)，所以

因 为Q,E,G三点共线，所以共线，即整理得2 cosαsinβ-sinαcosβ+cosαsinα=0，于是cosα(sinα+sinβ)=sin(α-β)，即

由此得

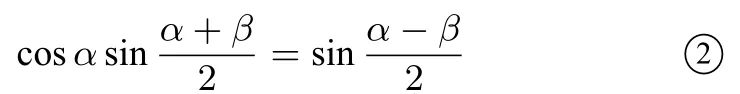
因 为所以

由 ②得

(ii)如图1，连接OG，由椭圆的对称性，知 ∆PQG的面积S∆P QG= 2S∆OP G.因为所以

图1

kOP=且OP ⊥GP，所以

kGP ·kOP=解得设所以

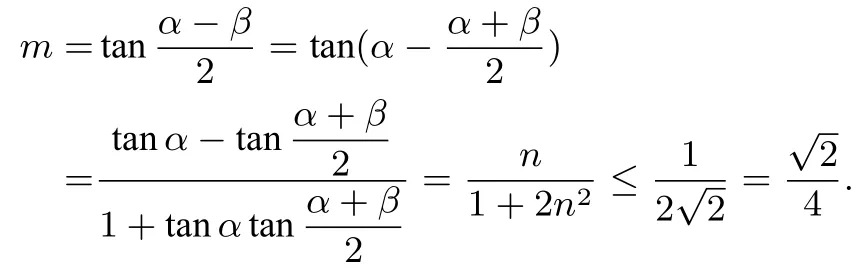
点评解法2 借助椭圆的参数方程进行求解，解答时应熟练掌握三角公式，同时对学生的逻辑推理、数学运算等素养要求较高.另外，在第(ii)问中用到了三角形面积公式的坐标表示： 若O(0,0),A(x1,y1),B(x2,y2)，则

解法3 (第(i)问的简便解法)设P(x1,y1)(x1＞0,y1＞0)，G(x2,y2)，则Q(-x1,-y1),E(x1,0).因 为P(x1,y1),G(x2,y2)在C上，所以两式作差，得即因为Q,E,G三点共线，所以kQE=kQG，即

又kP G · kP Q=把③代入，得所以PQ ⊥PG，故∆PQG是直角三角形.

点评解法3 以点P,Q的坐标为研究对象，运用点差法得到了,接下来借助斜率将Q,E,G三点共线问题转化为坐标之间的关系，得到了在此基础上完成解答，简化了运算，体现了设而不求、转化的数学思想方法.

3 推广

将试题一般化，并从逆向考虑，得到了下面一组性质.

性质1已知椭圆C:= 1(a ＞b ＞0)，过坐标原点的直线交C于P,Q两点，点P在第一象限，PE ⊥x轴，垂足为E，连接QE并延长与C交于点G，则PG ⊥PQ的充要条件是a2=2b2.

性质2已知椭圆C:= 1(a ＞b ＞0)，过坐标原点的直线交C于P,Q两点，点P在第一象限，PE ⊥x轴，垂足为E，过P作PG ⊥PQ，与C交于另一点G，则Q,E,G三点共线的充要条件是a2=2b2.

证明设P(x1,y1)(x1＞0,y1＞0)，G(x2,y2)，则Q(-x1,-y1),E(x1,0).因为P(x1,y1),G(x2,y2)在C上，所以两式作差，得即kP G=因为且PG ⊥PQ，所以即所以因为所以Q,E,G三点共线，故命题成立.

性质3已知椭圆过坐标原点的直线交C于P,Q两点，点P在第一象限，过P作PG ⊥PQ，与C交于另一点G，直线QG与x轴交于点E，则PE ⊥x轴的充要条件是a2=2b2.

性质4已知椭圆，过坐标原点的直线交C于P,Q两点，点P在第一象限，PE ⊥x轴，垂足为E，连接QE并延长与C交于点G，设直线PQ,PG的斜率分别为k1,k2，则

(性质1，3，4 的证明请读者自行完成，限于篇幅不再赘述.)

性质5已知椭圆过坐标原点的直线交C于P,Q两点，点P在第一象限，过P作PG ⊥PQ，与C交于另一点G，直线QG与x轴交于点E，设C的离心率为e，若则PE ⊥x轴;若设直线QG,PE的斜率分别为k1,k2，则k1=(1-2e2)k2.

证明若，则a2= 2b2，由性质3可得PE ⊥x轴.若则a22b2，设Q(x1,y1)(x1＜0,y1＜0),G(x2,y2)，则P(-x1,-y1).设直线QG的方程为y=k1x+m，与C的方程 联立，得

(b2+k21a2)x2+2k1ma2x+a2m2-a2b2=0,所以因为

kP Q=且PG ⊥PQ，所以解得又因为所以于是因为所以

性质6已知椭圆过坐标原点的直线交C于P,Q两点，点P在第一象限，过P作PG ⊥PQ，与C交于另一点G，设∆PQG的面积为S，若则S有最大值为ab;若则S有最大值为其中c2=a2-b2.

证明设直线PQ的斜率为k，则其方程为y=kx(k ＞0)，与C的方程联立，解得

记

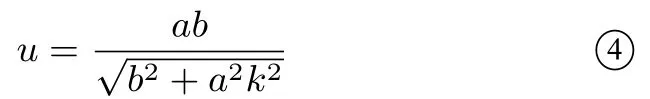
则P(u,uk).因为PG ⊥PQ，所以直线PG的斜率为则其方程为与C的方程联立，得(a2+k2b2)x2-2u(k2+ 1)a2x+a2u2(k2+1)2-k2a2b2= 0，所以解得于是

因为所 以S=把④代 入，得S=设则由k ＞0，得t ≥2，当且仅当k= 1 时取等号.若即则有当且仅当时等号成立，故S有最大值为ab.若即则有在[2,+∞)上单调递增，所以当且仅当t= 2 时，S取得最大值为综上，结论成立.

以上对一道2019年高考解析几何试题从不同角度进行了探究，从而将试题的价值最大化.当然，还可以运用类比的方法研究双曲线中的相关结论，感兴趣的读者不妨一试.高考试题是集体智慧的结晶，具有基础性、典型性、创新性、导向性等特点，只有认真研究这些试题，才能在高三复习中少走弯路，真正提高教学效率.在高三复习中，首先要引导学生回归课本，落实基础知识.这道高考试题的背景就来源于教材，教材是学生复习时最重要的参考资料.其次要注重基本思想方法的积累与训练.坐标法是解析几何的基本方法，解题时要选准研究对象，并将几何条件坐标化，然后再进行数学运算从而将问题解决.再者要努力培养学生的数学核心素养.在平时教学中，要以新课标理念为导向，坚持提高学生的核心素养，这样才会水到渠成，在高考中取得优异的成绩.

以下试题供读者练习.

练习1(2011年高考江苏卷第18 题)如图2，在平面直角坐标系xOy中，M,N分别是椭圆的顶点，

过坐标原点的直线交椭圆于P,A两点，其中P在第一象限，过P作x轴的垂线，垂足为C，连接AC，并延长交椭圆于点B，设直线PA的斜率为k.

(1)当直线PA平分线段MN时，求k的值;

(2)当k=2 时，求点P到直线AB的距离d;

(3)对任意k ＞0，求证：PA ⊥PB.

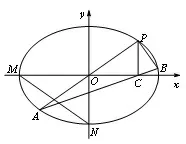
图2

练习2(2012年高考湖北卷理科第21 题)设A是单位圆x2+y2= 1 上的任意一点，l是过点A与x轴垂直的直线，D是直线l与x轴的交点，点M在直线l上，且满足|DM|=m|DA|(m ＞0 且1).当点A在圆上运动时，记点M的轨迹为曲线C.

(Ⅰ)求曲线C的方程，判断曲线C为何种圆锥曲线，并求焦点坐标;

(ⅠⅠ)过原点且斜率为k的直线交曲线C于P,Q两点，其中P在第一象限，它在y轴上的射影为点N，直线QN交曲线C于另一点H，是否存在m，使得对任意的k ＞0，都有PQ ⊥PH？若存在，求m的值;若不存在，请说明理由.

练习3 (2014年高考山东卷文科第21 题)在平面直角坐标系xOy中，椭圆的离心率为直线y=x被椭圆C截得的线段长为

(Ⅰ)求椭圆C的方程; (ⅠⅠ)过原点的直线与椭圆C交于A,B两点(A,B不是椭圆C的顶点).点D在椭圆C上，且AD ⊥AB，直线BD与x轴、y轴分别交于M、N两点.(i)设直线BD,AM的斜率分别为k1,k2，证明存在常数λ使得k1=λk2，并求出λ的值;(ii)求∆OMN面积的最大值.

参考答案1.(1);(3)略.

3.(Ⅰ);(ⅠⅠ)(i)