Exact Solutions of an Alice-Bob KP Equation∗
2019-07-16WenBiaoWu吴文标andSenYueLou楼森岳
Wen-Biao Wu(吴文标)and Sen-Yue Lou(楼森岳),2,†
1School of Physical Science and Technology,Ningbo University,Ningbo 315211,China
2Shanghai Key Laboratory of Trustworthy Computing,East China Normal University,Shanghai 200062,China
AbstractAn Alice-Bob Kadomtsev-Petviashivili(ABKP)equation with shifted-parity(parity with a shift for the space variable x)and delayed time reversal(,time reversal with a delay)symmetries is investigated.The multi-soliton solutions with three arbitrary even or odd functions are found from thesymmetry reductions of a coupled local KP system.The result shows that for the ABKP equation withnonlocality,the odd numbers of solitons are prohibited.The solitons of the ABKP must be paired.For the ABKPII equation,there exists a critical value of wave numbers for the existence of paired solitons.For the ABKPI equation,there are two types of“breather” excitations.A lump solution of the ABKPI may possess four, fi ve or six leaves.
Key words:nonlocal systems,KP equations,parity and time reversal,classical prohibition
Since Ablowitz and Musslimani[1]introduced an integrable nonlocal nonlinear Schrödinger equation

where the operatorsˆP andˆC are the usual parity and charge conjugation,the study of the nonlocal system becomes one of the hot topics in nonlinear science.[2−12]
It is well known that there are various correlated and/or entangled events that may be happened in different times and places. To describe two-place physical problems,Alice-Bob(AB)systems[10]are proposed by using the shifted parity(ˆPs),delayed time reversal(ˆTd)and charge conjugate(ˆC)symmetries.In addition to the nonlocal nonlinear Schrödinger equation(1),there are many other types of two-place nonlocal models,such as the nonlocal KdV systems,[12]the nonlocal modified KdV systems,[4−5,13]the discrete nonlocal NLS systems,[6]the coupled nonlocal NLS systems[2]and the nonlocal Davey-Stewartson systems,[7−9]etc.Especially,in Ref.[10],one of us(Lou)proposed a series of integrable AB systems including the ABKdV systems,ABmKdV systems,[13]ABKP systems,AB-sine Gordon(ABsG)systems,ABNLS systems,AB-Toda(ABT)systems,and ABAKNS systems.
In addition,Lou established a most general ABKdVequation and presented itsinvariant Painlev´e II reduction and soliton-cnoidal periodic wave interaction solutions for the ABKdV system.[11]In this letter,by using the idea of Refs.[11–12]we investigate a special ABKP system
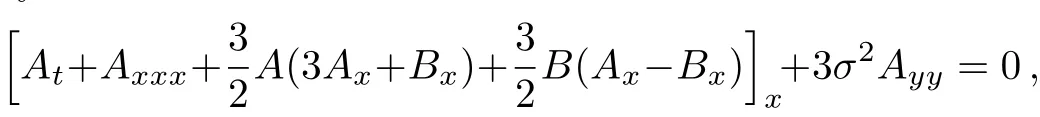

with arbitrary constants x0,t0,and y0.
The ABKP system Eq.(2)can be derived by applying the consistent correlated bang(CCB)approach to the usual KP equation as follows in Ref.[11].
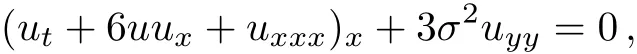
It is known that ifˆg is a second order operator,then an arbitrary function A can be separated to an invariant part and an antisymmetry part in the following way
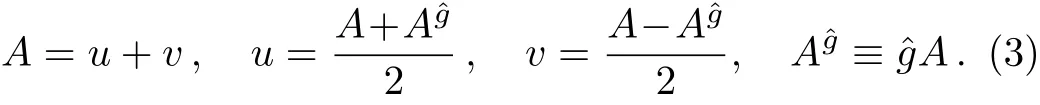
To solve the ABKP system(2),we can takeEq.(3).Thus,the ABKP equation(2)becomes

with
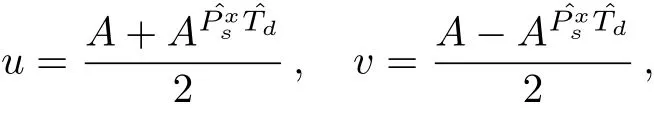
and the trivial properties

In other words,to solve the ABKP Eq.(2)is equivalent to solve the integrable coupling(4)and(5)with the parity conditions(6).
For the KP Eq.(4),it is well known that the multiple soliton solution possesses the form[14]


where the summation of ν should be done for all permutations of νi=0,1,i=1,2,...,N and
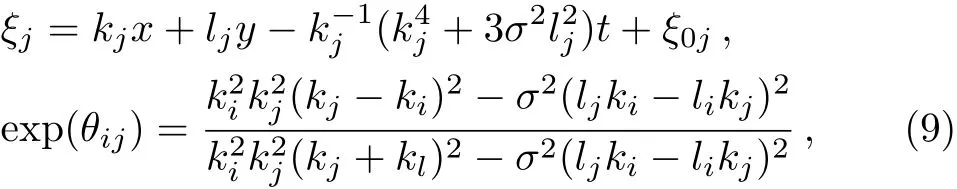
with arbitrary constants ki,li,and ξi0for all i.
From the expression(7)with(8)it is quite difficult toinvariant form.Fortunately,from the results of Ref.[10],we know that if we rewrite Eq.(9)as
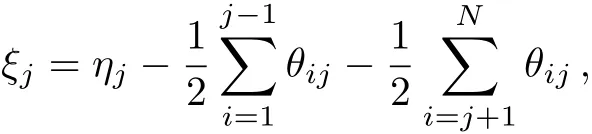
where
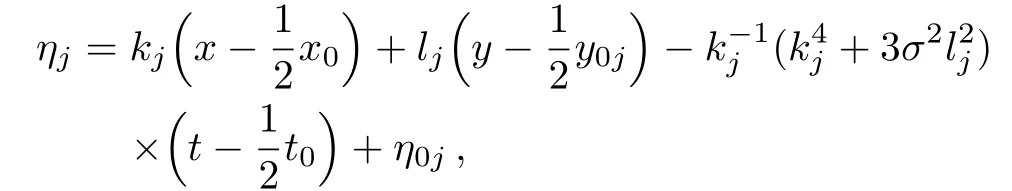
with arbitrary constants y0jand η0j,then the N-soliton solution of the KP Eq.(4)can be rewritten as[10]
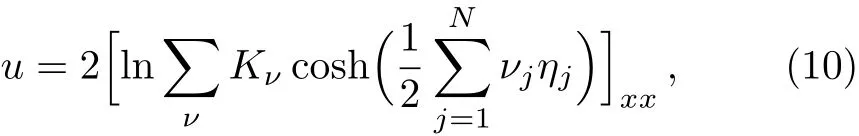
where the summation of ν={ν1,ν2,...,νN}should be done for all non-dual permutations of νi=1,−1,i=1,2,...,N(ν and ν′are dual if ν = −ν′),and
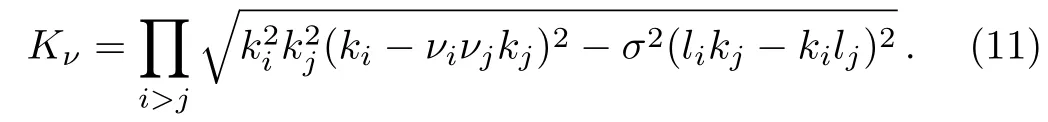
Similar to the AB-Boussinesq case,[15]the odd numbers of the multi-soliton solution are prohibited by the parity and time reversal condition(6).
For the even numbers of multi-soliton solutions,the paired conditions

For{n=1,N=2}and{n=2,N=4},we have(after rule out common constants for simplicity)
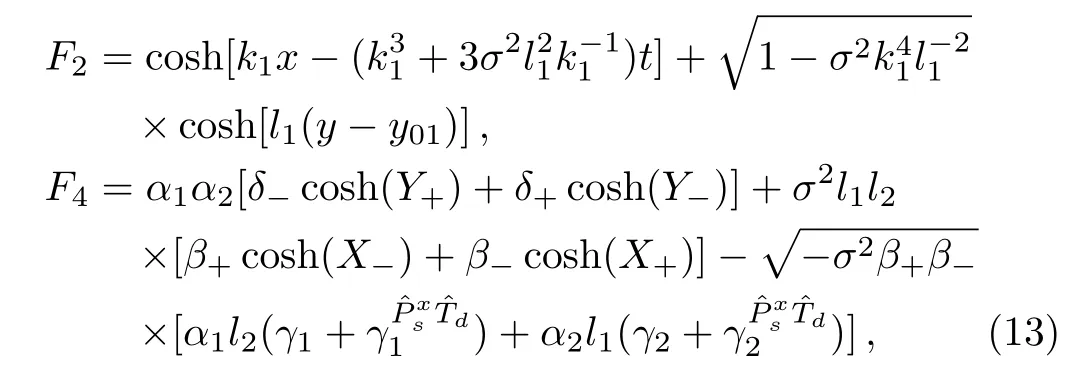
where the variables X±,Y±,γ1,and γ2are defined by

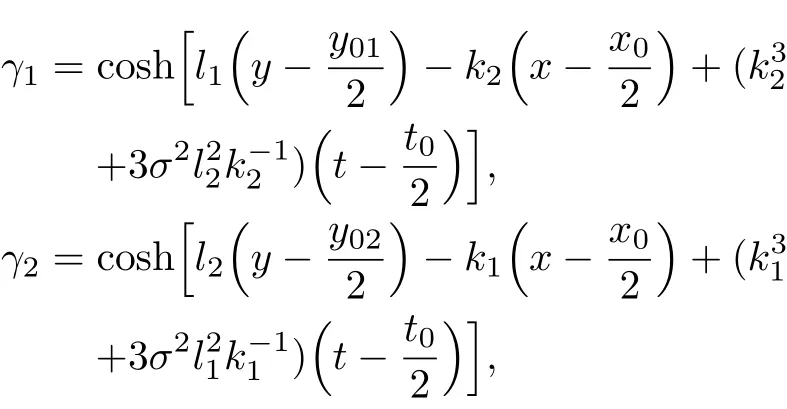
and the constants α1,α2,β±,and δ±are related to arbitrary constants k1,k2,l1,and l2by
Whence the u field Eq.(4)is solved.The v field equation can be solved via known symmetries of the KP equation after considering the antisymmetric condition(6).It is clear that for any given solution u,say,the multi-soliton solution(10),there exist infinitely many solution v.Here we write down a special one,
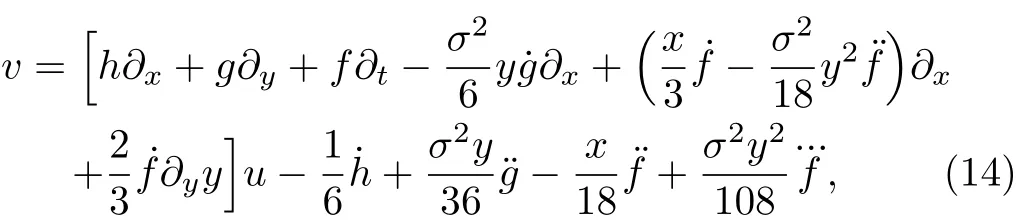
with f,g,and h being arbitrary functions of t.To satisfy theˆPxsˆTdantisymmetric condition of v,The functions f,g,and h in Eq.(14)should satisfy

In other words,the functions f and h are arbitrary even functions and g is an arbitrary odd function with respect to time t.
Finally,we get a multi-soliton solution of the ABKP equation(2),

with the relations(11)and(12).When the arbitrary functions f,g and h are all taken as zeros,the solution(15)becomesˆPxsˆTdinvariant.For any nonzero f,g and h,the solution(15)is a symmetryˆPxsˆTdbreaking one.
Figure 1 displays the paired two soliton solution(15)with the parameters{n=1,k2=−k1=1,l2=l1=2,x0=t0=y01=0}and function selections{f=g=0,h=2}at time t=0 for the ABKPI(σ2= −1)equation.
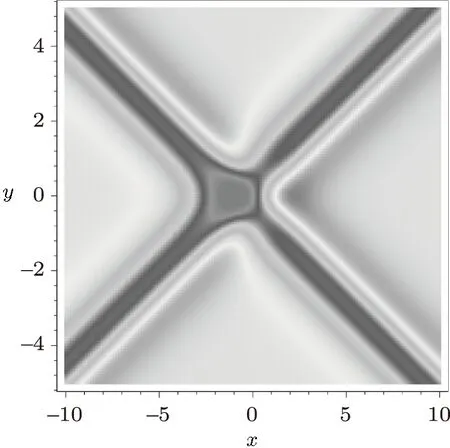
Fig.1 (Color online)Two soliton interaction solution for the ABKPI equation.
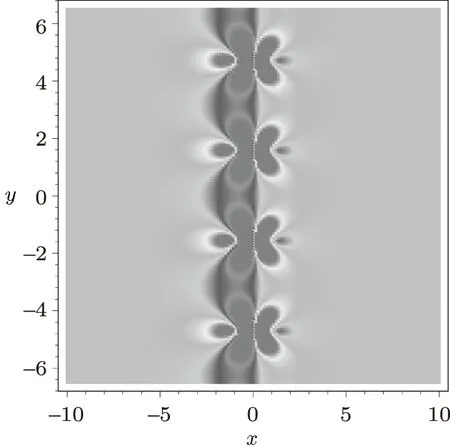
Fig.2 (Color online)The y-breather plot for the ABKPI equation expressed by Eq.(1√5)with the parameters{n=1,k2= −k1=1,l2=l1=,x0=t0=y01=0}and function selections{f=g=0,h=2}at time t=0.
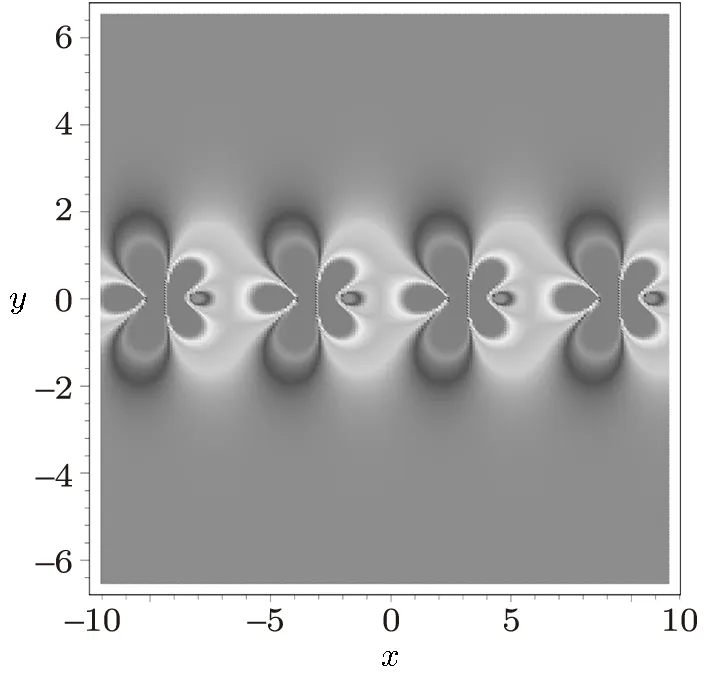
Fig.3(Color online)The density plot of the x-breather for the ABKPI equation expre√ssed by Eq.(15)with the parameters{n=1,k2=−k1=,l2=l1=2,x0=t0=y01=0}and function selections{f=g=0,h=2}at time t=0.
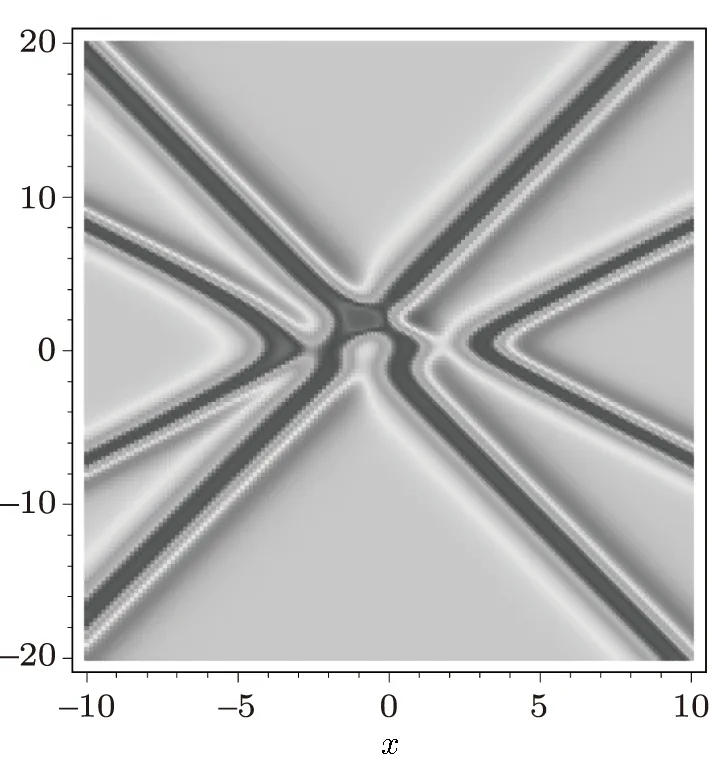
From the expression(13),we know that there exists a further prohibition for the ABKPII(σ2=1),the paired soliton is valid only for Fig.4 (Color online)The lump structures(15)for the ABKPI system(2).The parameter and function selections are given by Eq.(16)at time t=0 while the function h is fixed as(a)h=0 for four leaf lump,(b)h=2.2 for fi ve leaf lump and(c)h=300 for six leaf. For the ABKPI system,from(13)we know also that both k1and l1can be pure imaginary.If k1is real and l1is imaginary and k14<|l1|2,then the expression(13)related solution A becomes an analytic y-breather(periodic solution in the y direction)for the ABKPI equation.Figure 2 displays the y-breather structure expressed by Eq.(15)with the same parameter a√nd function selections as those in Fig.1 except for l1= If k1is imaginary and l1is real,then the expression(13)related solution A becomes an analytic x-breather(periodic solution in the x direction)for the ABKPI equation.Figure 3 shows the x-breather structure expressed by Eq.(15)with the same parameter and function selections as those in Fig.1 except for From Figs.2 and 3,we can conclude that whence the period of the x-breather and/or y-breather tends to infinity,the breathers will become a special lump solution of the ABKP equation(2).In fact it is quit trivial to check the ABKP system(2)possesses a lump-type solution(15)with for arbitrary constants c and y0. Figure 4 displays three different structures for the ABKPI equation under the parameter and function selections while h is taken as h=0,h=2.2,and h=300 for Figs.4(a)–4(c)respectively. Figure 5 exhibits the interaction behavior for the ABKPI equation expressed by Eq.(15)with the parameter selections{n=2,l1=−l3=1,l2= −l4=2,k3=k1=k4=k2=2,x0=t0=y01=0,y02=1}and the function selections{f=g=0,h=1}at time t=0. Fig.5 The density plot of the four-soliton interaction solution of the ABKP equation(2)with σ2= −1. In summary,in this paper,a special ABKP system with PxsTdnonlocality is investigated. Some types of multi-soliton solutions including paired solitons,x-and y-breathers and lumps are obtained.The soliton structures of the ABKP systems are quite different from those of the usual KP system.The more about the AB systems and the multi-place systems[16]should be further studied.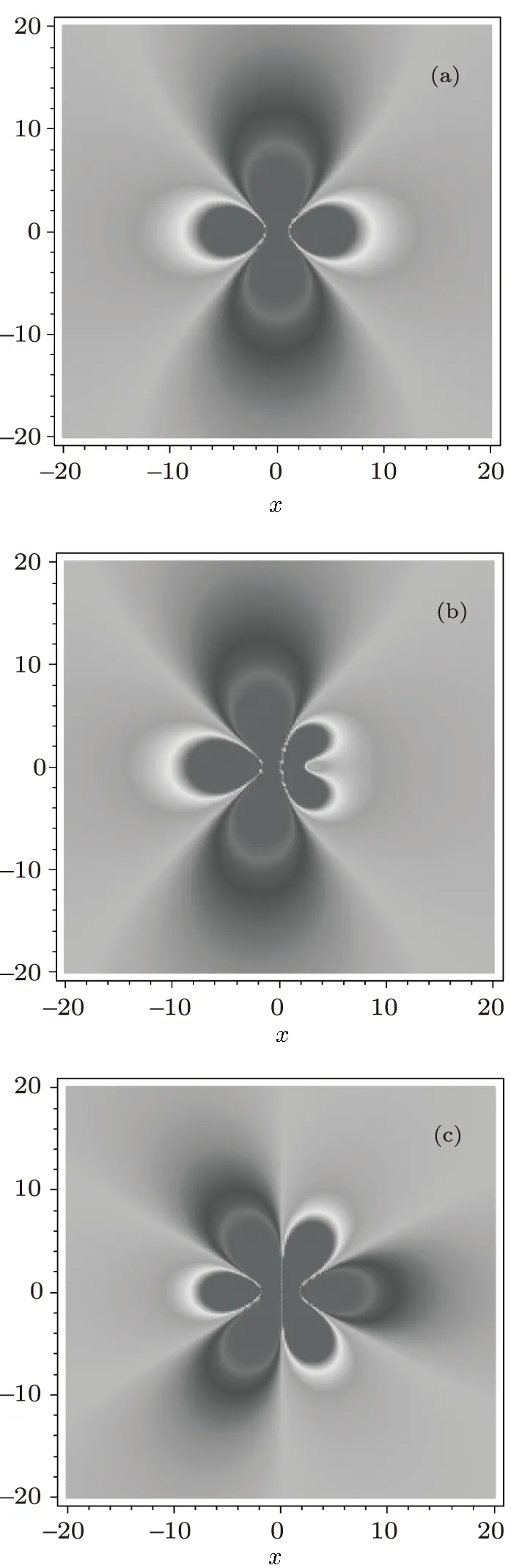

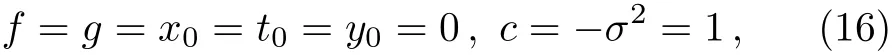
杂志排行
Communications in Theoretical Physics的其它文章
- Interactions of Lump and Solitons to Generalized(2+1)-Dimensional Ito Systems∗
- Solution of the Dipoles in Noncommutative Space with Minimal Length∗
- General Solution for Unsteady Natural Convection Flow with Heat and Mass in the Presence of Wall Slip and Ramped Wall Temperature
- Lump Solutions for Two Mixed Calogero-Bogoyavlenskii-Schi ffand Bogoyavlensky-Konopelchenko Equations∗
- A Spinor Approach to the SU(2)Clebsch-Gordan Coefficients∗
- Analysis on Lump,lumpoffand Rogue Waves with Predictability to a Generalized Konopelchenko-Dubrovsky-Kaup-Kupershmidt Equation∗
