一类水污染问题中可扩散界面的适定性研究*
2019-04-11张付臣
李 季, 张付臣
(重庆工商大学 数学与统计学院,重庆 400067)
0 引 言
当今社会,淡水资源严重稀缺,甚至很多地区水资源严重缺乏,虽然长江流域附近有着长江提供大量的水资源,但是随着社会的发展,工农业的发展,水污染越来越严重,例如工厂污水的排放,过往船只丢弃的废弃物,甚至江边居民丢弃的各种污染物都会不同程度地对长江流域水资源造成污染。如何清理长江中的水污染以及如何计算出已经被污染部分与未被污染部分之间的临界面就变得非常重要[1-6]。成功找到临界面,一方面能够防止污染的继续,让未被污染的水层保证不被继续污染,另一方面也可以采取各种方式对已经被污染的水资源进行处理,合理利用这部分水资源做其他用处[7-11]。该文章就是在这种背景下,通过假设污染水层与未污染水层不能进行物质交换,并且两者之间的临界面为可扩散临界面的情况下建模,研究该临界面的存在性。水层结构如图1所示。
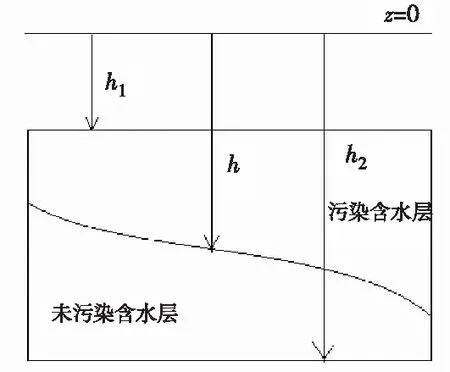
图1 水层结构示意图Fig.1 Structure of the water layer
1 主要数学结果
通过Darcy定律和质量守恒定律进行建模,可以得到一个强耦合抛物线方程组:
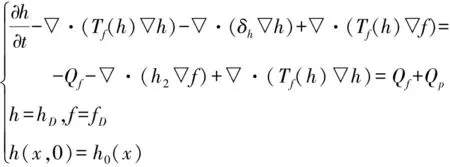
其中Tf(h)=h2-h,Tp(h)=h, ,δ 针对这个方程组,有如下存在性定理: (1) 使得h(0,·)=h0,0≤h(t,y)≤h2,∀(t,y)∈[0,T]×Ω。 首先介绍2个引理: 引理1[11]假设X是一个Hilbert空间,其中的元素f∈L2(0,T,X),使得∂tf∈L2(0,T,X′),有以下不等式: (2) 引理2[11]方程的解(hk,φ(hk))k∈N,满足以下不等式(3): φ(hk(·,t-ε))))dt≤C·ε,∀ε∈[0,T] (3) 存在性定理的证明如下: (4) 利用Schauder定理,证明∀T>0,k∈N,方程(4)都有解uk∈W(0,T),使得uk(0,·)=u0。首先固定k∈N,∀u∈V,则 所以,∀u=u(t)∈L2(0,T,V),有 另外,∀g∈H,u∈V,有 所以,可以得到∀g∈L2(0,T,V),存在惟一解u=:Ψ(g)∈W(0,T),满足 然后定义一个映射: Ψ:L2(0,T,H1(Ω))→L2(0,T,H1(Ω)) 其中(h,f)是方程组的解,显然所有这个映射的不动点都是式(1)的解,然后再证明这是一个从W(0,T)到W(0,T)的凸的、非空的、有界闭的映射,并且在W(0,T)上连续即可。 证明∀k,∀(t,x)∈[0,T]×Ω,都有0≤hk(t,x)≤h2;固定k≥0,η>0,假设uη(t,y):=((u+hD)(t,y)-η-h2)+,明显uη∈L2(0,T,V),并且▽uη=▽(u+hD)χ(u+hD>η+h2),然后假设w(t,y)=uη(t,y)χ(0,τ)(t),τ∈(0,T],代入方程式(1)中,再利用Mignot引理,其中假设f(λ):=(λ-η-h2)+,就可以证明∀τ∈[0,T],(u+hD)(τ,y)≤h2。 同理,可以证明∀τ∈[0,T],(u+hD)(τ,y)≥0。 证明数列{fk}k在L2(0,T,H1)中有界,这里主要利用Cauchy-Schwarz不等式、Gronwall不等式和Young不等式,通过分项积分,容易得到: 最后利用引理1和引理2证明所有序列{uk}k中的弱极限点u∈W(0,T)满足方程(4)。这样存在性定理就得证了。 针对长江水污染问题,利用Darcy定律和质量守恒定律,在污染水层和未污染水层为受限制含水层的假设下,同时假设它们之间的临界面光滑,建立一个强耦合抛物线方程和构造截断函数,利用Schauder定理,证明了该模型中临界面解的存在性,为研究水污染和治理提供了理论依据。
2 存在性定理的证明
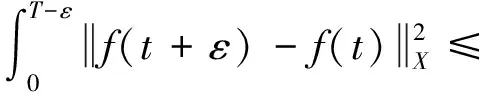

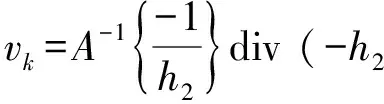
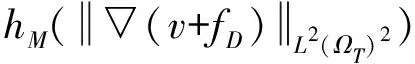
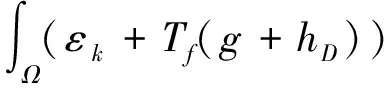
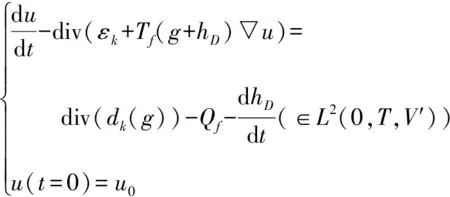
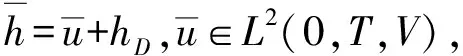
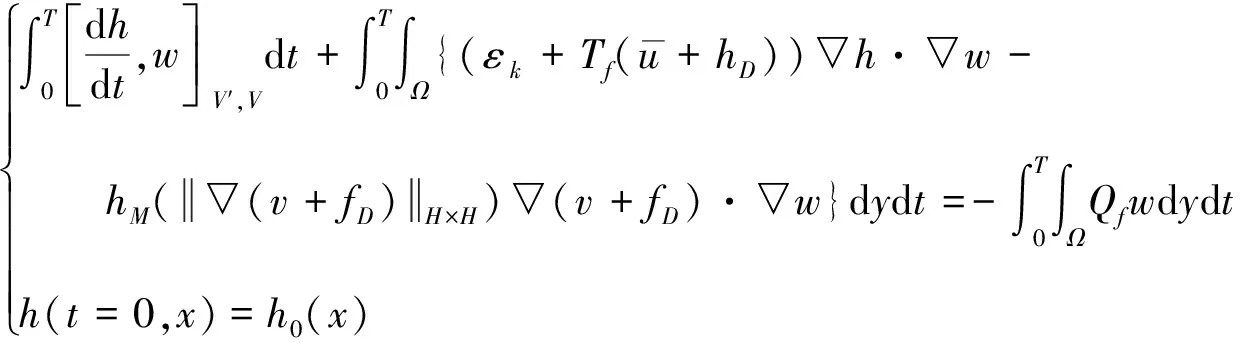
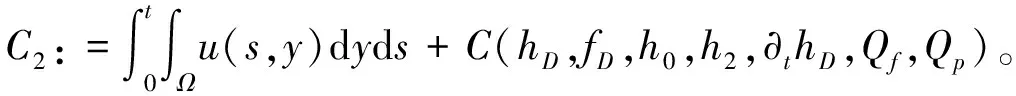
3 结 论
