张凤晓， 张丽平， 吴 涛，2

(1.安徽大学 数学科学学院，合肥 230601; 2.安徽大学 计算机智能与信号处理教育部重点实验室，合肥 230039)

0 引 言

模糊集概念[1—2]被提出后，被广泛应用于统计决策、系统工程、模式识别、人工智能等领域。Zadeh[3]在1975年提出二型模糊数用来解决不确定问题，但由于计算复杂，通常采用Mendel提出的区间二型模糊数[4]，区间二型模糊数是二型模糊数的特例。Zadeh[5]于2011年提出了Z-numbers的概念，Z-numbers的构造更好地考虑了信息的“可信赖”程度。Wang[6]根据Z-numbers和语言评价集，提出了语言Z-numbers，并定义了相关的一些算子。Xu[7]提出了不确定语言型变量，并基于语言型偏好关系提出了语言型变量的集结算子，这为语言型模糊数的决策提供了便利。Kang[8—9]等提出将Z-numbers转化为梯形模糊数来计算不确定问题，文献[10]将Z-numbers理论应用于关键缓存计算方法中。Bhanu[11]在Zadeh的基础上提出了一些Z-numbers的算子。Bao[12]提出了语言型集合的语言评估尺度，将语言型集合转化为具体的数值，为比较语言型模糊集之间的优劣性提供了有力的工具。Wang[13]和Peng[14]在前人研究的基础上，提出了新的语言型尺度函数，并运用在犹豫不确定语言型Z-numbers中，为语言型模糊集在实际决策应用做出了贡献。为了更好地表达现实环境中的不确定性，本文将区间二型模糊语言运用在Z-numbers中，以便更好地解决不确定问题。

提出了区间二型模糊语言Z-numbers(IT2FLZNs)在多属性群决策中的应用。首先，给出了关于区间二型模糊集及Z-numbers的相关概念，同时，提出了IT2FLZNs的定义，并给出了IT2FLZNs的相似度，利用相似度，构建数学模型求解各专家的权重及各属性的权重向量，并通过亲密度来确定折中方案。通过一个银行流动风险的实例，说明了方法的可行性与有效性。

1 基础知识

1.1 相关定义

定义1(二型模糊集[15]) 给定论域X及其元素x∈X，二型模糊集合A可以由其隶属函数μA(x,u)，μ∈Jx⊆[0,1]表示为

A={((x,u),μA(x,u)):∀x∈X,u∈Jx∈[0,1]}

(1)

其中，0≤μA(x,u)≤1，x是主变量，Jx是主隶属度值域，u是次变量，uA(x,u)是次隶属函数。

若论域X是连续的，则式(1)可以表示为

(2)

定义2 (区间二型模糊集[4]) 在二型模糊集中，当所有的μA(x,u)=1时，集合A为区间二型模糊集合，可表示为

(3)

为了方便，定义A=(AU,AL)，一个区间梯形二型模糊数记为

(4)

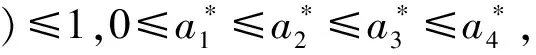
1.2 Z-numbers 模糊数

模糊集的创始人Zadeh 教授在经典模糊集的基础上，提出了Z-numbers 模糊集，与经典模糊集理论相比，Z-numbers 模糊集考虑了信息的可靠性程度，因而能更好地表达现实环境中的不确定性。

定义3( Z-numbers)[5]一个Z-numberZ是由一对有序的模糊数组成， 记为Z=(A,B)。A和B用来描述随机变量X的值，其中第一个元素A是对随机变量X的值的一个限制，第二个元素B表示的是对A可靠性程度的测量。例如，A和B用自然语言表示可为(好，可能)。

1.3 语言尺度函数

定义4(语言尺度函数)[16]假设si∈S是一个语言术语，其中S={si|i=0,1,2，…，2t}是语言型术语的集合。如果一个θi∈[0,1]是一个数值，语言尺度函数是从si到θi(i=0,1,…，2t)的一个映射f，被定义如下：

f:si→θi(i=0,1,…,2t)

(5)

并且， 0≤θ0<θ1<…≤θ2t≤1，所以θi可以看作是决策者对选择si的一种偏好，si越优则θi越大，偏好越强烈。

2 IT2FLZNs的运算及相似度计算

2.1 概 念

定义5(IT2FLZNs) 假设X是一个论域，A是一个区间二型模糊集合，B是一个包含奇数个离散有序语言型术语的集合，则在论域X上，一个区间二型模糊语言Z-number (IT2FLZN)可以表示如下：

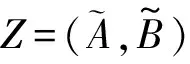
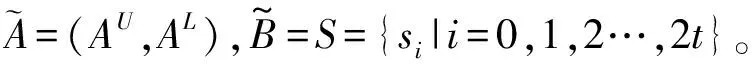
例1 假设t=3，A={非常低，低，中低，中，中高，高，非常高} 是一个区间二型模糊集合的语言集，B={极其不可能，非常不可能，不可能，偶尔，可能，非常可能，极其可能} 是对A可靠性测量的有序性语言集。则一个语言Z-number集合可表示为

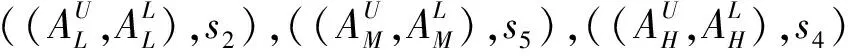
2.2 基本运算

定义6 假设Zi，Zj是两个区间二型模糊语言Z-numbers：

其中，sφi,sφj∈S={si|i=0,1,2，…,2t}，设f为一个语言尺度函数，λ>0，则IT2FLZNs运算如下：

(1) 加法运算。Zi⊕Zj=

(2) 减法运算。Zi-Zj=

(3) 乘法运算。Zi⊗Zj=

(4) 数乘运算。λZi=

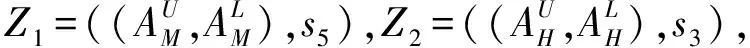
Z1⊕Z2=

Z1-Z2=

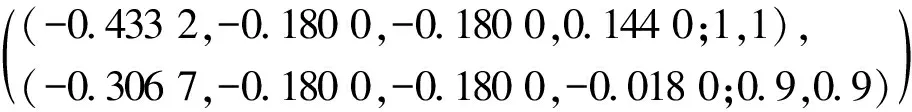
Z1⊗Z2=

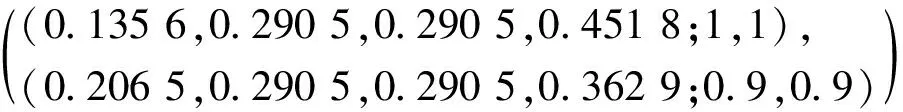
2Z1=

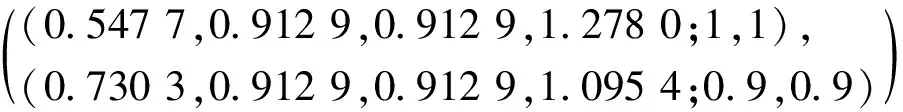
ZC=

2.3 相似度分析

定义7 (相似度) 设zi,zj是两个IT2FLZNs，其中：

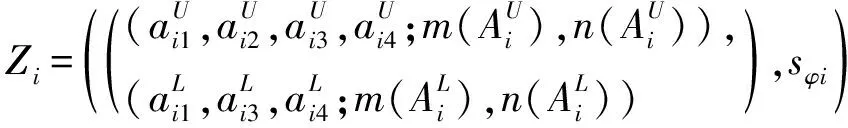
则zi,zj的相似度为

Sim(Zi,Zj)=1-d(Zi,Zj)

(6)

其中，

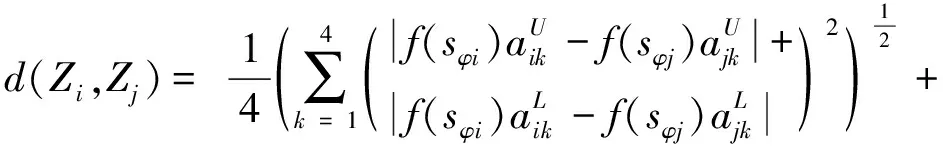
(7)

为zi,zj之间的距离，Sim(Zi,Zj)越大，则相似度越大。

性质1Sim(Zi,Zj)∈[0,1]

证明很显然，d(Zi,Zj)为欧氏距离，且d(Zi,Zj)∈[0,1]，所以性质1得证。

性质2Sim(Zi,Zj)=Sim(Zj,Zi)

证明由定义7本身得证。

性质3Sim(Zi,Zj)=1，当且仅当Zi=Zj。

证明充分性：如果Zi=Zj，则d(Zi,Zj)=0，所以Sim(Zi,Zj)=1。必要性：如果Sim(Zi,Zj)=1，则d(Zi,Zj)=0。由距离的定义可知Zi=Zj。

3 IT2FLZNs的多属性群决策方法

3.1 决策问题描述

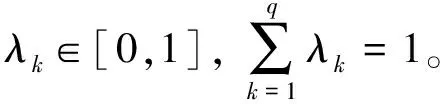
在群决策过程中，需要尊重每位专家的权威性，所以专家自身的权重需要考虑。由于相似度可以表示评估信息的相似性，所以当某一专家相似度矩阵值更大时，说明该专家与整体保持度高，差异性小，所给信息更重要，应该给该专家更大的权重，由此构建模型如下：

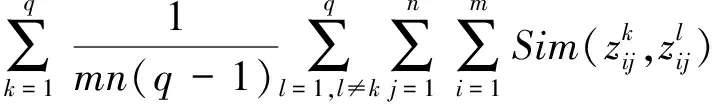
(8)

其中，Δ表示专家权重信息部分已知。

若在某一相同属性下，两个方案之间相似度很小，则属性扮演更重要的作用，应给与更大的权重，若相似度很大，则属性对方案选择影响不大，对应权重较小，由此，构建如下线性优化模型：

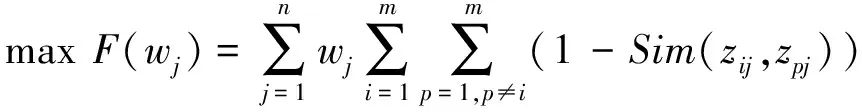
(9)

其中，Δ1表示属性权重信息部分已知。

3.2 决策步骤

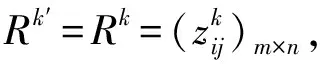
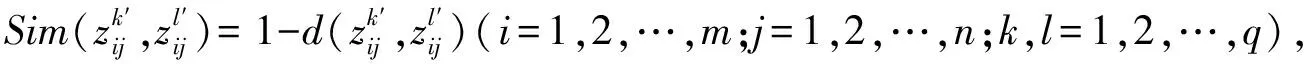
步骤3 通过式(8)计算专家的权重向量λ=(λ1,λ2,…λq)。

步骤4 根据专家的权重值，利用区间二型加权平均算子汇总群体决策矩阵R=(zij)m×n。

步骤5 通过式(9)计算每个属性的权重向量w=(w1,w2,…,wn)。

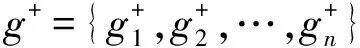
步骤7 计算各方案的群体效用值U(ai)、个体遗憾值R(ai)和亲密度Q(ai)，有:

(10)

(11)

(12)

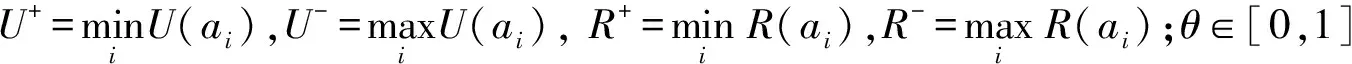
步骤8 分别根据U(ai)、R(ai)和Q(ai)对方案进行升序排列,得到3个排序,数值越小表明方案越优。

步骤9 确定折中方案。 设按照Q(ai)值升序的排列结果为a(1),a(2),…,a(m)。 如果a(1)同时满足以下两个条件,则a(1)为折中方案:

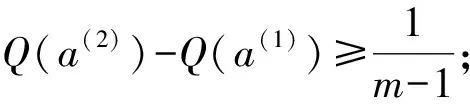
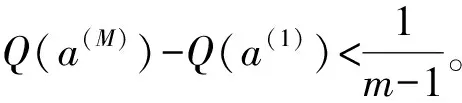
4 实例分析

流动风险对银行自身的稳定性十分重要，流动风险指的是银行在合同到期时无法按时、有效地满足其预期的合同支付义务，因此，银行的流动性能够持续保证其在技术上的偿付能力，而流动性风险评估对于世界各地的银行来说都是非常重要的。假设有3家银行A=(a1,a2,a3)将被评估，而在现实中会考虑4种属性:(c1)确保现金流入和现金流出之间的适当平衡的能力；(c2)协调银行发行短期、中期和长期融资的能力；(c3)优化再融资成本的能力，在流动性和盈利能力之间取得平衡；(c4)通过现金池技术或其他优化工具，优化银行结构为银行集团的能力。专家权重信息为Δ={0.1≤λ1≤0.4;0.15≤λ2≤0.35;0.2≤λ3≤0.35}，Δ1={0.1≤w1≤0.4;0.15≤w2≤0.35;0.2≤w3≤0.4;0.2≤w4≤0.3}，区间二型模糊集合所对应模糊数见文献[18]的表1，原始评估信息如表1—表3所示：

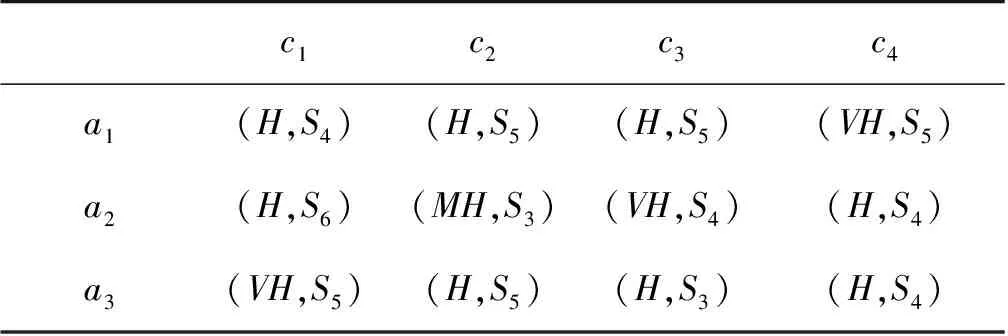
表1 专家d1决策矩阵Table 1 Expert d1 decision matrix

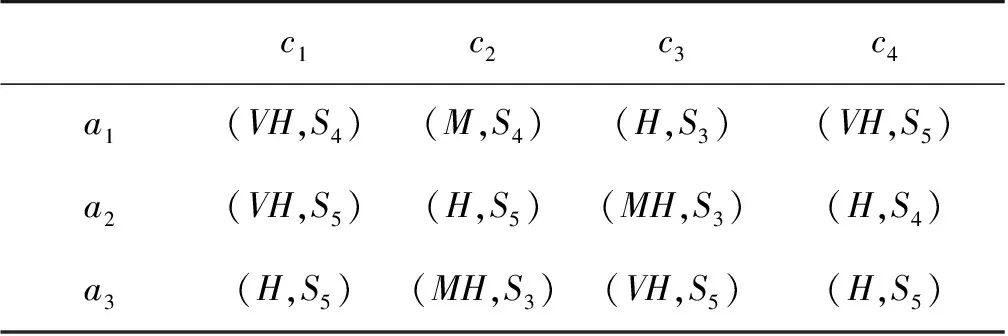
表2 专家d2决策矩阵Table 2 Expert d2 decision matrix

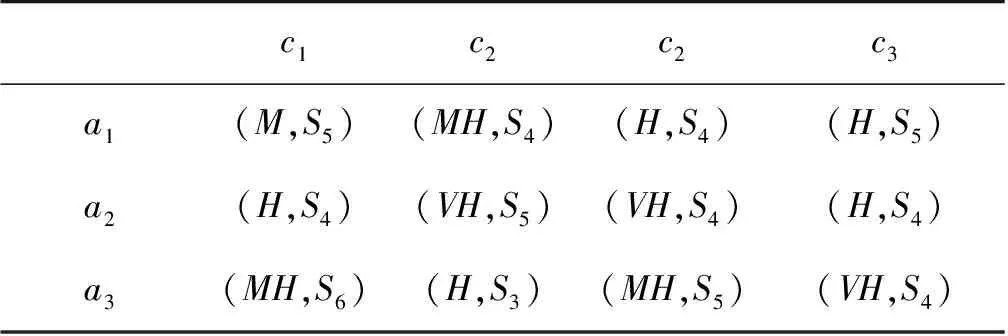
表3 专家d3决策矩阵Table 3 Expert d3 decision matrix

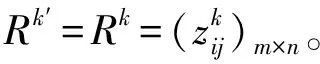
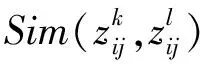
步骤3 通过模型式(8)，计算专家权重如下：

则专家权重为λ={0.3,0.35,0.35}。

步骤4 根据专家的权重值，可以利用区间二型加权平均算子汇总决策信息如下：

R=(zij)m×n：

z11={(0.588 4,0.729 9,0.729 9,0.818 3;1,1),(0.659 1,0.729 9,0.729 9,0.774 1;0.9,0.9)}
z12={(0.420 3,0.589 4,0.589 4,0.731 1;1,1),(0.504 9,0.589 4,0.589 4,0.660 3;0.9,0.9)}
z13={(0.527 2,0.709 1,0.709 1,0.827 5;1,1),(0.618 2,0.709 1,0.709 1,0.768 3;0.9,0.9)}
z14={(0.757 7,0.880 9,0.880 9,0.912 9;1,1),(0.819 3,0.880 9,0.880 9,0.896 9;0.9,0.9)}
z21={(0.697 6,0.846 7,0.846 7,0.905 3;1,1),(0.772 1,0.846 7,0.846 7,0.876 0;0.9,0.9)}
z22={(0.617 3,0.755 6,0.755 6,0.829 9;1,1),(0.686 4,0.755 6,0.755 6,0.792 7;0.9,0.9)}
z23={(0.601 4,0.704 0,0.704 0,0.753 5;1,1),(0.652 7,0.704 0,0.704 0,0.728 7;0.9,0.9)}z24={(0.571 5,0.734 8,0.734 8,0.816 5;1,1),(0.663 2,0.734 8,0.734 8,0.775 7;0.9,0.9)}
z31={(0.645 1,0.806 4,0.806 4,0.908 4;1,1),(0.725 8,0.806 4,0.806 4,0.857 4;0.9,0.9)}
z32={(0.488 7,0.642 5,0.642 5,0.744 1;1,1),(0.565 6,0.642 5,0.642 5,0.693 3;0.9,0.9)}
z33={(0.595 8,0.734 1,0.734 1,0.819 2;1,1),(0.664 9,0.734 1,0.734 1,0.776 6;0.9,0.9)}
z34={(0.652 3,0.793 8,0.793 8,0.850 2;1,1),(0.723 0,0.793 8,0.793 8,0.822 0;0.9,0.9)}

步骤5 通过模型式(9)，计算属性的权重为w=(0.15,0.35,0.2,0.3)。

步骤6 对群体决策矩阵R,确定方案正理想解g+={z21,z22,z33,z14}和负理想g-={z11,z12,z23,z24}。

步骤7 根据式(8)—式(10)计算各方案的群体效用值U(ai)、个体遗憾值R(ai)和亲密度Q(ai)，U(a1)=0.697 5,U(a2)=0.5,U(a3)=0.610 8；R(a1)=0.35，R(a2)=0.3，R(a3)=0.283 4。

根据式(10)，令θ=0.5，计算亲密度为Q(a1)=1，Q(a2)=0.124 6，Q(a1)=0.280 5。

步骤8 分别根据U(ai)、R(ai)和Q(ai)对方案进行升序排列,得到3个排序：

U(ai):a1≻a3≻a2
R(ai):a1≻a2≻a3
Q(ai):a1≻a3≻a2

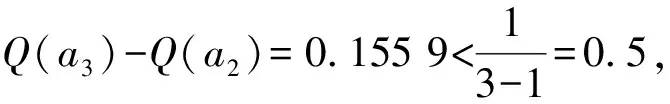
在实际决策中, 根据各专家不同的决策态度, 可以采取不同的偏好系数, 即θ可取 [0,1]的任何值。下面分析偏好系数θ的变化对最终排序结果的影响,计算结果如表4所示。

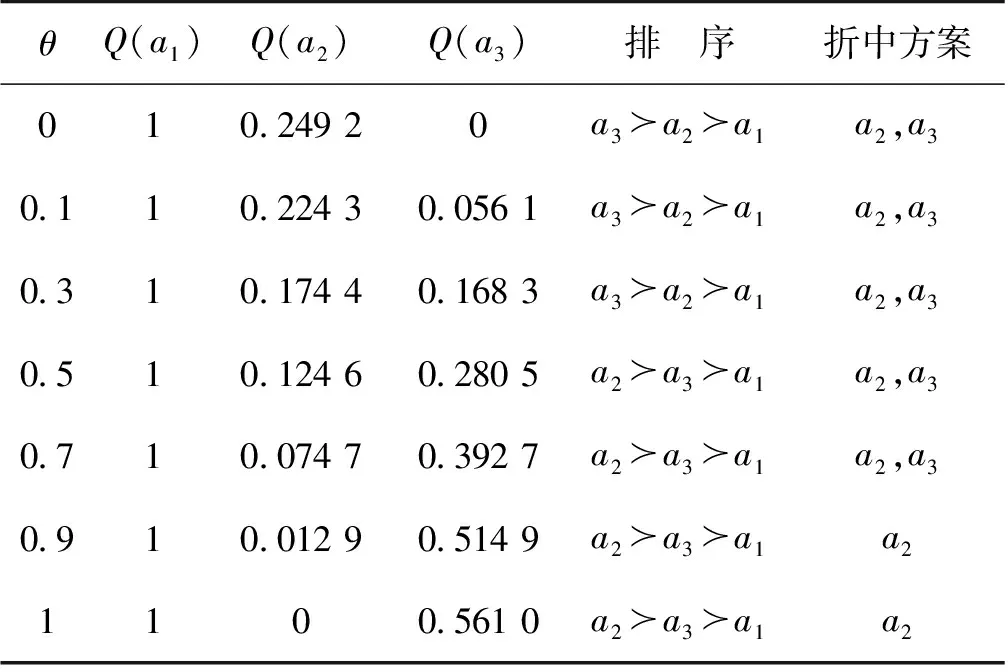
表4 偏好系数θ对排序的影响Table 4 Influence of preferece coefficient θ on sorting

显然, 从表4可以看出θ会对结果产生影响。当θ取值为[0,0.3] 即专家较多考虑个体遗憾时,折中方案为a2,a3；当θ取值为0.9 即较多考虑群体效用时，折中方案为a2。另外,当θ分别取两个极端值,即当θ=0，只考虑个体遗憾时,排序结果等价于依据个体遗憾最小R(ai)进行排序；当θ=1，即只考虑群体效用时，排序结果等价于依据群体效用最大U(a1)进行排序。

因此，θ描述了最大群体效用和最小个体遗憾之间的妥协，θ值的变化可以表达专家不同的主观偏好，提高决策的灵活性和可用性。

5 结束语

基于区间二型模糊集合在不确定问题中的广泛应用，以及Z-numbers对自然语言的客观信息和主观理解成分的并列表达，更好地考虑了信息的“可信赖”程度。由此，提出了区间二型模糊语言Z-numbers，并定义了相关算子，利用相似度，构建数学模型解决专家及属性权重，并通过群体效用值来确定折中方案。通过一个银行流动风险的实例，说明了该方法的可行性与有效性。下一步将考虑区间二型模糊集合与Z-numbers在决策中的其他应用。