Alice Medeiros Lima *,Wu Hong Kwong ,Antonio José Gonçalves Cruz

1 Chemical Engineering Graduate Program,Federal University of São Carlos,São Carlos,Brazil

2 Department of Chemical Engineering,Rod.Washington Luiz,Km 235-SP 310,São Carlos/SP,13565-905,Brazil

3 Department of Chemical Engineering,Federal University of São Carlos,São Carlos,Brazil

1.Introduction

The flexible tolerance method(FTM)is an extension of the Nelder–Mead method(or flexible polyhedron method,FPM)proposed by Paviani and Himmelblau[1].It transforms objective,equality,and inequality constraint functions(linear and/or nonlinear)in a problem of simple nonlinear optimization programming,with the same solution after introduction of the concepts of tolerance criterion,constraint violation,and near-feasibility.FTM can improve the value of the objective function by using information provided by feasible points as well as certain non-feasible points called near-feasible points[1].

The flexible tolerance method is a direct search deterministic optimization method,easy to implement and to use.However,its applicability and performance in process synthesis problems,and specifically in integration processes have not yet been analyzed.For this reason,much remains to be done concerning the development and/or improvement of the flexible tolerance method(FTM)to make it able to handle efficiently this type of problem.

In many nonlinear programming methods,a considerable amount of computational time is spent on satisfying rigorous feasibility requirements.FTM employs a tolerance criterion and an unconstrained nonlinear programming method for the constraint violation throughout the whole search,and thereby causes near-feasibility limits to become gradually more restrictive as the search proceeds toward the optimum solution,until at the limit only feasible vectors are accepted in the model.The Nelder–Mead flexible polyhedron method was proposed in order to perform the inner search without restrictions[1].

FTM has been used to solve nonlinear optimization problems with constraints in applications including multicomponent spectrophotometric analysis[2],determination of smooth time-optimal pathconstrained trajectories for robotic manipulators[3],an adaptive genetic algorithm to solve nonlinear multimodal and multi-constraint optimization problems[4],estimation of the kinetic parameters of an auto-catalytic reaction involving the pyrolysis ofn-eicosane[5],determination of an optimal sensing-system con figuration for a single object trajectory[6],and synthesis and analysis of processes with mass integration[7],amongst others.

Several difficulties have been noted using FTM in process synthesis problems by Limaet al.[7].The initial values used for algorithm initialization do not always converge to the optimal solution,when these initial values are distant from the optimal region,the search becomes slow or convergence is not achieved.Another problem is related to the parameter values of the Nelder–Mead method(for unconstrained searches).In the cases studied[7],the recommended values of these parameters were unable to provide the solution,so that it was necessary to adopt a trial and error procedure until values were found for which FTM achieved convergence.

Some of these difficulties were overcome as reported by Limaet al.[8]using scaling of variables and hybridization with different unconstrained methods(modified Powell's method,BFGS and PSO).The best results reported were obtained using scaling variables(FTMS)and using the PSO method during initialization(FTMS-PSO).

In light of the earlier findings,the aim of the present work was to analyze the performance of FTMS and FTMS-PSO coupled with the adaptive Nelder–Mead simplex algorithm and barrier.A description is first provided of the standard flexible tolerance method(FTM)and the modifications included in order to improve its performance.The ability of the proposed method to resolve a number of standard nonlinear constrained test problems is then presented.

2.The Flexible Tolerance Method and Proposed Modifications

2.1.The flexible tolerance method

The general nonlinear programming problem can be stated by Eqs.(1)–(3):

wheref(x)is the objective function,hi(x)the equality constraints andgi(x)the inequality constraints.

The strategy of FTM is to combine all the constraints into a single inequality constraint,with the violation of this constraint then being permitted within a decreasing tolerance.A general unconstrained minimization algorithm can be applied for the solution of the overall inequality constraint.The functional of the equality and inequality constraints of Eqs.(1)–(3)is represented by Eq.(4).

The general nonlinear programming problem can then be rewritten(Eqs.(6)and(7)).

where Φ(k)is the flexible tolerance criterion for feasibility in thekstage of the search.

In a previous work[8]the unconstrained search was performed using the modified Powell's method and the BFGS method.As pointed out by the authors,these methods do not outperform the Nelder–Mead method during the minimization of constraints.In this work,the unconstrained search was performed by the Nelder–Mead method,so can be described by Eq.(8).

Φ(k)behaves as a positive decreasing function of x.The vector x(k)(representing a vertex of the polyhedron)may be classified(for a given value of Φ(k))as:(a)feasible,ifT(x(k))=0;(b)near-feasible,if 0＜T(x(k))≤Φ(k),and(c)non-feasible,ifT(x(k))＞Φ(k).In eachkth step of the search,Φ(k)is set equivalent to the smallest value of Φ(k−1),the tolerance criterion also collapses,and at the limit,will get zero(Eq.(9)).

where x*is the solution vector,within tolerance ε.

FTM uses two searches to satisfy the feasibility constraint.The outer search,detailed in Fig.1,is a variation of the Nelder–Mead method that minimizes the objective functionf(x).The inner search,detailed in Fig.2,minimizes the value ofT(x).In the outer search,when a new vertex is found,its feasibility is assessed.If the vertex is near-feasible,the search follows the procedure of the Nelder–Mead method.If,on the other hand,the outer search selects a non-feasible vertex,the inner search converts it into a near-feasible vertex.The inner search starts from the non-feasible vertex and applies the Nelder–Mead method to search through the constraint space until a vector is found that satis fies the condition of feasibility or near-feasibility.

The FTM terminates in one of two ways:(a)Φ(k)≤ε,the search has been successful,or(b)a feasible or near-feasible vertex cannot be found by inner searching and the search must be restarted with a different initial vertex,x(0).

As reported by Limaetal.[8]the flexible tolerance method with scaling of variables(FTMS)and hybridized with PSO(FTMS-PSO)was a powerful strategy to improve FTM performance.Thus,the FTMS and FTMS-PSO was employed in this work to try new modifications and possible improvements.

2.2.The Nelder–Mead method

The Nelder–Mead method,also known as the flexible polyhedron method(FPM),is an unconstrained search method that was used in this work to perform the unconstrained searches in the FTM,as proposed by Himmelblau[9].The FPM minimizes a function ofnindependent variables using(n+1)vertices of a flexible polyhedron in ℜn.The FPM starts with a set of(n+1)vectors that represent the vertices of a regular simplex,described by matrix D,in which the columns represent the components of the vertices and the rows represent the coordinates(Eq.(10)).

whered1andd2are described by Eqs.(11)and(12),respectively,andtis the distance between two vertices.

The flexibility of the polyhedron enables efficient searching and the avoidance of difficulties in the normal simplex procedure when the search encounters curving valleys or curving ridges in the search space.Improved objective function values are found by successively replacing the point with the highest value off(x)by better points,until the minimumf(x)is found.A pseudocode of the Nelder–Mead method or FPM is shown in Algorithm 1.

Algorithm 1.Pseudocode of Nelder–Mead method or FPM

2.3.Adaptive parameters of the Nelder–Mead method

In the standard implementation of the FPM or Nelder–Mead method,the parameters of reflection(α),expansion(γ),contraction(β),and reduction(δ)assume the values presented in Eq.(13).

It has been found previously that the FPM algorithm becomes inefficient in high dimensions([10,7]).In order to improve the performance of the FTM,the adaptive parameters suggested by Gao and Han[10]were used in this work.According to the authors,these can reduce the chances of using reflection steps,while avoidance of rapid reduction in the simplex diameter should help to improve the performance of the FPM(and in this case also the FTM)for large dimensional problems.The coefficients are described in Eq.(14).

2.4.Modified flexible tolerance method proposed(MFTMS)

During the optimization process,the flexible tolerance method can found some vertices of polyhedron outside the limits of variables.This occur due to the fact that the steps of reflection,expansion,contraction and reduction do not use the range of variable to perform their operations.Then,considering the scaled problem,the vertices sometimes exceed the upper bound(+1.0)or the lower bound(−1.0).This behavior cause the degeneration of the polyhedron and difficult the constraints minimization,since some vertices is outside the feasible search region.The proposed modification limits the variables that exceed the variation range in any of the optimization steps into the scaled interval,acting as a barrier,as indicated in Eq.(15).

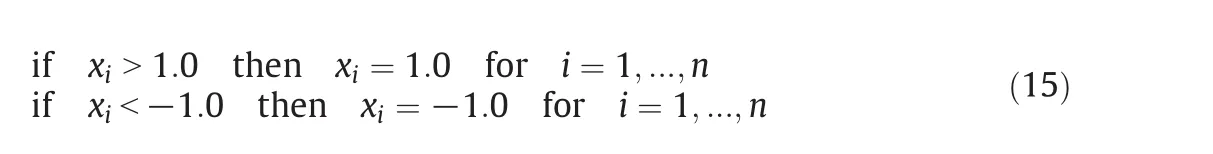
2.5.Hybridization of the modified flexible tolerance method proposed with PSO(MFTMS-PSO)

The method proposed in the previous section was hybridized with the PSO method.The same strategy reported previously[8]will be employed in this work.The PSO acts in the initialization of the search to find a net of values feasible,and then the MFTMS is applied to best particle.

3.Application in Test Problems

The FTM and the proposed modifications were applied to a set of functions of G-Suite from Lianget al.[11],presented in the Congress of Evolutionary Computation in 2006,in order to evaluate their performance.The methods with the best performance in this benchmark were applied to solve mass integration problems.These set of functions,which cover a wide range of nonlinear constrained optimization problems,with real problems and some generated problems,and different constraint types(physical,time,geometric,etc.),have been used previously to validate optimization algorithms and compare their performance([12,13,8]).The functions are described in detail by Lianget al.[11]and a brief problem description are reported in Limaet al.[8].

Fig.1.FTM algorithm flowchart for performing the outer search that minimizes the objective function f(x).All vectors x are assumed to represent x(k),unless noted otherwise.Adapted and modified from Naish[6].The gray boxes indicated the inner search performed by Nelder–Mead.

The FTM/FTMS and modifications were implemented in Python™,and the optimization calculations were performed using Eclipse IDE software,run under a Linux-like operating system installed on a 2 GHz Pentium(R)dual-core computer.

The performance of the FTM and the modified algorithms obtained in a previous work[8]FTMS and FTMS-PSO was compared with the different methods proposed in this work:

•FTMA:The flexible tolerance method(FTM)using adaptive parameters of the Nelder–Mead method(FPM)

•FTMAS:The flexible tolerance method with scaling(FTMS)and with adaptive FPM parameters

•MFTMS:The FTMS including the barrier modification

•MFTMS-PSO:The FTMS-PSO[8]including the barrier modification.This code was run 20 times,and the best and worst results were reported.

The problems were grouped into two sets:(a)problems of small dimensions(2≤n≤6),and(b)larger problems(n＞6).In all cases it was adopted a tolerance of ε=10−5,and the size of the initial polyhedron wast=0.4.

Based on the results found for the test problems of G-Suite previously described,it was applied the best methods to solve specific engineering problems,namely mass integration problems.

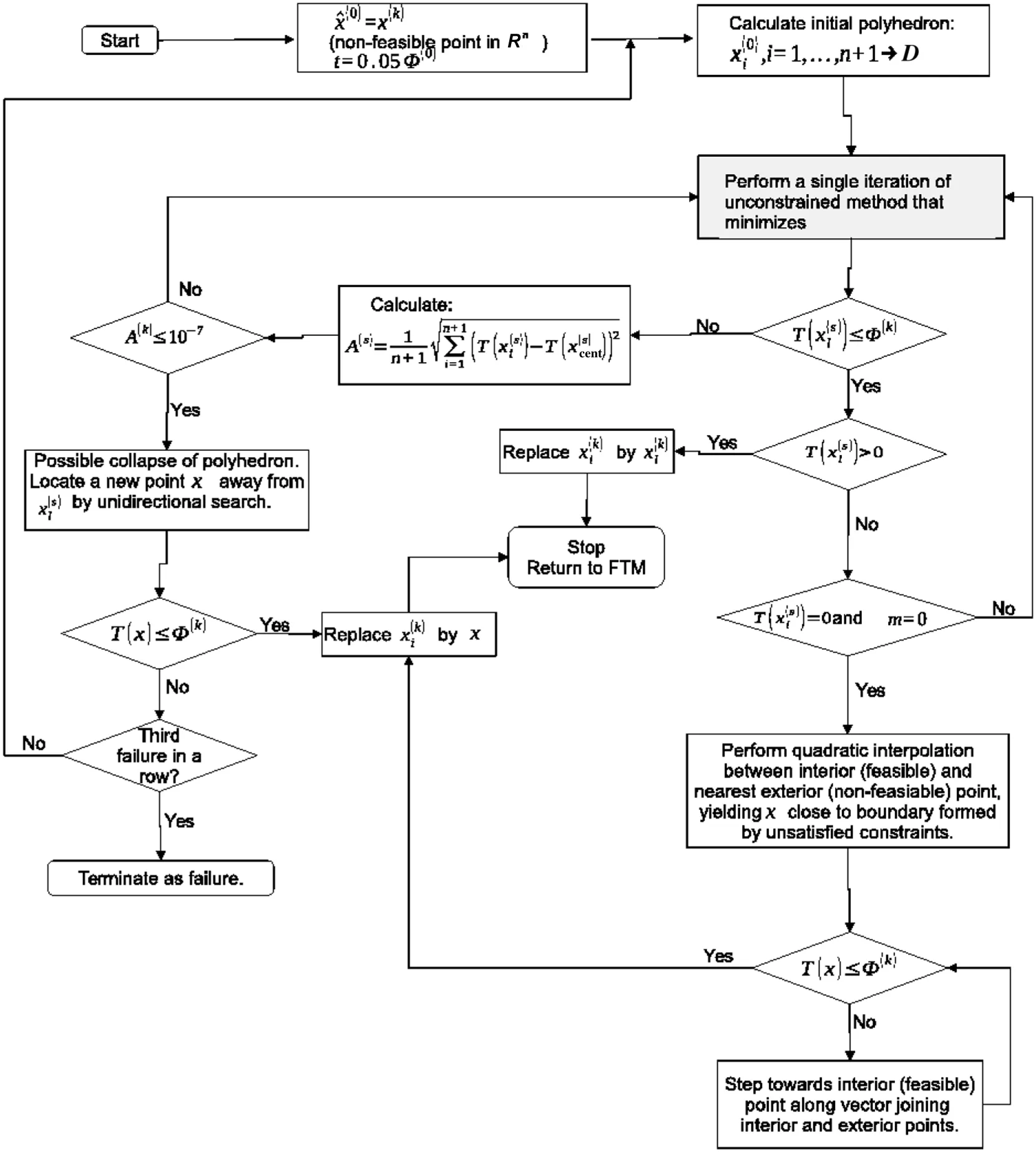
Fig.2.FPM algorithm flowchart.All vectors x are assumed to represent x(k),unless noted otherwise.Adapted and modified from Naish[6].

4.Results

In order to visualize the trajectory of the algorithms proposed in this work,a simple problem will be used for comparison.This same problem was used in a previous work[8].Fig.3 shows the objective function,the equality and inequality constraints and the optimum point.

Table 1 shows the number of objective function evaluations,the number of iterations and the processing time(using the machine described previously)for the four optimization methods implemented in this work.The optimum value for this problem was x*=[0.823 0.911]Twhen the objective function assumed the value off(x)*=1.393.

Fig.4 shows the trajectory of each method from the initial(nearfeasible)point until the convergence to the optimum point.The initial nonfeasible point was x(0)=[2 2]Twith objective function value off(x)(0)=1.0 for FTMA,FTMAS and MFTMS methods.The MFTMS-PSO method generated the initial point randomly,and the MFTMS started in the best particle founded after 100 generations,that is x(0)=[1.267 0.791],with the objective function value off(x)(0)=0.581.

As can be observed in Table 1,the algorithms tested were able to find the optimum point for this simple problem.Comparing the number of objective function evaluations and iterations,the FTMA and the FTMAS methods presented the worst performance,with the largest values.The best performance were presented by the MFTMS and MFTMS-PSO methods.The MFTMS showed the shortest processing time and the low numbers of iterations and objective function evaluations.For the MFTMS-PSO method,the processing time was longer,due to the time consumed by the initialization step with the PSO method,however presented the lower number of iterations and evaluations of objective function similar to MFTMS.The trajectories followed by each method(Fig.4)indicated that MFTMS had a more direct path than the other methods.

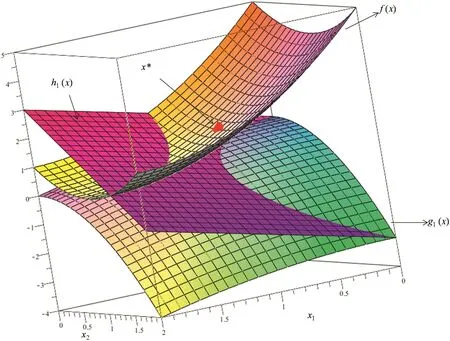
Fig.3.Objective function(f(x)),equality constraint(h1(x)),inequality constraint(g1(x))and optimum point(x*)for the test problem of Eq.(16).From Lima et al.[8].

Table 1Results summary for the test problem described in Eq.(16)

4.1.Problems of small dimensions(2≤n≤6)

Table 2 shows the objective function values for problems of small dimensions.The MFTMS and MFTMS-PSO codes showed the best performance in reaching the optimum.Table 3 summarizes the number of objective function evaluations required for FTMA,FTMAS,MFTMS and MFTMS-PSO for problems of small dimensions(2≤n≤6).

The adaptive parameter strategies(FTMA and FTMAS)showed poor performance compared to the other techniques(MFTMS and MFTMSPSO),and required a significantly greater number of objective function evaluations in the cases where convergence was achieved.This was also noted by Gao and Han[10]for problems with small dimensions.In almost all cases,convergence was not achieved using adaptive parameters.

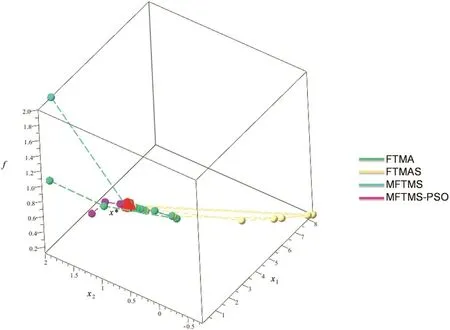
Fig.4.Trajectories from the nonfe asible initial vector obtained using the different optimization methods for test problem(Eq.(16)).

FTMA was unable to reach the known optimum for the g08 function,despite the greater number of objective function evaluations compared to the other codes.

The feasible region of the search for problem g12 consisted of 93=729 disjointed spheres.The ability of the methods to deal with multiple disjointed regions was poor,as can be observed from the objective function values found by MFTMS and MFTMS-PSO.This results agree with the ones reported previously[8].

The MFTMS and MFTMS-PSO showed similar performance to the codes without the barrier(FTMS and FTMS-PSO)reported by Limaet al.[8].

The problem g05,that comprises difficult equality constraints,the MFTMS was able to reach the known optima in a smaller number of objective function evaluation and iterations(10658[1013])compared with the results reported by FTMS(36019[1531])[8].

Solution of problem g16,that present complex objective function and a large number of nonlinear constraints,was difficult to be obtained even with indirect method,as GRG,that failed to solve it[9].The MFTMS code reached convergence with a smaller number of objective function evaluations(284[146])when compared with the FTMS(369[146])[8].The method hybridized with PSO,MFTMS-PSO,also achieved convergence(395[225])whereas FTMS-PSO did not converge[8].

4.2.Larger problems(n＞6)

Table 4 summarizes the objective function values obtained for large problems,which showed a greater number of constraints than the preceding group.MFTMS and MFTMS-PSO achieved successful convergence,with MFTMS generally giving better results than MFTMS-PSO,and the use of adaptive coefficients did not improve the performance of FTMS or FTM.

The numbers of objective function evaluations for larger problems(n＞6)are illustrated in Table 5.The adaptive strategy was ineffective for use with this group of problems,since few convergences were achieved with FTMA and FTMAS.However,barrier proved to be a useful strategy,with the number of function evaluations required for FTM and FTMS being similar to the ones reported previously[8].

The problem g19 as pointed out previously[8]presents a large number of local optima.MFTMS-PSO presented a good performance reaching the known optima in similar number of objective function evaluations and iterations than FTMS-PSO[8].This problem represents a challenge for any direct method of optimization(since they are more prone to be stuck in a local optimum),and the hybridization of MFTMS with PSO also proved to be efficient to overcome this awkwardness.

Problem g20 is sufficiently complex to provide a challenge for any nonlinear programming algorithm.Despite this,MFTMS and MFTMSPSO were able to converge to optima reported in literature[9].MFTMS and MFTMS-PSO required a lesser number of objective function evaluations and iterations when compared with the corresponding codes without barrier[8].

It has been reported previously by Gao and Han[10],that the use of adaptive parameters in the Nelder–Mead method can outperform the standard implementation for high dimensional problems.Nonetheless,in the present case the combination of adaptive parameters with flexible tolerance did not prove to be efficient,although reasonable results were obtained in a few cases(such as g09).

This set of functions was evaluated in CEC2006 using different evolutionary algorithms as evolution strategies,evolutionary programming,differential evolution,particle swarm optimization and genetic algorithms[14].The advantage of MFTMS in comparison with the stochasticmethod is the possibility of prediction of all steps knowing the start point,that is,it always takes up the same response from the same starting point.Since using the MFTMS is unnecessarily performing various runs and choice algorithm parameters that can change for a specific problem.Furthermore,the number of objective function evaluation was smaller than values reported[14],which was set in 5000,50000 and 500000 evaluations.

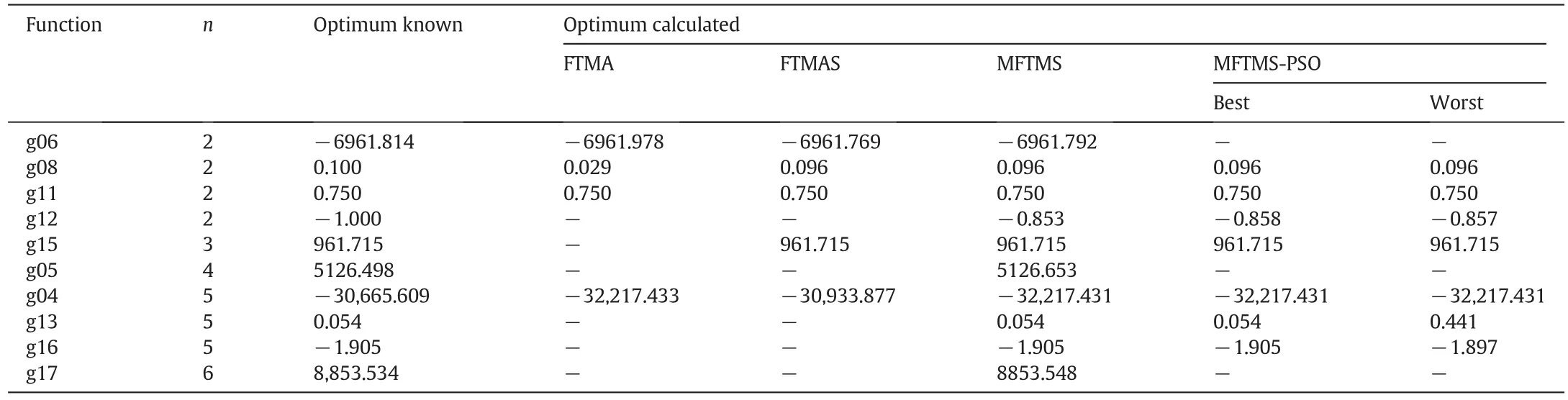
Table 2Objective function values for problems of small dimensions(2≤n≤6)

Table 3Number of objective function evaluation and iterations(in[])for problems of small dimensions(2≤n≤6)

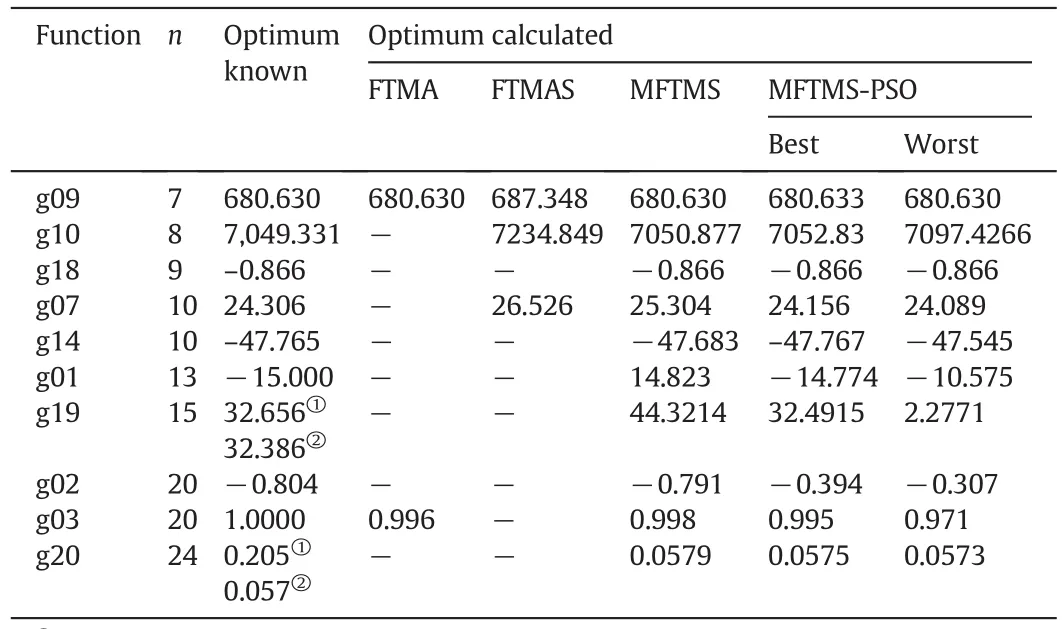
Table 4Objective function values for problems of large dimensions(n＞6)

However,the use of stochastic method PSO together with MFTMS proved to be an efficient strategy in problems that present many local optima or even when the starting point used does not reach convergence.This hybrid method can also corroborate to find global optima in nonlinear constrained optimization,which the global optimum cannot be guaranteed[15].

Table 5Number of objective function evaluations and iterations(in[])for problems of large dimensions(n＞6)

4.3.Mass integration problems

FTM was applied by Limaet al.[7]to solve mass integration problems.According to the authors the method presented some difficulties during the search process.Some of these difficulties were regarding to the unable capacity in reach the optimal process con figuration from the current process situation,probably due the current process situation be a local optimal point.In this paper three mass integration problems were solved using the MFTMS method proposed in this work,and FTMS-PSO reported previously[8].

Mass integration problems are typically complex problems since the optimization needs to consider a large number of equality constraints,and the variables generally have different ranges(as composition,temperature,pressure and others),which make the search process in the viable space difficult.The equality constraints are related with mass and energy balances,process equations and thermodynamic.The inequality constraints refer to environment issues(the pollutant level needs be less than a certain value),technical(temperature,pressure and/or flow rate cannot exceed determined value),and thermodynamic(positive values of driving force in transport process of mass and energy).

One of the possible mass integration formulation allows the identification of the minimum cost(or mass flow)of fresh streams,the best allocation of the process sources(streams that carry the species)to the sinks(units that can accept the species),and residual disposal.The representation of this problem is shown in Fig.5.The nonlinearities are due,mainly,to the fact that the constraints from the mass balance of the components are bilinear in relation to flow and concentration,and to process model equations(when used),which are generally nonlinear.The problem may be expressed as follows for a given process:

Fig.5.Superstructure used in NLP formulation representing the source-sink allocation.Adapted from El-Halwagi[16].

in whichzjminandzjmaxare the minimum and maximum allowed composition at unityj.

•A net of process sources:Sources={i=1,2,...,Nsources}that can be recycled/reused in the process sinks.Each source has a mass flowrate,Wi,and a composition,yi.

•A net of fresh sources(or news):Fresh={r=1,2,...,Nfresh}that can be bought to supplement the use of the process sources in the sink process.The cost of fresh sourcerth is represented byCr(USD·kg−1),its composition byxrand the flowrate byFr.

The optimization problem formulation is given by Eqs.(18)–(26).The objective function may be the minimization of the cost of fresh sources(Eq.(18))or minimization of mass flow of fresh sources(Eq.(19)).

The constraints of such modeling are:

•Each source,i,is divided intoNsinksfractions that can be allocated in several sinks(Fig.6).The flow of each fraction iswi,j;and one of these fractions is directed to the waste(wi,waste),this stream can be sent to waste treatment plant,or it can be a non-recycling material stream in the original waste sink.Similarly,each fresh source is divided intoNsinksthat are allocated to the various sinks(fr,j).

Fig.6.Sources division.Adapted from El-Halwagi[16].

Therefore,the constraint corresponding to the division of the process sources is:

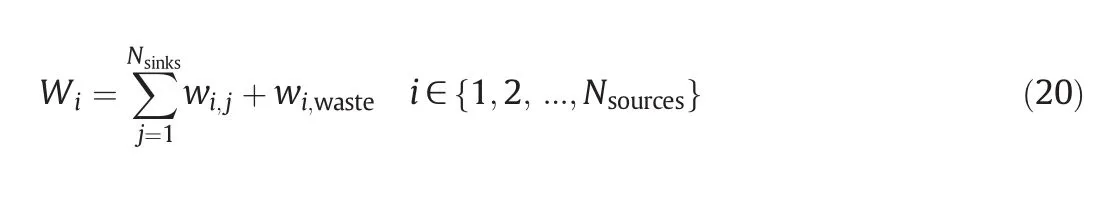
Thus,a similar constraint corresponding to the division of fresh sources:•

Then,it is analyzed the opportunities of mixing these fractions and their allocation to the sinks(Fig.7).The constraints related to the mixture into the sinkjth are described in Eqs.(23)–(24):

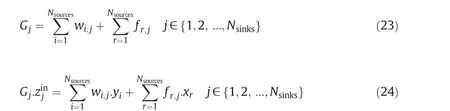
Fig.7.Mixture of the fractions of process sources and fresh,and sinks allocation.Adapted from El-Halwagi[16].

•To ensure non-negativity in the fresh streams and in the fractions of the sources allocated to the sinks,the constraints of Eqs.(25)and(26)are added:

In this model,constraints related to the process model,the cost of pipes,etc.,can still be included.Further details on mathematical formulation of mass integration can be found in El-Halwagi[16]and El-Halwagi[17].

Thus,solving this type of problem using a direct algorithm as FTM with or without modifications is a challenge.The capacity of FTM to deal with this problem was previously investigated[7].Based on these results some modifications(previously discussed)and reported by Limaet al.[8]were proposed and tested in the benchmark problems of G-Suite.The method that presents best performance in this work was MFTMS.The hybridized method MFTMS-PSO presented similar performance to the FTMS-PSO reported previously in Limaet al.[8].However,FTMS-PSO fits better to the optimum known,thus this method will be used to solve mass integration problems.

Since this type of problems was difficult to solve using the direct optimization method FTM,in this work,the problems were reformulated using the explicit substitution method.This strategy was used to diminishing the number of variables to be evaluated in the MFTMS and FTMS-PSO.Then,the polyhedron constructed during the search of optimum decreases and the algorithm becomes more efficient.

The proposed methods overcome the shortcomings of the original FTM method for mass integration problems,as can be readily seen in the results below.The MFTMS was able to find the optimum process con figuration from the current process con figuration.In FTMS-PSO method,the initialization with PSO proved to be advantageous to solve this kind of problem,since a starting point is not required.Due to the generation of different starting points in each execution,FTMSPSO corroborates the convergence to global optimum.These results were possible due to the modifications proposed.The particle swarm method(PSO)allowed a better exploitation of the search region,which helped the deterministic method FTMS to conduct the search in the optimum direction.The barrier introduced in FTMS,which resulted in the MFTMS method,prevented the polyhedron degeneration that was observed in the original FTM method when solving mass integration problems[7].

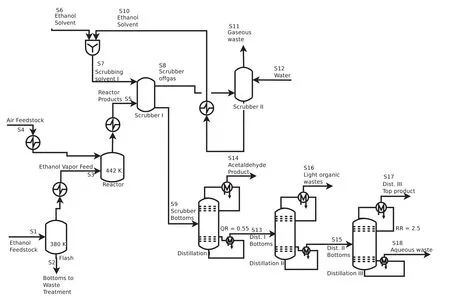
Fig.8.Flowsheet of acetaldehyde production by ethanol oxidation,Problem 1.From Lima et al.[7].

4.3.1.Problem 1—maximize the overall process yield

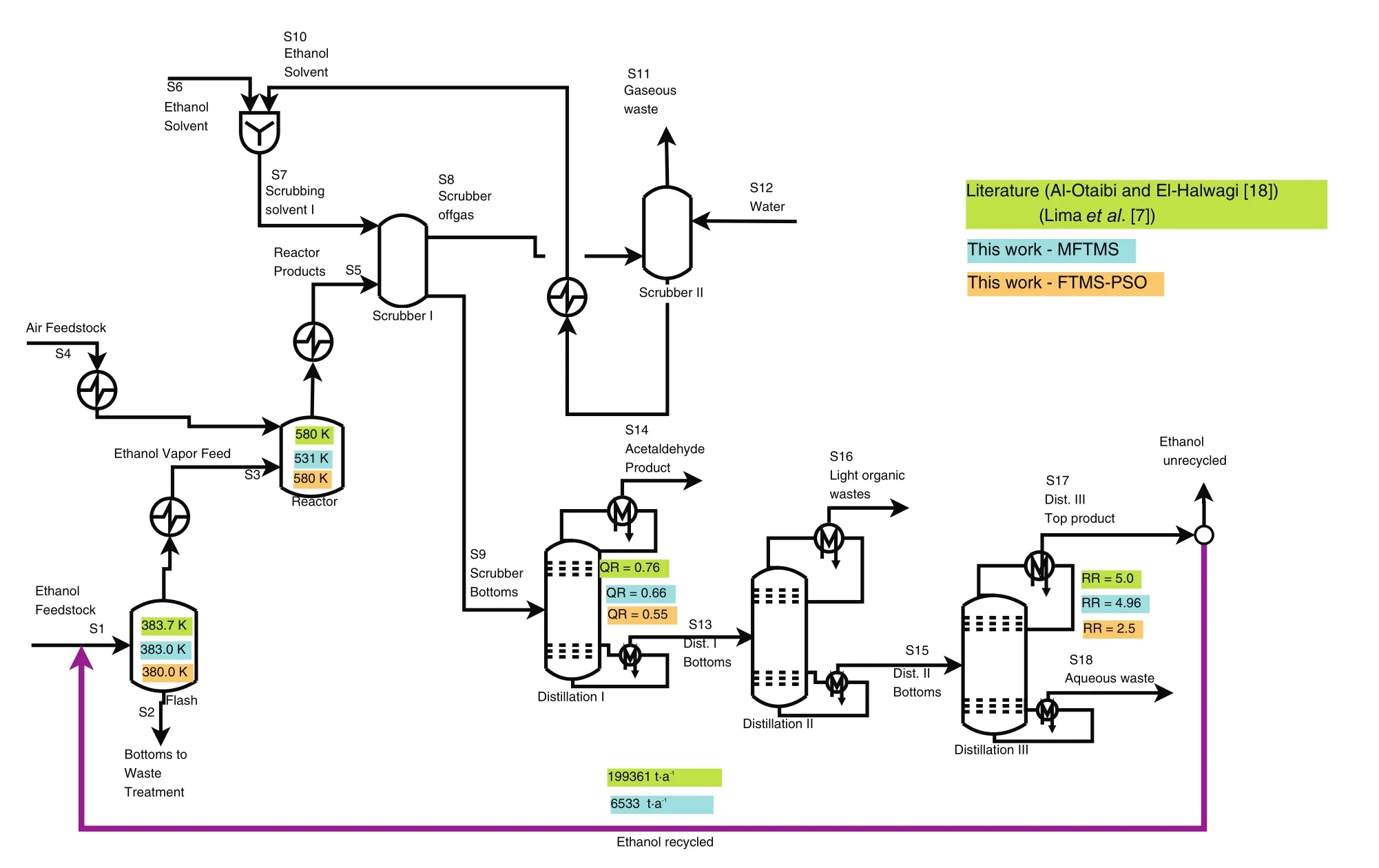
Fig.9.Optimized process flowsheet of acetaldehyde production by ethanol oxidation,Problem 1.

This problem deals with yield targeting in acetaldehyde production by ethanol oxidation([18,7]).The process flowsheet is shown in Fig.8.The objective was to maximize the overall process yield(YP)without adding a new process equipment,although process modification and direct recycle.Direct recycle was only allowed from the top of the third distillation column to the flash column.This mass integration problem present a superstructure source-sink(nonlinear programming)with process model in its constraints.The equality constraints include mass balance,constitutive equations for ethanol recovery,reaction yields,source-sink allocation,and inequality constraints related to limits of operation(temperature,re flux ratio,etc).The original formulation presents 31 variables,23 equality constraints and 36 inequality constraints,and the mathematical formulation is reported by Al-Otaibi and El-Halwagi[18].After applying explicit substitution method 21 variables were made explicit,and the resulting problem present 9 variables,2 equality constraints and 19 inequality constraints.

The results founded by the different methods indicated that the yield process improvement can be achieve with different plant con figurations.The optimized process flowsheet is shown in Fig.9,and the main optimized parameters are shown in Table 6.

In the previous work[7]the FTMin its standard formulation demonstrated be able to found the optima(not starting the search from the current process point).However,using MFTMS the optimum point was reach starting the search at the current process con figuration,despite the large number of objective function evaluations(2127)and 804 iterations.The optimum agree with the ones reported previously([18,7]),however the operational parameters are different(see Fig.9 and Table 6).

The results found by FTMS-PSO showed a con figuration that none ethanol is recycled to the flash,the process parameters are maintained and the increase in yield process is obtained through manipulation of fresh ethanol fed to the flash(S1 stream).These solutions obtained through direct optimization MFTMS method and the hybrid method FTMS-PSO may represent a local optimum.

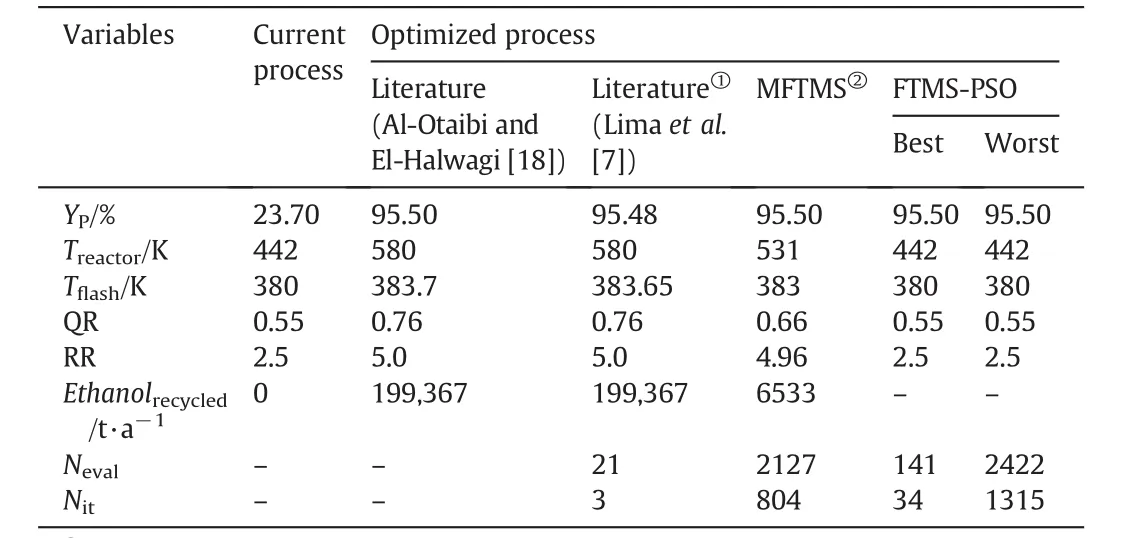
Table 6Main results for Problem 1.N it:number of iterations,N eval:number of objective function evaluations

4.3.2.Problem 2—minimization of the total load of a toxic pollutant discharged into terminal plant wastewater

This problem deals with minimization of the total load of a toxic pollutant discharged into terminal plant wastewater,using segregation,mixing and recycle strategies.The process refers to the production of ethyl chloride by catalytic reaction between ethanol and hydrochloric acid[17].The process diagram is indicated in Fig.10.The optimization problem in this process model includes source-sink representation(Fig.11)to allow consideration of segregation,mixing,and direct recycle strategies,and the material balance of water and chloroethanol.A detailed description of process can be found in El-Halwagi[17].(See Figs.12 and 13.)

The original problem formulation present 30 variables,19 equality constraints and 32 inequality constraints.After explicit 16 variables,the problem has 14 variables,3 equality constraints and 22 inequality constraints.The main parameters optimized are showed in Table 7.

As mentioned for the Problem 1,the use of FTM in this case also was not able to reach the optimum from the current process situation as reported by Limaet al.[7].Despite the large number of objective function evaluations,applying MFTMS and FTMS-PSO the optimum point was found and agree with the one reported by El-Halwagi[17],and leave to the con figuration of optimized process shown in Fig.14,the main variables values are shown in Table 7.The results shown in this paper differ from the results found in a previous work[7]for this problem using FTM without modifications(when the solution could be prone to a local optimum).

Fig.10.Flowsheet of the production of ethyl chloride,Problem 2.Adapted from Lima et al.[7].

Fig.11.Source-sink representation of Problem 2.Adapted from Lima et al.[7].

4.3.3.Problem 3—production of phenol from cumene hydroperoxide

The objective of this problem is determining the targets for minimum consumption of freshwater,minimum wastewater discharge and minimum operational cost(including freshwater and piping cost).The complete process description can be found in Hortua[19].The process flowsheet and the source-sink representation are shown in the Figs.10 and 15,respectively.

The original problem formulation has 27 variables,15 equality constraints and 30 inequality constraints.After explicit 14 variables,the problem has 13 variables,1 equality constraint and 19 inequality constraints.From the current process con figuration,the MFTMS and FTMS-PSO reach the optimum con figuration considering mass integration issues(Table 8).The total cost found was 41815.91 USD·a−1,with the minimum consumption of freshwater of 2084.26 kg·h−1and a minimum target for waste discharge of 3161.23 kg·h−1,this values agree with the reported by Hortua[19].The process flowsheet optimized with the recycle is shown in Fig.14.

Fig.12.Optimized process flowsheet of the production of ethyl chloride,Problem 2.

Fig.13.Flowsheet of the production of phenol from cumene hydroperoxide,Problem 3.Adapted from Hortua[19].

5.Conclusions

This paper proposes the use of adaptive parameters in the flexible tolerance method(FTMA)and in the FTMS previously reported[8](FTMAS).An improvement to the FTMS was also proposed,that is the inclusion of a barrier to avoid the escape of polyhedron of the search region bounded by the upper and lower limits of the variables.

The numerical results demonstrated that MFTMS outperformed the standard FTMS for all the test functions investigated.Use of the Nelder–Mead algorithm with adaptive parameters was not an efficient strategy,although reasonable convergences could be achieved in some cases,notably for small dimensional problems.

The hybridization of the MFTMS with PSO(MFTMS-PSO)during initialization does not brought advantages in comparison with the FTMSPSO previously reported[8].

The barrier strategy applied in the MFTMS also proved to be efficient,mainly in the mass integration problems.Since a good range of variables are known in most real cases,this strategy prevents the flexible polyhedron from experiencing serious deformation during the minimization procedure.The success rate of MFTMS was 100%,while MFTMS-PSO achieved 85%,FTMAS 40%,and FTMA 30%.This demonstrates the improvement achieved using barrier in FTMS.The same strategy could be used in other optimization methods where the different amplitudes of variables make it hard to converge to an optimum.

The application of MFTMS in problems of mass integration was efficient to reach the optimum.Since from the current process con figuration,that often it is a local optimum,the method was able to found the global optimum,that is,the optimal process con figuration with integration mass issues satisfied.This class of problems was also solved with FTMS-PSO.However,as observed in Problem 1(maximization of the overall process yield),the results obtained with FTMS-PSO were not the globally known optima.The reason for this is that the particles generated led the optimization to be stuck in a region of local optima.With regard to the other two mass integration problems,the FTMS-PSO presented better performance than MFTMS,due to its ability to find the process optimum con figuration in a reasonable number of iterations and objective function evaluations.

The results found in this article brings an important conclusion because complex problems(as mass integration),usually solved with indirect methods,could be solved with a simple direct method improved,the MFTMS,and with an hybrid method,FTMS-PSO.Thus,problems that usually require a large preparation time,with derivatives calculus,can be easily and quickly solved without gradient calculations.

Acknowledgments

The authors thank CAPES(Coordenação de Aperfeiçoamento de Pessoal de Nível Superior)and CNPq (Conselho Nacional de Desenvolvimento Científico e Tecnológico,grant number 161464/2013-0)for financial support.

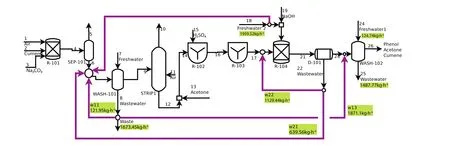
Fig.14.Optimized process flowsheet of the production of phenol from cumene hydroperoxide,Problem 3.

Fig.15.Source-sink representation of Problem 3.

Table 7Main results for Problem 2.N it:number of iterations,N eval:number of objective function evaluations

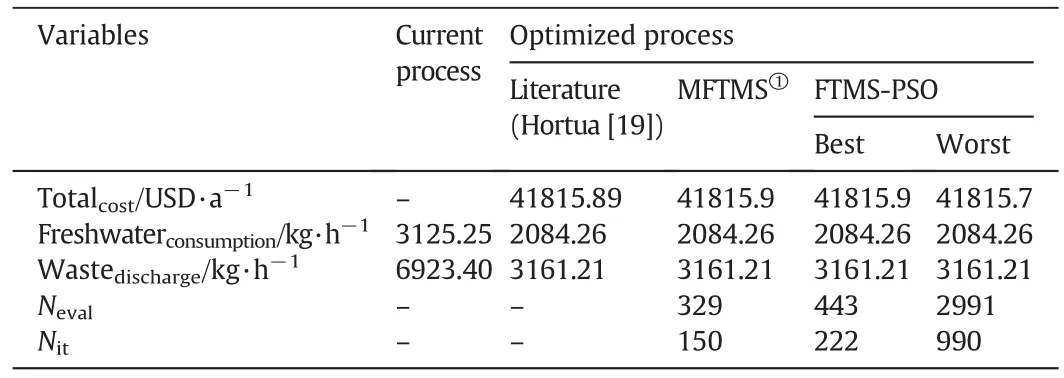
T able 8Main results for Problem 3.N it:number of iterations,N eval:number of objective function evaluations

[1]D.Paviani,D.Himmelblau,Constrained nonlinear optimization by heuristic programming,Oper.Res.17(5)(1969)872–882.

[2]P.Zhang,Y.Ren,Flexible tolerance simplex method and its application to multicomponent spectrophotometric determinations,Anal.Chim.Acta222(1)(1989)323–333.

[3]D.Constantinescu,Smooth and time-optimal trajectory planning for industrial manipulators along specified paths,J.Robot.Syst.17(2000)223–249.

[4]W.Shang,S.Zhao,Y.Shen,A flexible tolerance genetic algorithm for optimal problems with nonlinear equality constraints,Adv.Eng.Inform.23(3)(2009)253–264.

[5]S.Omowunmi,A.Susu,Application of tikhonov regularization technique to the kinetic data of an autocatalytic reaction:Pyrolysis of n-eicosane,Engineering3(2011)1161–1170.

[6]M.Naish,Sensing-system planning for the surveillance of moving objects(Ph.D.thesis)Department of Mechanical and Industrial Engineering,University of Toronto,2004.

[7]A.Lima,W.Kwong,A.Cruz,Comparative study and application of the flexible tolerance method in synthesis and analysis of processes with mass integration,J.Chem.Chem.Eng.7(3)(2013)228–238.

[8]A.Lima,W.Kwong,A.Cruz,Nonlinear constrained optimization using the flexible tolerance method hybridized with different unconstrained methods,Chin.J.Chem.Eng.25(4)(2017)442–452.

[9]D.Himmelblau,Applied nonlinear programming,McGraw-Hill,1972.

[10]F.Gao,L.Han,Implementing the Nelder–Mead simplex algorithm with adaptive parameters,Comput.Optim.Appl.51(1)(2012)259–277.

[11]J.Liang,T.Runarsson,E.Mezura-Montes,M.Clerc,P.Suganthan,C.Coello,K.Deb,Problem de finitions and evaluation criteria for the cec 2006 special session on constrained real-parameter optimization,Tech.Rep,Nangyang Technological University,Singapore,2006.

[12]S.Deb,K.Srivastava,A genetic algorithm based augmented lagrangian method for constrained optimization,Comput.Optim.Appl.53(3)(2012)869–902.

[13]S.Koziel,Z.Michalewicz,Evolutionary algorithms,homomorphous mappings,and constrained parameter optimization,Evol.Comput.7(1)(1999)19–44.

[14]J.Liang,P.Suganthan,Comparison of results on the 2006 cec benchmark function set,http://web.mysites.ntu.edu.sg/epnsugan/PublicSite/Shared 2006.

[15]R.Smith,Chemical process:Design and integration,Wiley,2005.

[16]M.El-Halwagi,Process Integration,Process Systems Engineering,Elsevier Science,2006.

[17]M.El-Halwagi,Pollution Prevention Through Process Integration:Systematic Design Tools,Elsevier Science,1997.

[18]M.Al-Otaibi,M.El-Halwagi,Targeting techniques for enhancing process yield,Chem.Eng.Res.Des.84(10)(2006)943–951.

[19]A.Hortua,Chemical process optimization and pollution preventionviamass and property integration,Master's thesis,Texas A&M University,2007.