刘志红（郑州财经学院计算机系，郑州450044）



具线性退化特征拟线性双曲型方程组的边值问题

刘志红
（郑州财经学院计算机系，郑州450044）

摘 要：研究如下的一阶拟线性双曲型方程组具有耗散型线性退化特征的情形下，其边值问题经典解的整体存在性，以及当t→∞时解的渐近性态，最后把结论应用到两个实际问题中。

关键词：线性退化特征；整体经典解；边值问题；拟线性双曲型方程组

0　引言

拟线性双曲型方程组是偏微分方程研究领域的一个重要组成部分。当前，研究结果比较成熟的是关于拟线性双曲方程组Cauchy问题研究［1－4］，但是对于其边值问题的研究，相对来说就比较少了［5－7］，尚未形成一般的理论。在大量的实际问题中，特别是在空气动力学、流体力学、非线性弹性力学、水力学等领域，经常会提出具有两个自变量的一阶拟线性双曲方程组的边值问题［8－10］。因此，对一阶拟线性双曲方程组边值问题的研究具有重要的理论意义和实际应用价值。

一般说来，拟线性双曲型方程组的边值问题在t≥0上并不存在整体经典解，这主要是因为边界数据的存在，造成在边界上反射波的强度可能会大于入射波的强度，或者在边界上有波的连续反射现象发生，但对于特殊的边界情况则不同。

于具（严格）对角占优矩阵的拟线性双曲型方程组，有如下结果：

（1）李大潜等人［7－8］在考虑一般的具内部耗散对角型主部的非齐次拟线性严格双曲型方程组的Cauchy问题时，证明了如果矩阵A是行（列）对角占优矩阵且主对角线上元素均相等，则当初值的C1模充分小时，Cauchy问题在t≥0存在唯一的整体经典解。

（2）对一般的非齐次拟线性严格双曲型方程组的Cauchy问题，肖玲、李大潜、秦铁虎等人［2－3，9－10］证明：若假设A是严格对角占优的，则当初值的C1模充分小时，Cauchy问题在t≥0存在唯一的整体经典解，且解的C1模当t→＋∞时依指数衰减到零。

（3）刘法贵［6］在考虑具耗散项一阶拟线性双曲型方程组的具有自由边界的典型自由边值问题，在A是严格对角占优的和真正非线性特征的情形，证明了其经典解的整体存在性定理。

本文考虑具耗散项一阶拟线性双曲型方程组边值问题，假设A是对角占优的和线性退化特征情形下，证明其经典解的整体存在性定理。

1　研究问题

讨论具耗散项线性退化拟线性双曲型方程组（*）式在如下边界的经典解问题：其中u＝（u1，…，un）T关于变量t和x的未知向量函数，A（u）＝（aij）n是关于变量u的具有适当光滑元的n ×n阶矩阵，g（u）是关于变量u的n维列向量函数。

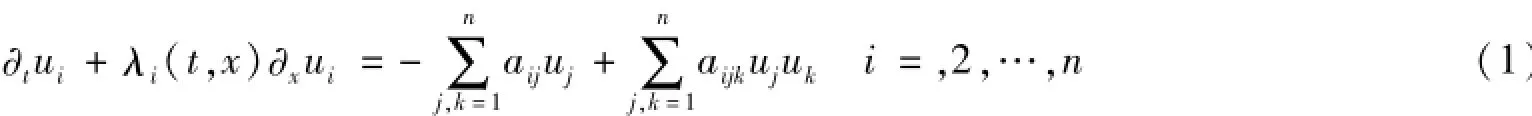
在D＝｛（t，x）｜t≥0，x1（t）≤x（t）≤x2（t）｝上具如下典型边值问题：

在光滑边界x＝x1（t）（x1（0）＝0）上：

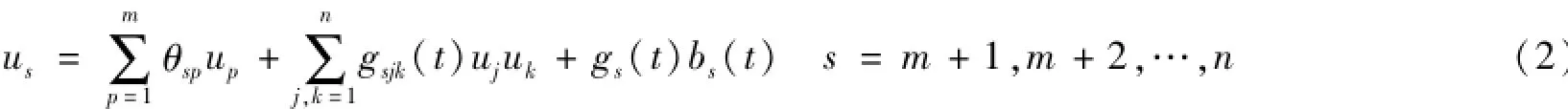
在光滑边界x＝x2（t）（x2（0）＝0）上：

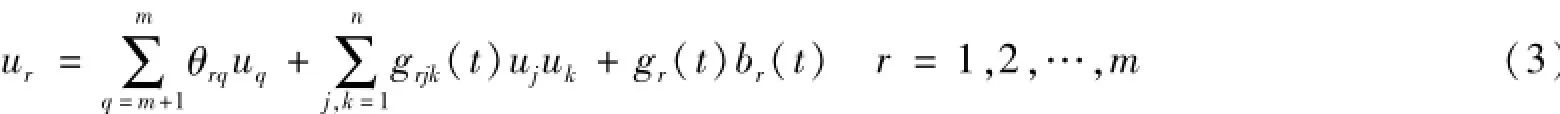
这里

假设：（H1） λi，θijk，θij，gijk，gi，Fl是适当光滑的函数，且在t≥0上保持有界；（H2） 边界条件（2）－（3）式存在唯一的解u≡u0（不失一般性，设u0＝0）；（H3） 过原点的特征线不进入区域D，即λr（0）≤F1（0）≤F2（0）≤λs（0）。令，则得到如下不等式：（H4） A＝L（0）▽g（0）L－1（0）＝（aij）是对角占优的。

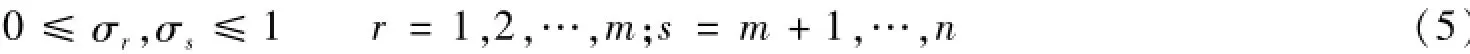
定理1 在上述假设（H1）－（H4）之下，如果存在充分小的ε＞0，使

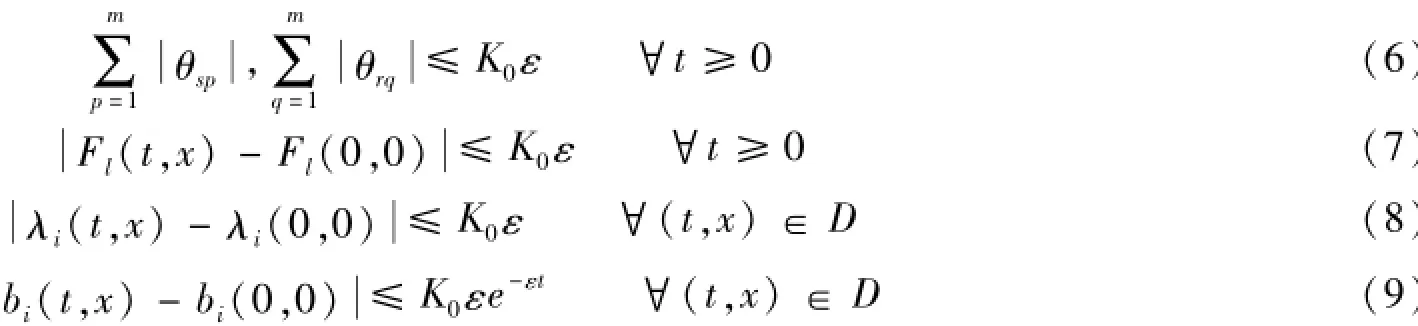
其中r＝1，2，…，m；s＝m＋1，…，n；i＝1，2，…，n；l＝1，2，这里及以后出现的K如无特殊说明均为不依赖于ε的正常数。则在典型边值问题（1）－（3）经典解u＝u（t，x）的存在区域上有

2　引理与解的一致先验估计

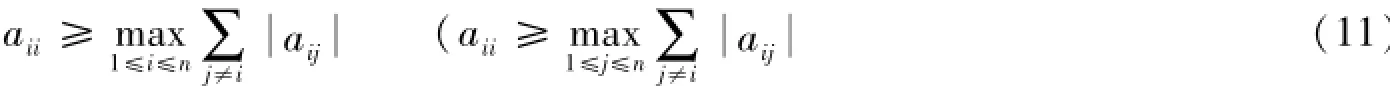
由文献［11］，得下面引理：

引理1 若A是行（列）严格对角占优矩阵，即A满足（11）式，则δ＞0，使得A的所有特征根λ*i，成立：

注记1 （12）式中引入的“δ”即为定理1中方程组经典解的指数衰减因子。

2.2 一致先验估计

我们对定理1的证明需要用到局部延拓法加一致先验估计的方法，因而这里我们先对解进行一致先验估计：

由（2）－（3），（9），并注意到u＝u（t，x）的连续性，在经典解存在区域D（σ）＝｛（t，x）0≤t≤σ，x1（t）≤x（t）≤x2（t）｝上，有

2.1 对角占优矩阵

本节主要讨论上文中提到的对角占优及严格对角占优（Strictly Diagonally Dominant）矩阵的相关引理和定理，以及在偏微分方程中的应用（指数衰减因子）。

定义1 矩阵A＝（aij）是行（列）对角占优矩阵，如果

因此，为了得到（10），只须证可以选择适当大的不依赖于ε的正常数K，若（t，x）∈D，有

则必有

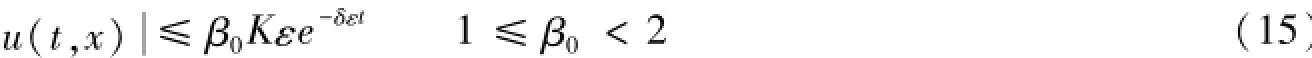
由于在推导这个先验估计时，已假设经典解存在，原来的未知自由边界曲线实际上为已知的边界曲线。

由（7）－（8）及（H3），如果ε＞0充分小，则

在x＝x1（t）上：

在x＝x2（t）上：

其中r＝1，2，…，m；s＝m＋1，…，n。

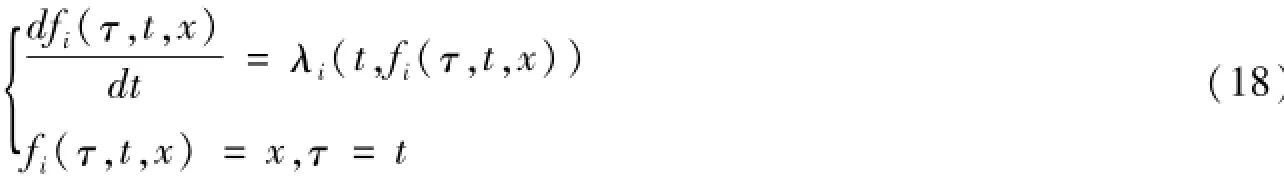
设ξ＝fs（τ，t，x）交边界x＝x1（t）于点（τs，x1（τs））向下引第s特征交边界x＝x2（t）于点（τsr，x2（τsr））；

设ξ＝fr（τ，t，x）交边界x＝x2（t）于点（τr，x1（τr））向下引第r特征交边界x＝x1（t）于点（τrs，x2（τrs））；

则由（4），有

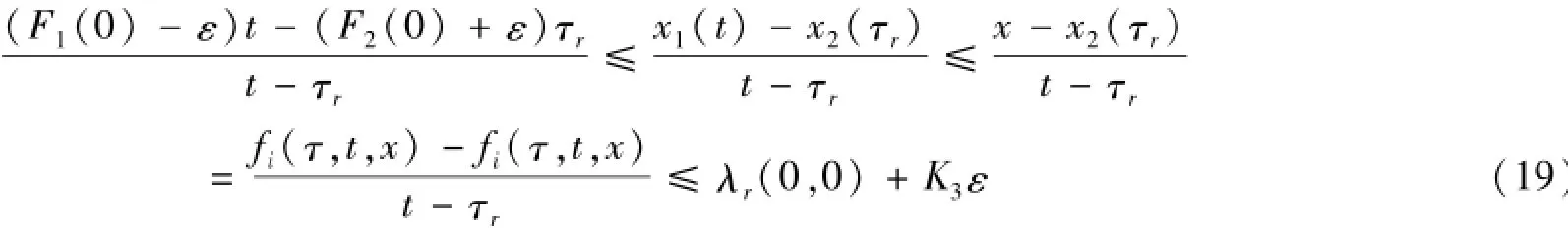
由此，得

即

进而

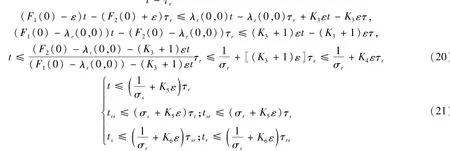
同理，有

这样，由（19）－（21），存在1＜β＜2，并能选择T＞0，使得

若ε＞0适当小，则

沿第r特征从（τr，x2（τr））到（t，x）积分（1）的第r个方程，并注意到（13），得

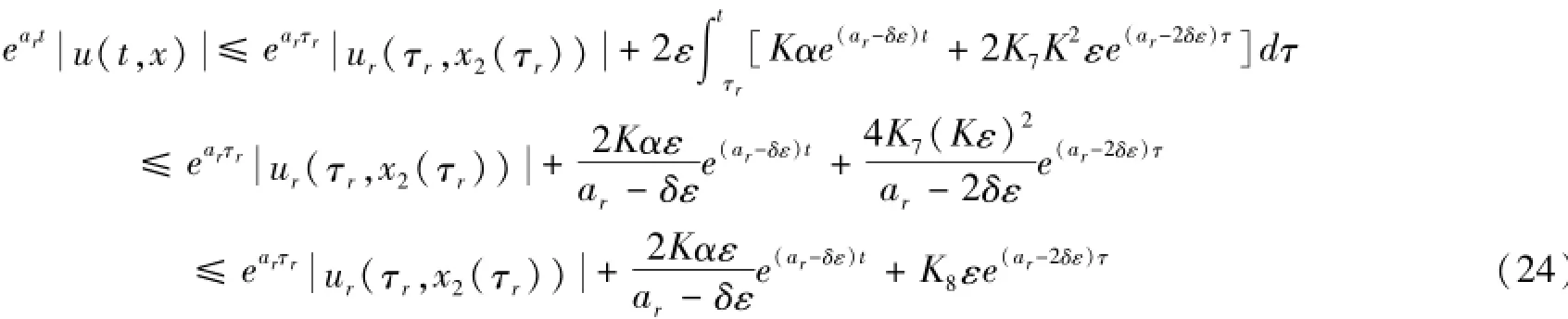
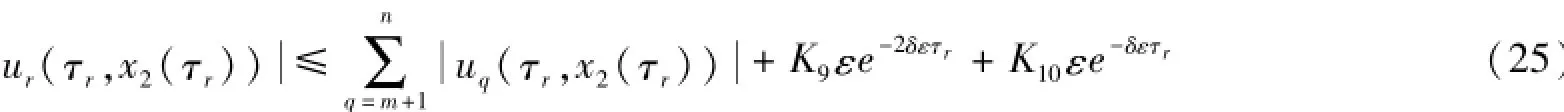
这样沿第s特征从（τrs，x2（τrs）到（τr，x2（τr））积分（1）的第s个方程，并注意到（24），得

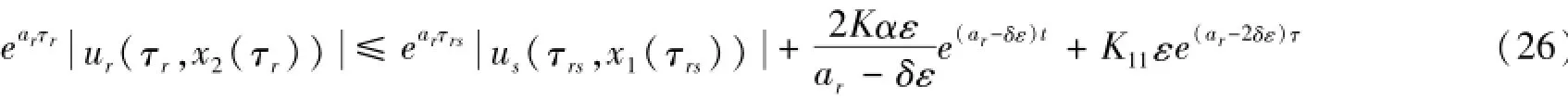
由（2），（11），（14），（20），得

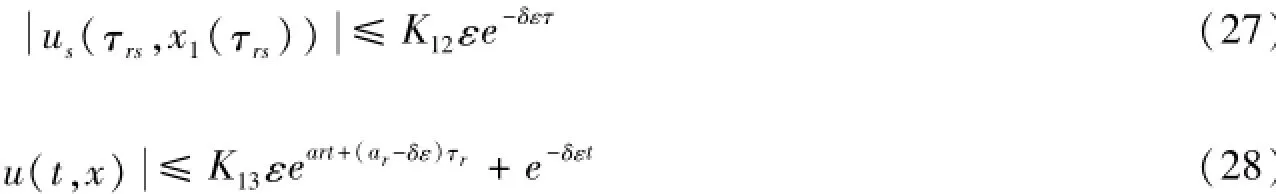
从而（24）式可化为

考虑上面不等式右边第二项，由（22）与（23），有

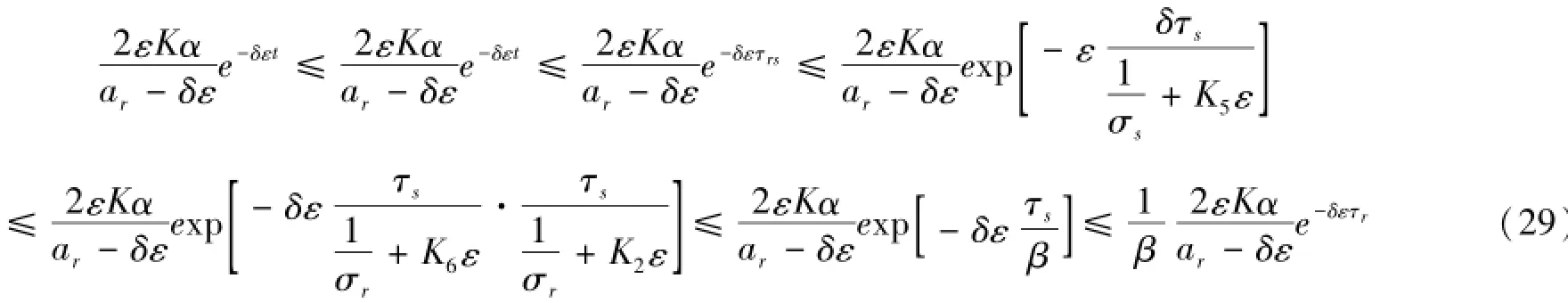
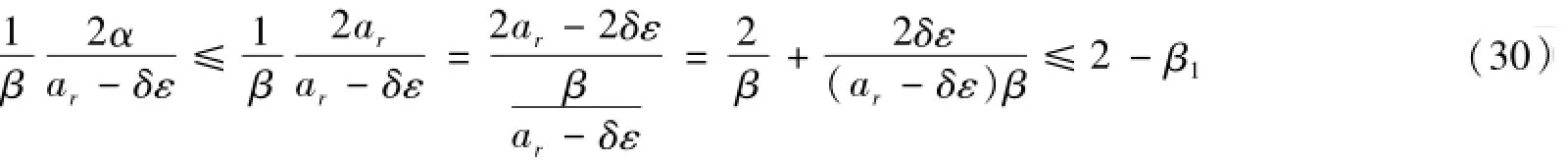
则（29）化为

由（28）－（31），得

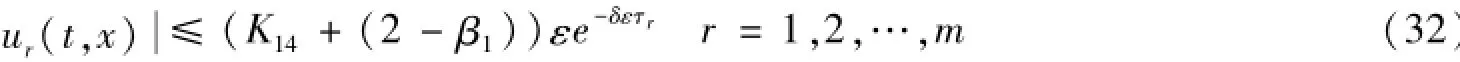
类似地，对于us（t，x）（s＝m＋1，…，n）有相仿于（32）的结论。因此，取（β0＋（β1－2））K≥K14，则一致先验估计式（21）成立。

3　主要定理的证明

定理1 证明：根据拟线性双曲型方程组边值问题经典解的局部存在唯一性定理［8］，典型边值问题（1）－（3）在区域（其中σ为适当小的常数）

D（σ）＝｛（t，x）｜0≤t≤σ，x1（t）≤x（t）≤x2（t）｝上存在唯一经典解u＝u（t，x）。

由2.2节一致先验估计，知可以选择适当大的不依赖于ε的正常数K。

由u（t，x）≤2Kεe－δεt，（t，x）∈D，则u（t，x）≤β0Kεe－δεt，1≤β0≤2，根据局部延拓法，即证得定理1，

定理1证毕。

4　定理的实际应用

考虑如下非等熵流体动力学方程组：

其中u，v，p＝p（v，s），s分别代表气体的速度、比容、压强和熵，v0（x）＝v（0，x）＞0满足

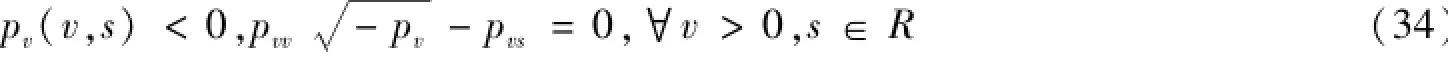
上式的第一条件，即pv（v，s）＜0保证方程组（33）是双曲的，后一个条件，即pvv槡－pv－pvs＝0保证方程组（33）是线性退化的。事实上，

容易计算得

注记2 式（40）的条件可以找到相应函数满足，例如：（其中C为常数）

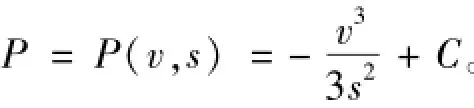
在D＝｛（t，x）t≥0，x1（t）≤x（t）≤x2（t ）｝上考虑，由（33）第三式及（34），可得s（t，x）＝s（x）s0（x）为了方便起见，在这里，将考虑如下的p（v，s（x）），即

p（v，s（x））＝kv－γes0k＞0，1＜γ＜3这样，（33）可以化为如下形式：

考虑（34）具如下的边值问题：

在光滑边界x＝x1（t）（x1（0）＝0）上：

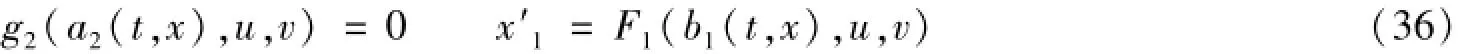
在光滑边界x＝x2（t）（x2（0）＝0）上：

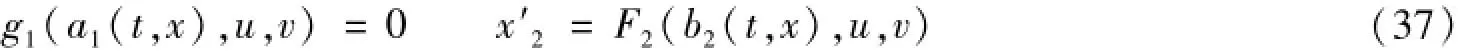
结论1 由定理1，可知此边值问题整体经典解存在。

表明，初始时刻没有真空态；而在经典解存在区域上，真空态永远不会出现。

结论2 从上述分析，易得式（38）表明：在边值问题（35）－（37）经典解的存在区域上，真空态永远不会出现.

注记3 在等熵情形下（即s≡常数），可以相应地给出具耗散项的边值问题经典解的存在性结果。

参考文献：

［1］刘法贵.具线性退化特征拟线性双曲型方程组的Cauchy问题［J］.华北水利水电学院学报：自然科学版，1999（4）.

［2］刘法贵.拟线性双曲型方程组Cauchy问题［M］.英文版.郑州：黄河水利出版社，2006.

［3］孔德兴.一阶拟线性双曲型方程组的Cauchy问题［J］.复旦学报：自然科学版，1994（6）.

［4］Liu Fagui，Yang Qiao.Cauchy Problem for Quasilinear Hyperbolic Systems with Weakenly Dissipative Terms［J］.Quart.J.of Math.，1994（3）.

［5］赵彦淳.一阶拟线性双曲型方程组的边值问题［J］.数学年刊A辑：中文版，1986（6）.

［6］刘法贵.具耗散项拟线性双曲型方程组的边值问题［J］.数学学报，1999（5）.

［7］Li Tatsien，Yu Wenci.Boundary Value Problem for Quasilinear Hyperbolic Systems［M］.Duke University Mathematics V，1985.

［8］刘存明.一阶拟线性双曲型方程组经典解的整体存在性及破裂机制［D］.上海：复旦大学，2012.

［9］Greenberg J M，Li Tatsien.The Effect of Boundary Damping for the Quasilinear Wave Equation，J.of Diff［J］.Equations，1984 （52）：66－75.

［10］Liu Taiping.Initial Boundary Value Problem for Gas Dynamics［J］.Arch.Rat.Mech.Anal.，1977（64）：137－168.

［11］刘志红.对角占优矩阵在偏微分方程中的应用［J］.河南教育学院学报：自然科学版，2014（4）.

（责任编辑 赵冰）

Boundary Value Problem for Quasilinear Hyperbolic Linera Degeneracy Systems

LIU Zhi－hong
（Department of Computer Science，Zhengzhou Institute of Finance And Economics，Zhengzhou 450044，China）

Abstract：In this paper，we study the following first－order quasilinear hyperbolic systems

We consider the boundary value problem of the hyperbolic systems（*）with Linearly Degenerate Type for the global existence of the classical solution，the asymptotic behavior of the solution as t→＋∞.

Key words：linearly degenerate characteristic；global classical solution；boundary value problem；quasilinear hyperbolic systems

作者简介：刘志红（1983—），男，河北邯郸人，郑州财经学院计算机系讲师。

基金项目：河南省高等学校重点科研项目计划（15B110010）

收稿日期：2015－07－10

文章编号：1008－3715（2015）05－0112－05

文献标识码：A

中图分类号：O175

DOI：10.13783／j.cnki.cn41－1275／g4.2015.05.023