曹萌

Bezoutian矩阵的一致逼近形式

曹萌

(安徽大学数学科学学院,安徽合肥230601)

借助闭区间上的连续函数可以用Bernstein多项式一致逼近这一事实,将多项式对所生成的经典Bezoutian矩阵和Bernstein Bezoutian矩阵推广到C[0,1]上函数对所对应的情形,给出了Bezoutian矩阵一致逼近形式的定义,并且得到如下结论:给出了经典Bezoutian矩阵的Barnett型分解公式和三角分解公式的一致逼近形式;提供了经典Bezoutian矩阵和Bernstein Bezoutian矩阵的一致逼近形式的两类算法;得到了上述两种矩阵的一致逼近形式中元素间的两个恒等关系式.最后,利用数值实例对恒等关系式进行验证,结果表明两类算法是有效的.

Bernstein多项式;经典Bezoutian矩阵;Bernstein Bezoutian矩阵;一致逼近形式;算法

1 引言

Bezoutian矩阵是一类由两个多项式所生成的特殊结构方阵,在控制理论、多项式稳定性理论等领域中发挥着重要作用[12],也是矩阵理论的一个热门研究方向(见文献[3-9]).另一方面,由于Bernstein多项式自身的优良性质,使得它在计算机辅助几何设计(CAGD)和计算机图形学(CG)中具有广泛的应用[1011].此外,对于由Bernstein多项式所衍生的如Bernstein型算子的研究也受到了科研工作者们的高度重视[1214].

考虑到闭区间上的连续函数可以用Bernstein多项式进行一致逼近这一重要性质,本文将函数逼近论思想应用到矩阵理论中来,对多项式对所生成的经典Bezoutian矩阵和Bernstein Bezoutian矩阵进行了推广,给出了C[0,1]上函数对所生成的Bezoutian矩阵的一致逼近形式的定义.在得出一些自身性质的同时,也为丰富和发展Bezoutian矩阵与友矩阵的缠绕关系、Bezoutian矩阵经Vandermonde矩阵合同后的对角约化以及Bernstein多项式的最大公因式的计算等问题[1517]起着参考作用,具有一定的实际意义.

本文具体安排如下:为了叙述的方便,第二节首先给出一些需要用到的相关定义;第三节给出了经典Bezoutian矩阵的Barnett型分解公式和三角分解公式的一致逼近形式;第四节给出了关于经典Bezoutian矩阵和Bernstein Bezoutian矩阵的一致逼近形式的两类算法;第五节得到了经典Bezoutian矩阵与Bernstein Bezoutian矩阵的一致逼近形式中元素间的两个恒等关系式.在最后一节中,通过数值实例对第五节提供的恒等关系式进行检验,结果表明所给的两类算法是有效可行的.

2 预备知识

定义2.1[18]对于给定的多项式对

称由多项式

所定义的矩阵为p(x)和q(x)在标准幂基{1,x,···,xn−1}下的经典Bezoutian矩阵;称由多项式

下的Bernstein Bezoutian矩阵.这里

定义2.2[19]设f(x)是C[0,1]上的函数,称

为f(x)的第n个Bernstein多项式.

定义2.3[19]设f(x)是C[0,1]上的函数,如果对于任意的ε>0,存在多项式P(x),使得对于任意x∈[0,1],总有|f(x)−P(x)|<ε成立,则称f(x)在[0,1]上可以用多项式一致逼近.

3 经典Bezoutian矩阵的Barnett型分解公式和三角分解公式的一致逼近形式

引理3.1[19]设f(x)是C[0,1]上的函数,那么∀ε>0,∃N>0使得n>N时,∀x∈[0,1]都有|Bn(f;x)−f(x)|<ε成立,即

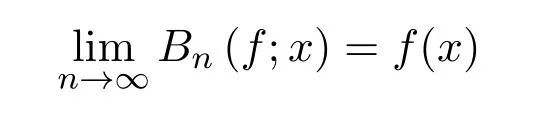
在[0,1]上一致成立.

定义3.1设f(x)和g(x)是C[0,1]上的函数对,则

和

在[0,1]上一致成立.称由函数

所定义的矩阵

为f(x)和g(x)在标准幂基{1,x,···,xn−1}下的经典Bezoutian矩阵的一致逼近形式;称由函数

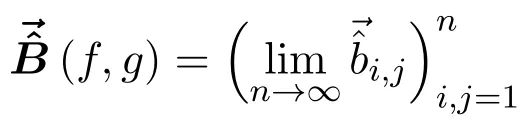
所定义的矩阵

引理3.2[19]

这里∆i称为i阶差分算子,∆µi=µi+1−µi,i=0,1,···,n−1.

引理3.3[20]对于给定的多项式对

称为p(x)的对称化子,

称为p(x)的第一酉矩阵.

定理3.1设f(x)和g(x)是C[0,1]上的函数对,则其中

分别称为C[0,1]上函数f(x)的对称化子和第一酉矩阵的一致逼近形式.

证明首先由引理3.2可知

再由定义3.1及引理3.3易知定理3.1成立.

引理3.4[21]对于给定的多项式对

即经典Bezoutian矩阵的三角分解公式.

定理3.2设f(x)和g(x)是C[0,1]上的函数对,则(f,g)

证明首先由引理3.2可知,

再由定义3.1及引理3.4易知定理3.2成立.

4 经典Bezoutian矩阵和Bernstein Bezoutian矩阵的一致逼近形式的算法

定理4.1C[0,1]上的函数对f(x)和g(x)在标准幂基{1,x,···,xn−1}下的经典Bezoutian矩阵的一致逼近形式

的算法如下:

证明由题设条件可知,

由引理3.2可知,

从而有

分别比较上式等号两端xi,xiyj以及xnyj的系数可知,

即可得出(1)-(3)式,故定理4.1成立.

引理4.1[22]多项式对

在Bernstein基

下的Bernstein Bezoutian矩阵B(p,q)=的算法如下:

定理4.2C[0,1]上的函数对f(x)和g(x)在Bernstein基

下的Bernstein Bezoutian矩阵的一致逼近形式

的算法如下:

证明根据引理3.2及引理4.1易知定理4.2成立.

5 经典Bezoutian矩阵与Bernstein Bezoutian矩阵的一致逼近形式中元素间的恒等关系式

引理5.1[22]标准幂基{1,x,···,xn−1}和Bernstein基

之间满足关系式:

其中Hn−1=(hi,j)n i,j=1,满足

定理5.1设C[0,1]上的函数对f(x)和g(x)在标准幂基{1,x,···,xn−1}和Bernstein基

下的经典Bezoutian矩阵和Bernstein Bezoutian矩阵的一致逼近形式分别为

和

证明对于C[0,1]上的函数对f(x)和g(x),由引理5.1可知,

从而有,

再由(6)式易知,

再由(7)式易知,

即(5)式成立.从而定理5.1成立.

6 数值实例

例6.1给定C[0,1]上的函数对f(x)=ex,g(x)=ln(1+x),则称f(x)和g(x)可分别表示成:

为了方便起见,取i=3,j=1,则由定理4.1可知,

由引理3.2易得,

代入到(8)式中可得,

此外,有

根据定理4.2可得,

代入到(9)式等号右端,有

从而有

即满足(4)式,同理可知(5)式成立.

数值实例表明:定理4.1和定理4.2中的两类算法是有效可行的,它将定理3.1和定理3.2关于经典Bezoutian矩阵的一致逼近形式的求解具体细化到每一个元素中,为此无需根据Barnett型分解公式或三角分解公式去求解Bezoutian矩阵的某一特定元素,这将为计算带来极大的方便.

[1]Fuhrmann P A.A Polynomial Approach to Linear Algebra[M].New York:Springer-Verlag,1996.

[2]Barnett S.Polynomials and Linear Control Systems[M].New York:Springer-Verlag,1983.

[3]Yang Z H.Polynomial Bezoutian matrix with respect to a general basis[J].Linear Algebra and its Applications,2001,331:165-179.

[4]Yang Z H,Hu Y J.A generalized Bezoutian matrix with respect to a polynomial sequence of interpolatory type[J].IEEE Transactions on Automatic Control,2004,49(10):1783-1789.

[5]Wu H Z.Generalized polynomial Bezoutian with respect to a Jacobson chain basis over an arbitrary f i eld[J]. Linear Algebra and its Applications,2010,432(12):3351-3360.

[6]Yang Z H,Cui B F.On the Bezoutian matrix for Chebyshev polynomials[J].Applied Mathematics and Computation,2012,219:1183-1192.

[7]Rost K.Matrix representations of split Bezoutians[J].Linear Algebra and its Applications,2012,436:3904-3918.

[8]Ehrhardt T,Rost K.Resultant matrices and inversion of Bezoutians[J].Linear Algebra and its Applications, 2013,439(3):621-639.

[9]Belhaj S.Computing the polynomial remainder sequence via Bezout matrices[J].Journal of Computational and Applied Mathematics,2013,250:244-255.

[10]卢振泰,陈武凡.基于Bernstein多项式的数字图像分存[J].电路与系统学报,2009,14(4):17-20.

[11]严兰兰.带形状参数的Bernstein-Bezier曲面[J].计算机工程与科学,2014,36(2):317-324.

[12]程丽.Bernstein-Kantorovich算子线性组合同时逼近的正逆定理[J].纯粹数学与应用数学,2011,27(1):56-62.

[13]单锐,魏金侠,张雁.Bernstein算子矩阵法求高阶若奇异积分微分方程数值解[J].华侨大学学报, 2012,33(5):595-600.

[14]刘国芬.一类推广的Bernstein-Kantorovich算子的点态逼近[J].纯粹数学与应用数学,2014,30(1):32-39.

[15]Fiedler M,Ptak V.Bezoutians and intertwining matrices[J].Linear Algebra and its Applications,1987,86: 43-51.

[16]Chen G N,Yang Z H.Bezoutian representation via Vandermonde matrices[J].Linear Algebra and its Applications,1993,186:37-44.

[17]Winkler J R,Yang N.Resultant matrices and the computation of the degree of an approximate greatest common divisor of two inexact Bernstein basis polynomials[J].Computer Aided Geometric Design, 2013,30:410-429.

[18]Lancaster P,Tismenetsky M.The Theory of Matrices with Applications[M].2nd ed.New York:Springer-Verlag,1985.

[19]常庚哲,史济怀.数学分析教程[M].北京:高等教育出版社,2003.

[20]Barnett S.A note on the Bezoutian matrix[J].SIAM Journal on Applied Mathematics,1972,22(1):84-86. [21]Helmke U,Fuhrmann P A.Bezoutians[J].Linear Algebra and its Applications,1989,122-124:1039-1097.

[22]Bini D A,Gemignani L.Bernstein-Bezoutian matrices[J].Theoretical Computer Science,2004,315:319-333.

The uniform approximation form of Bezoutian matrix

Cao Meng
(School of Mathematical Science,Anhui University,Hefei230601,China)

Using the fact that Bernstein polynomial has the character of uniform approximation to continuous function on a closed interval,we generalize the classical Bezoutian matrix and Bernstein Bezoutian matrix generated by a pair of polynomials to functions on the closed interval.The def i nition on the uniform approximation of Bezoutian matrices is given.And we obtain some conclusions about them.Firstly the uniform approximation form of the Barnett type factorization and triangular factorization formulas of classical Bezoutian matrix are presented.Secondly the algorithms of the uniform approximation form with respect to the classical Bezoutian matrix and Bernstein Bezoutian matrix are provided.Furthermore,we obtain two identical relations on elements of the uniform approximation form relative to the two matrices mentioned before.Finally the numerical example is presented to verify the identical relation and show the ef f ectiveness of the algorithms.

Bernstein polynomial,classical Bezoutian matrix,Bernstein Bezoutian matrix,algorithm, uniform approximation form

O151.21

A

1008-5513(2014)06-0649-12

10.3969/j.issn.1008-5513.2014.06.015

2014-07-10.

曹萌(1991-),硕士生,研究方向：矩阵与算子理论.

2010 MSC:15A09