LIU Shi-he (刘士和), FAN Min (范敏), XUE Jiao (薛娇)

State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China, E-mail: shihe3086@163.com

The mechanical energy equation for total flow in open channels*

LIU Shi-he (刘士和), FAN Min (范敏), XUE Jiao (薛娇)

State Key Laboratory of Water Resources and Hydropower Engineering Science, Wuhan University, Wuhan 430072, China, E-mail: shihe3086@163.com

(Received June 30, 2013, Revised March 16, 2014)

The mechanical energy equation is a fundamental equation of a 1-D mathematical model in Hydraulics and Engineering Fluid Mechanics. This equation for the total flow used to be deduced by extending the Bernoulli’s equation for the ideal fluid in the streamline to a stream tube, and then revised by considering the viscous effect and integrated on the cross section. This derivation is not rigorous and the effect of turbulence is not considered. In this paper, the energy equation for the total flow is derived by using the Navier-Stokes equations in Fluid Mechanics, the results are as follows: (1) A new energy equation for steady channel flows of incompressible homogeneous liquid is obtained, which includes the variation of the turbulent kinetic energy along the channel, the formula for the mechanical energy loss of the total flow can be determined directly in the deduction process. (2) The theoretical solution of the velocity field for laminar flows in a rectangular open channel is obtained and the mechanical energy loss in the energy equation is calculated. The variations of the coefficient of the mechanical energy loss against the Reynolds number and the width-depth ratio are obtained. (3) The turbulent flow in a rectangular open channel is simulated using 3-D Reynolds averaged equations closed by the Reynolds stress model (RSM), and the variations of the coefficient of the mechanical energy loss against the Reynolds number and the width-depth ratio are discussed.

open channel, mechanical energy equation, steady flow, turbulent flow

Introduction

The continuity equation, the momentum equation and the mechanical energy equation of the total flow are the basis of the 1-D flow description in Hydraulics and Engineering Fluid Mechanics[1], and the mechanical energy equation is particularly a fundamental part. In the field of Fluid Mechanics, focuses are on the mechanism of the turbulent flow[2-5], the flow stability[6-8]and the related spatial or temporal distributions of the flow characteristics, studied by experiments or numerical simulations. For example, Abusbeaa and Shmela[9]conducted experiments over smooth channel beds with laser Doppler anemometer (LDA) to investigate the mean velocity distribution of uniform turbulent flows and compared these profiles with some available models. Nezu and Onitsuka[10]studied turbulent structures in partly vegetated open-channel flows with LDA and particle image velocimetry (PIV). Sanjou et al.[11]studied the turbulence structure incompound open-channel flows with one-line emergent vegetation by acoustic Doppler velocimeter (ADV). Dong and Zheng[12]studied spiral turbulence with direct numerical simulation (DNS). Chung and Pullin[13]investigated stationary buoyancy-driven turbulence with DNS and large-eddy simulation (LES). However, the energy equation and the mechanical energy loss were not well studied based on the fundamental theory in Hydraulics and Fluid Mechanics.

The energy equation for the total flow (the integral form of the energy equation) used to be deduced in the following manner in Hydraulics: (1) Constructing a stream tube around a stream line and extending the Bernoulli’s equation[1]for the ideal fluid along the stream line to the stream tube to obtain the energy equation for the stream tube. (2) Adding a term to consider the viscous effect in the energy equation for the stream tube, and integrating this equation in the cross section to obtain the energy equation for the total real fluid. The integration form of the adding term is called the energy loss (the mechanical energy loss) of the total flow which should be determined by experimental or observational data. This energy equa-tion is still being used. However, there are shortcomings from the point of hydrodynamics: (1) The variations of the turbulent kinetic energy along the main flow direction can not be described. (2) The assumption of a static pressure distribution at the cross section can not be justifiable for the 3-D turbulent flow since there exists secondary flows at the cross section. (3) The formula of the mechanical energy loss can not be determined directly. Although the transformation and the loss of the mechanical energy for steady incompressible pipe flows of homogeneous fluid were studied in Ref.[14], the energy equation for the total flow in the open channel has not be obtained yet. Therefore, in this paper, a new energy equation for steady incompressible channel flows of homogeneous liquid is derived to avoid the shortcomings mentioned above. In addition, the velocity distributions of steady laminar and turbulent flows in a rectangular channel are obtained analytically or numerically, and the mechanical energy loss in the energy equation is studied based on these results.

1. Formulation of the mechanical energy equation

In general, there are differences between the open-channel flow and the pipe flow, which may be summarized as follows: (1) The open-channel flow is a gravity-driven flow while the pipe flow may be driven by both the pressure difference and the gravity. (2) The boundaries of the pipe flow are solid boundaries, while there exist both solid boundaries and free surfaces in the open channel flow, with different boundary conditions. Consider the control volumeVin the open channel flow as shown in Fig.1. The surfaceAof the control volumeVis composed of two crosssections1A,A2at the upstream and the downstream with a distanceLbetween them, the channel wall and the free surface, and the angle betweenx1axis and the horizontal direction isθ. As shown in Fig.1, suppose that the equation for the free surface under the condition of a steady flow isη=η(x1,x2), the componentsniof the unit normal vector to the free surface pointing in the external direction are

Combining Eq.(1) with Eq.(2), we have 0 at the free surface for a steady flow. In addition, for the open channel flow, the velocity differences between the liquid and the air is usually not so large, and the curvature radius of the free surface is large enough that the effect of the surface tension can be ignored, therefore, we may assume that there is no shear stress on the free surface and the normal stress is just the atmosphere pressure.

The differential form of the (mechanical) energy equation for a steady flow of incompressible homogeneous liquid in the gravitational field can be obtained using the Navier-Stokes equations, which is

whereρis the liquid density andui,p,τij,sijare the velocity, the pressure, the viscous stress and the rate of deformation, respectively. The integral form of the energy equation for steady flows in laminar and turbulent states (corresponding to the statistical quantities in ensemble average) will be discussed below based on Eq.(3).

Fig.1 Sketch of open channel flow

1.1Laminar open channel flow

Integrating Eq.(3) over the control volumeVshown in Fig.1, and using the Gaussian Theorem to transform the volume integral into the surface integral for the left term and the first and third terms on the right hand side, we have

If there exists only the velocity componentu1(x2,x3) inx1direction on the two cross-sections1A,A2, then the potential energy (which is called the piezometric head in Hydraulics)gx3cosθ+p/ρon either 1AorA2is constant. By introducing the no-slip condition on the channel wall and the kinematical boundary condition that at the free surfaceujnj=0 we have

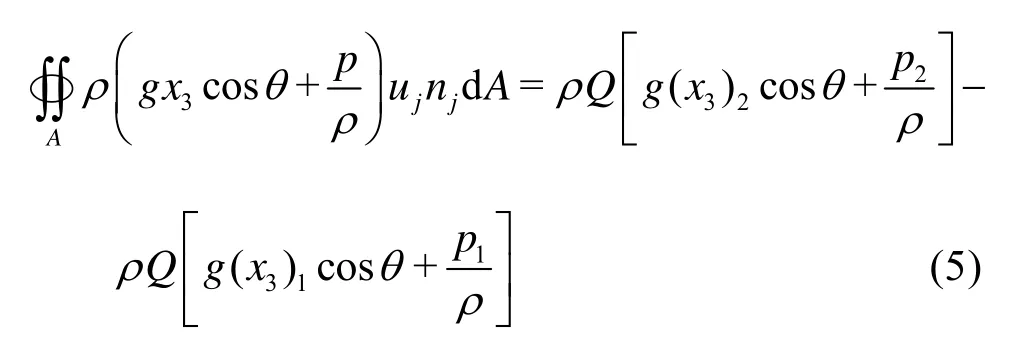
whereAis the cross-sectional area andQis the flow discharge in the section. The indexes 1 and 2 are used to represent the corresponding quantities at cross sectionsA1andA2. Define the kinetic energy correction coefficients1αand2αsuch that

whereUis the mean velocity in the section, and definehwas

wherezis the vertical coordinate, normal to the horizontal plane andz1-z2=(x3)1cosθ-(x3)2cosθ+Lsinθ.

It can be seen from Eq.(7) that a part of the mechanical energy is consumed owing to the viscous effect while the liquid flows from the cross section1AtoA2.

If the shapes and the sizes of cross sections1AandA2are identical, andτij,uihave the same distributions on these sections, we have

i.e., there is no mechanical energy transformation while the fluid flows from the cross section1AtoA2. In this case the mechanical energy loss per unit weight in unit time becomes

Furthermore, if the flow among cross sections 1AandA2is just a uniform flow, the mechanical energy loss per unit weight in unit time can be simplified further as

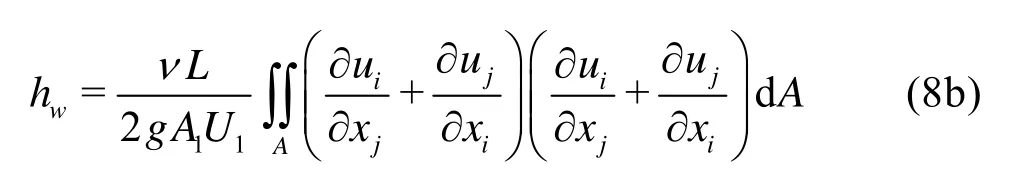
1.2Turbulent open channel flow

Applying the Reynolds decomposition to Eq.(3), then taking ensemble average, for a steady turbulent flow in the sense of ensemble averaged quantities we have:

Therefore Eq.(9) can be obtained by taking ensemble average

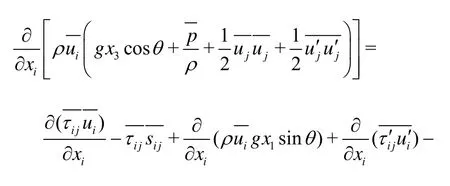
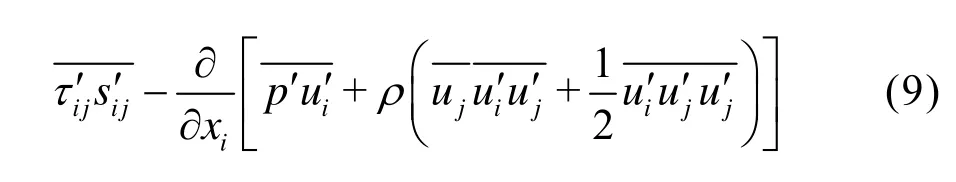
Integrating Eq.(9) over the control volumeV, and using the Gauss Theorem to transform the volume integral into the surface integral for the left term and the terms on the right hand side, we have

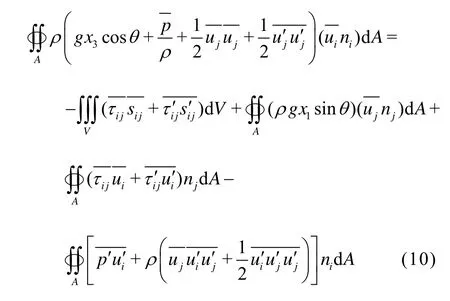
For a turbulent open channel flow, the assumption of a static pressure distribution at the cross sections can not be satisfied strictly owing to the presence of secondary flows at the cross sections. Usingpsto represent the hydrostatic pressure such thatgx3cosθ+ps/ρ=C, and usingρF1andρF2to represent the deviations between the hydrodynamic pressuresandand the hydrostatic pressuresps1andps2at the cross-sectionsA1andA2[1]we have:

Define the mean kinetic energy correction coefficients1α,2αand the turbulent kinetic energy correction coefficients1β,2βsuch that

Using the no-slip boundary condition on the channel wall, the kinematical boundary condition and the dynamical boundary condition at the free surface and the continuity condition for a steady flow, Eq.(10) can be simplified similar to Eq.(7) as

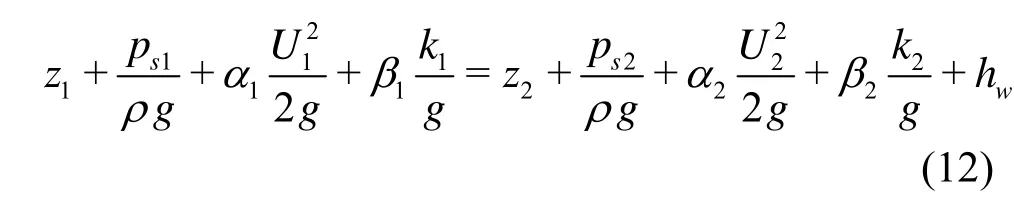
Equation (12) is the integral form of the energy equation for a steady turbulent open channel flow. In the equation,hwrepresents the mechanical energy transformation and loss between two cross sections per unit weight in unit time, which can be expresses as

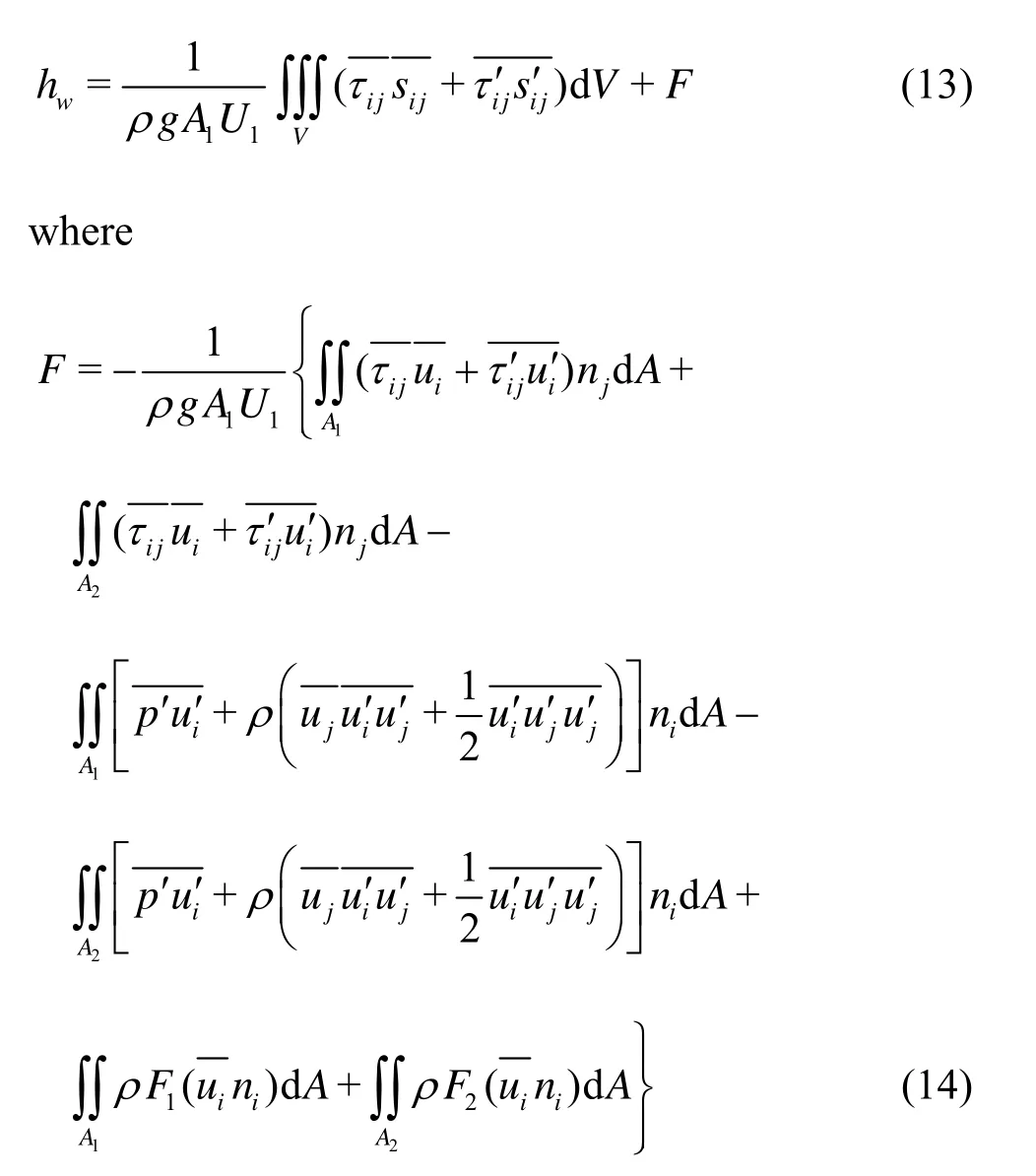
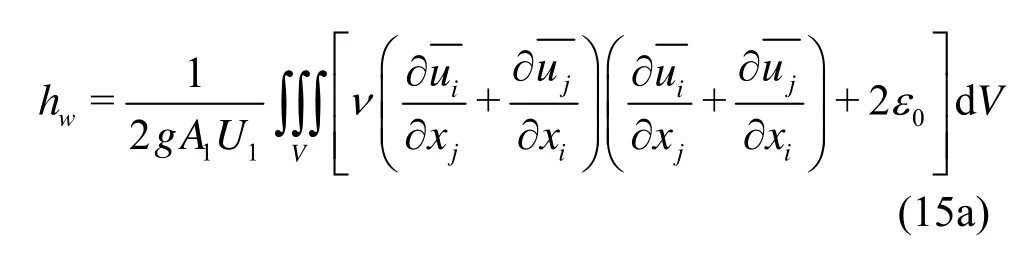
Furthermore, if the flow is uniform and the cross sections along the channel are identical, the mechanical energy loss between cross sections 1AandA2can be further simplified as

2. Laminar flow in an open channel with rectangular cross section

2.1Theoretical solution of the velocity field

The governing equation for the longitudinal velocityu1for a uniform laminar flow in a rectangular open channel of widthBand depthHcan be obtained by simplifying the Navier-Stokes equations, which is

By using the method of separation of variables to Eq.(16), we obtain

2.2Calculation of mechanical energy loss

The coefficientλof the mechanical energy loss for the total flow is defined as

ReURνis the Reynolds number which is characterized by the hydraulic radiusRand the mean velocityUin the section. Eq.(8b) can be simplified as

Equation (19) is just the Darcy-Weisbach formula for the laminar open channel flow. Combining Eq.(17) with Eq.(18), we have

In Fig.2 the variations ofλagainstReRandB/Hare given. It can be seen thatλdecreases with the increase ofReRfor a givenB/H, and increases with the increase ofB/Hfor a givenReR.

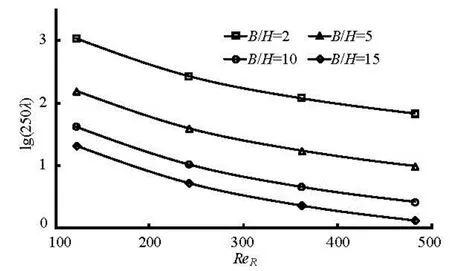
Fig.2 Variations ofλagainstReRandB/Hfor uniform laminar flow in rectangular open channel

In addition, the coefficient for a uniform laminar flow in a wide and shallow rectangular open channel is

Comparing Eq.(20) with Eq. (22), we have

In Fig.3 the relationship betweenf1andB/His given. It can be seen from Fig.3 that:f1decreases with the increase ofB/H, The value off1is always larger than 1 andf1decreases to 1.05 whileB/His larger than 350. Therefore, the rectangular open channel can be treated as a wide-shallow open channel in the laminar flow condition only ifB/H＞350 from the point of the mechanical energy loss.

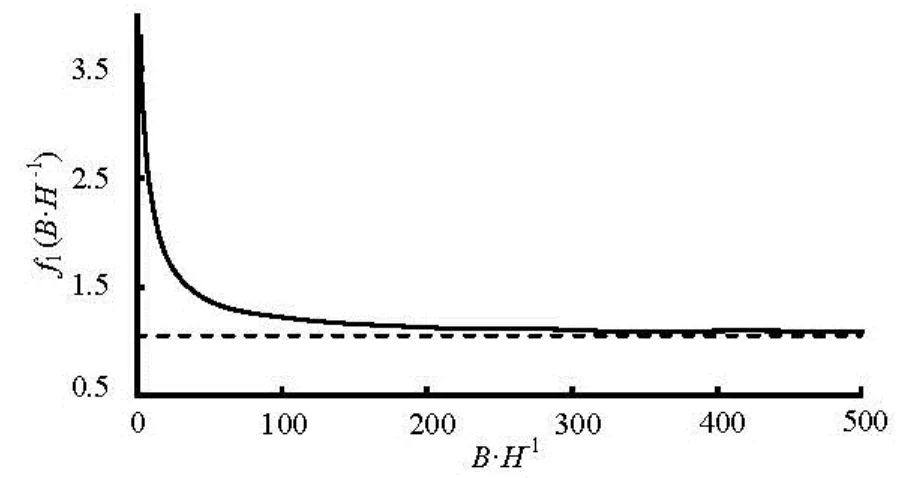
Fig.3 Variation off1againstB/H

3. Turbulent flow in the open channel with rectangular section

3.1Simulation of mean flow field for 3-D channel flow

3.1.1 Governing equations

The governing equations for a 3-D flow with RSM are as follows:

3.1.2 Boundary conditions

3.1.3 Numerical scheme

The 3-D turbulent flow in the rectangular open channel with the same hydraulic radius and the different width-depth ratios are simulated. The governing equations are discretized by the finite volume method (FVM) over the control volume, a first-order accuracy SIMPLE scheme is used for the convection term while the central difference scheme is used for the diffusion term. The variables are taken values at the center of the control volume and the collocated variable arrangement is employed to deal with the coupling relationship between the pressure and the velocity.

The algebraic equations are solved by the Gauss-Seidel iteration method in this paper. The converging criterion is that the unit mass flow residual should be less than 0.01% of the inflow and the overall mass flow residual should be less than 0.5% of the inflow.

3.1.4 Validation

The experimental results of Abubaker in Ref.[9] are used for validation. The experiments were performed in a glass walled open channel of 5.5 m long with cross section of 0.25 m×0.25 m and an adjustable bed slope. In Fig.4 the simulated velocity is compared with the experimental data. It can be seen from Fig.4 that the two results are in good agreement with each other.

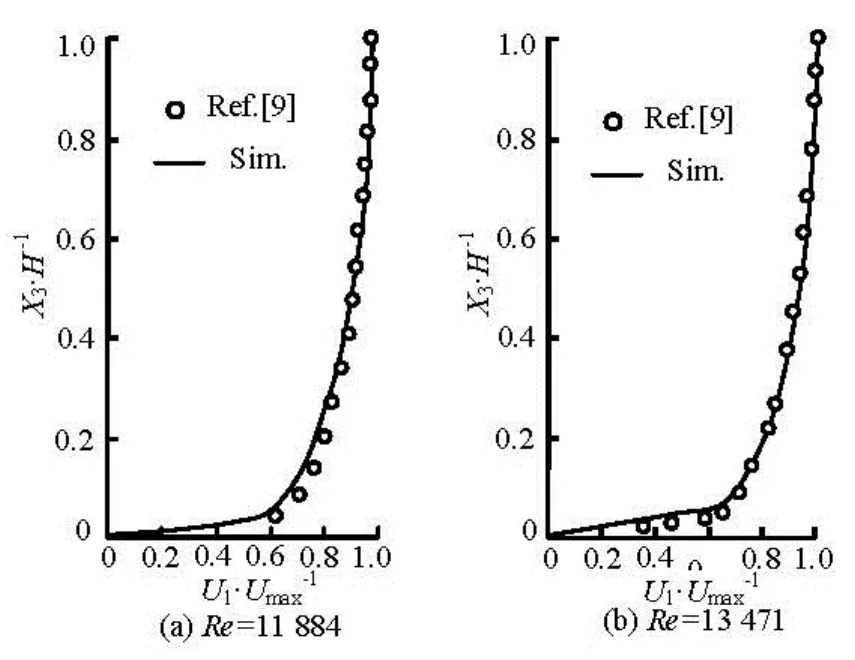
Fig.4 Comparison of calculated velocity distribution with experimental data

3.2Calculation of mechanical energy loss

For a uniform turbulent flow in an open channel, the total turbulent energy dissipation is equal to the total turbulent energy generation in cross section1A, i.e.,

Define the coefficient of the mechanical energy lossλas

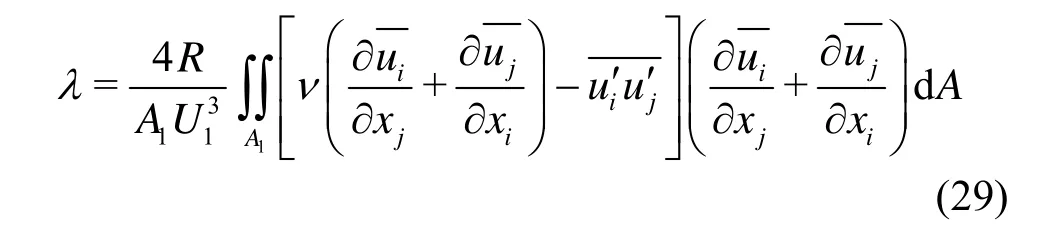
Then Eq.(15b) can be rewritten as

The formula is the same as the Darcy-Weisbach formula for an open channel flow exactly. Зегжда also gave an empirical expression betweenλandReRbased on experimental data as

In Fig.5 the variations ofλagainstReRandB/Hare given, based on Eq.(29) and the simulated results, and the comparison between the calculated results and Eq.(31) is given as well. It can be seen from Fig.5 that: (1)λvaries with both the Reynolds numberReRand the width-depth ratioB/H, whenReRis small,λvaries significantly withB/H, and the influence ofB/Honλdecreases with the increase ofReR. (2) The lower enveloping curve exists whenλvaries with the width-depth ratios for a given Reynolds number, and this agrees well with the existing empirical expression.

Fig.5 Variations ofλagainstReRandB/Hfor uniform turbulent flow in open channel

4. Conclusions

From the theoretical analyses and numerical simulations, the following conclutions are drawn.

(1) A new mechanical energy equation for the steady open channel flow of incompressible homogeneous liquid is obtained which includes the variation of the turbulent kinetic energy. The formula of the mechanical energy loss can be deduced directly from this energy equation.

(2) The theoretical solution of the velocity field for the laminar flow in a rectangular open channel is obtained and the variations of the coefficient of the mechanical energy loss against the Reynolds number and the width-depth ratio are obtained based on it.

(3) The 3-D turbulent flow in an open channel is simulated, and the variations of the coefficient of the mechanical energy loss against the Reynolds number and the width-depth ratio are discussed on the simulation results. A lower enveloping curve is found to exist while the coefficient of the mechanical energy loss varies with the width-depth ratio for a given Reynolds number.

[1] ZHANG Zhao-shun, CUI Gui-xia.Fluid mechanics[M].Second Edition, Beijing, China: Tsinghua University Press, 2006(in Chinese).

[2] LIU Shi-he, LIU Jiang and LUO Qiu-shi et al.Engineering turbulence[M]. Beijing, China: Science Press, 2011(in Chinese).

[3] EFROS V., KROGSTAD P.-A. Development of a turbulent boundary layer after a step from smooth to rough surface[J].Experiments in Fluids,2011, 51(6): 1563-1575.

[4] WANG X., SUN Y. Experimental study of the effects of roughness on the flow structure in a gravel-bed channel using particle image velocimetry[J].Journal of Hydrologic Engineering,2011, 16(9): 710-716.

[5] LANGHI M., HOSODA T. and DEY S. Velocity deformation model for unsteady open-channel flows over smooth and rough beds[J].Journal of Hydraulic Engineering, ASCE,2013, 139(4): 433-443.

[6] WANG Xin-jun, LUO Ji-sheng and ZHOU Heng. Mechanism of breakdown process of the laminar-turbulent transition in plane channel flow[J].Science in China, Series G: Physics, Mechanics and Astronomy,2005, 35(1): 71-78.

[7] GÜZEL B., BURGHELEA T. and FRIGAARD I. A. et al. Observation of laminar-turbulent transition of a yield stress fluid in Hagen-Poiseuille flow[J].Journal of Fluid Mechanics,2009, 627: 97-128.

[8] STOESSER T., RUETHER N. and OLSEN N. R. B. Calculation of primary and secondary flow and boundary shear stresses in a meandering channel[J].Advances in Water Resources,2010, 33(2): 158-170.

[9] ABUSBEAA A. M., SHMELA S. N. Velocity flow profiles over smooth bed in open channels[J].Journal of Engineering Research,2009, 9(12): 1-12.

[10] NEZU I., ONITSUKA K. Turbulent structures in partly vegetated open-channel flows with LDA and PIV measurements[J].Journal of Hydraulic Research,2001, 39(6): 629-642.

[11] SANJOU M., NEZU I. and SUZUKI S. et al. Turbulence structure of compound open-channel flows with one-line emergent vegetation[J].Journal of Hydrodynamics,2010, 22(5 Suppl.): 577-581.

[12] DONG S., ZHENG X. Direct numerical simulation of spiral turbulence[J].Journal of Fluid Mechanics,2011, 668: 150-173.

[13] CHUNG D., PULLIN D. I. Direct numerical simulation and large-eddy simulation of stationary buoyancy-driven turbulence[J].Journal of Fluid Mechanics,2010, 643: 279-308.

[14] LIU Shi-he, XUE Jiao and FAN Min. On the calculation of mechanical energy loss for steady pipe flow of homogenous incompressible fluid[J].Journal of Hydrodynamics,2013, 25(6): 912-918.

[15] LIU Shi-he, YIN Shu-ran. Study on turbulent flow around sand dunes in alluvial rivers[J].Journal of Hydrodynamics,2010, 22(1): 103-109.

10.1016/S1001-6058(14)60047-0

* Biography: LIU Shi-he (1962-), Male, Ph. D., Professor